Resolution of forces is the process of finding the components of a force. Let’s dive into more detailed explanation of resolution of forces.
If we tie a stone with a rope and pull it by making an angle $60°$ with the ground, then the stone moves horizontally. The force which causes the stone to move horizontally is smaller than the force applied because it is the resolved part of the force along the horizon. It is the horizontal component of the applied force $F$ and is denoted by $F_X$ or $X$.
The remaining part of the force lifts the stone vertically upwards, and is the resolved part of the force in the vertical direction. It is the vertical component of the applied force $F$ and is denoted by $F_Y$ or $Y$.
The process of finding the components of a force is known as the resolution of forces. This can be found by constructing a parallelogram with the line segment or vector representing the force as the principal diagonal. Since an infinite number of parallelograms can be drawn having same diagonal, so a force may be resolved into two components in an infinite number of ways in any two assigned directions.
Resolution of a given force into two components along two given directions
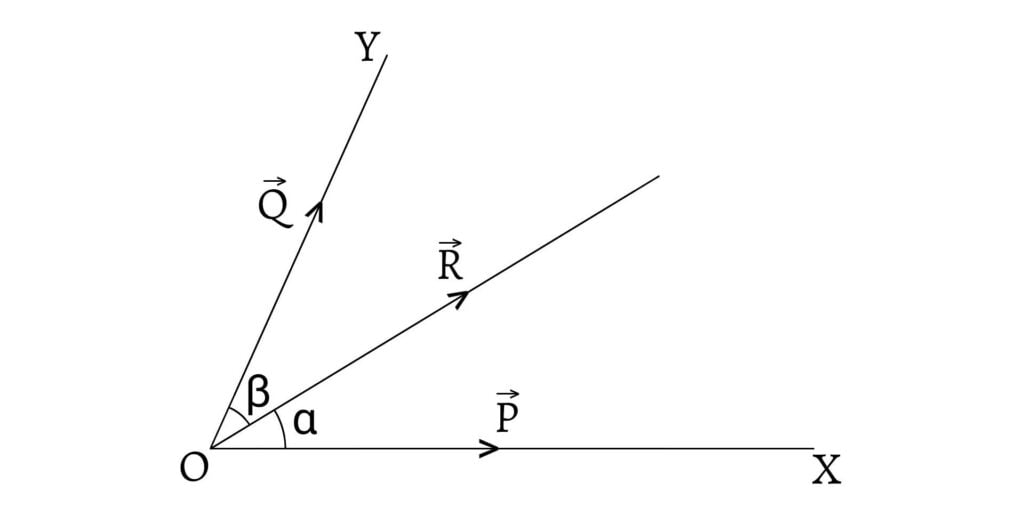
Let $R$ be the given force represented by $OC$. Now, we are going to resolve this force in two directions $OX$ and $OY$ making angles $\alpha$ and $\beta$ respectively with $OC$.

From $C$, draw $CA$ and $CB$ parallel to $YO$ and $XO$ respectively. Then $OACB$ is a parallelogram having $OC$ as its diagonal. Then, by parallelogram law of forces, $OA$ and $OB$ represent the components $P$ and $Q$ (say) having $R$ as their resultant. Since $AC$ and $OB$ are equal and parallel, $AC$ represents the same force $Q$.
Since the sides of the triangle $OAC$ are proportional to the sine of the opposite angles [Sine Law], we have
\[\frac{OA}{\sin OCA}=\frac{AC}{\sin COA}=\frac{OC}{\sin OAC}\] \[\frac{P}{\sin\beta}=\frac{Q}{\sin\alpha}=\frac{R}{\sin[π-(\alpha+\beta)]}\] \[\frac{P}{\sin\beta}=\frac{Q}{\sin\alpha}=\frac{R}{\sin(\alpha+\beta)}\] \[\therefore P=\frac{R\sin\beta}{\sin(\alpha+\beta)}\text{ and }Q=\frac{R\sin\alpha}{\sin(\alpha+\beta)}\]
Alternative Method
Let $\overrightarrow{R}$ be the given force which is to be resolved along $OX$ and $OY$ making angles $\alpha$ and $\beta$ respectively. Let $OX$ and $OY$ represent the two components of $\overrightarrow{R}$; $\overrightarrow{P}$ and $\overrightarrow{Q}$ respectively.
\[\overrightarrow{R}=\overrightarrow{P}+\overrightarrow{Q}\] \[\overrightarrow{P}×\overrightarrow{R}=\overrightarrow{P}×\overrightarrow{P}+\overrightarrow{P}×\overrightarrow{Q}\] \[\overrightarrow{P}×\overrightarrow{R}=\overrightarrow{P}×\overrightarrow{Q}\] \[|\overrightarrow{P}×\overrightarrow{R}|=|\overrightarrow{P}×\overrightarrow{Q}|\] \[PR\sin\alpha=PQ\sin(\alpha+\beta)\] \[\therefore Q=\frac{R\sin\alpha}{\sin(\alpha+\beta)}\]
Again, \[\overrightarrow{R}=\overrightarrow{P}+\overrightarrow{Q}\] \[\overrightarrow{R}×\overrightarrow{Q}=\overrightarrow{P}×\overrightarrow{Q}+\overrightarrow{Q}×\overrightarrow{Q}\] \[\overrightarrow{R}×\overrightarrow{Q}=\overrightarrow{P}×\overrightarrow{Q}\] \[|\overrightarrow{R}×\overrightarrow{Q}|=|\overrightarrow{P}×\overrightarrow{Q}|\] \[RQ\sin\beta=PQ\sin(\alpha+\beta)\] \[\therefore P=\frac{R\sin\beta}{\sin(\alpha+\beta)}\]
Resolve a force equal to $50N$ into two forces making angles of $60°$ and $45°$ with it.
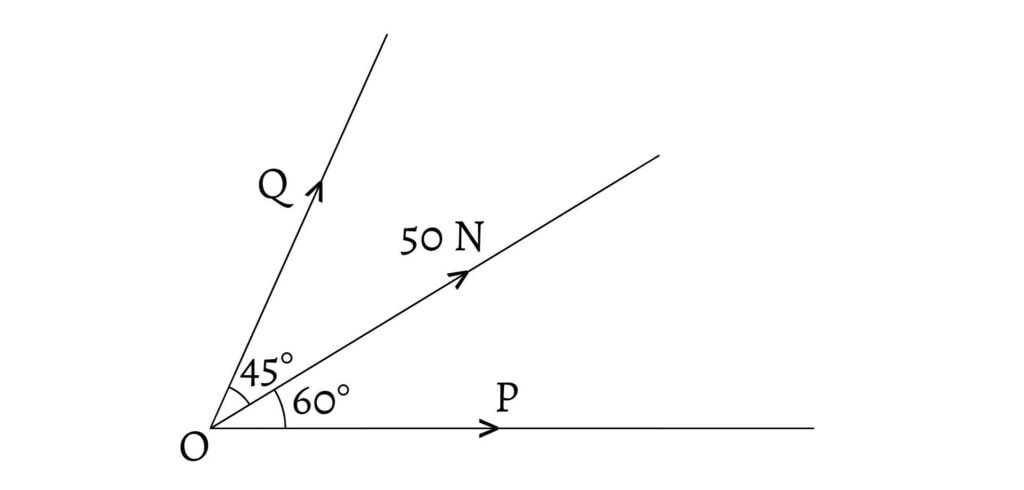
Let $P$ and $Q$ be the two forces making angle $60°$ and $45°$ respectively with $50N$ force. \[\therefore P=\frac{50×\sin45°}{\sin(60°+45°)}\] \[=\frac{50×\sin45°}{\sin60°\cos45°+\cos60°\sin45°}\] \[=\frac{50×\frac{1}{\sqrt{2}}}{\frac{\sqrt{3}}{2}×\frac{1}{\sqrt{2}}+\frac{1}{2}×\frac{1}{\sqrt{2}}}=\frac{\frac{50}{\sqrt{2}}}{\frac{\sqrt{3}+1}{2\sqrt{2}}}\] \[=\frac{100}{\sqrt{3}+1}=\frac{100(\sqrt{3}-1)}{(3-1)}\]\[=50(\sqrt{3}-1)N\]
\[\text{and, }Q=\frac{50×\sin60°}{\sin(60°+45°)}\] \[=\frac{50×\sin60°}{\sin60°\cos45°+\cos60°\sin45°}\] \[=\frac{50×\frac{\sqrt{3}}{2}}{\frac{\sqrt{3}+1}{2\sqrt{2}}}=\frac{50×\sqrt{6}}{\sqrt{3}+1}\] \[=\frac{50\sqrt{6}×(\sqrt{3}-1)}{3-1}\] \[=25(\sqrt{18}-\sqrt{6})=25(3\sqrt{2}-\sqrt{6})N\]
Resolution of a given force into two components at right angles to one another
In this case, the components are referred to as the resolved parts of the force in the corresponding directions.
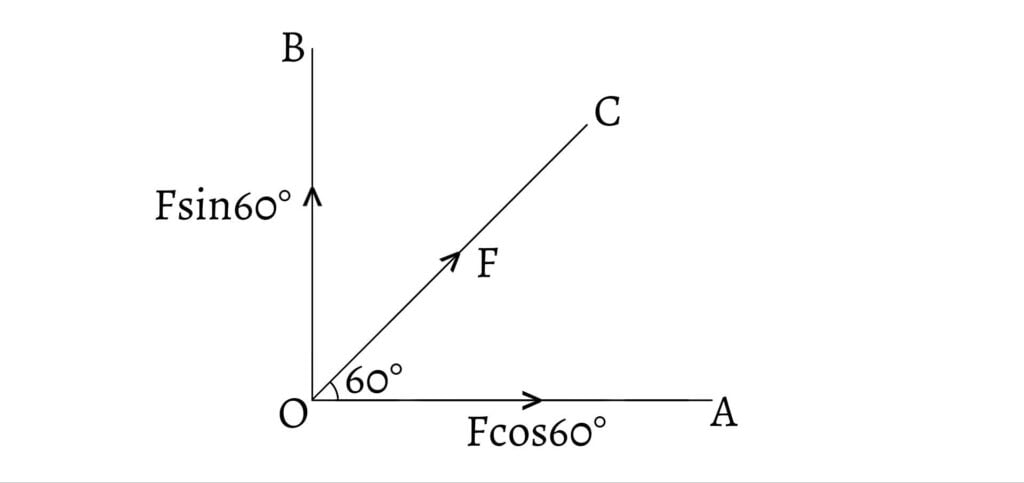
Let $OC$ represents the given force $F$ which has to be resolved along two perpendicular directions $OX$ and $OY$.

From $C$, draw $CA$ and $CB$ parallel to $YO$ and $XO$ respectively. Then, $OACB$ is a rectangle having $OC$ as its diagonal. Then, by parallelogram law of forces, $OA$ and $OB$ represent the two components of force $F$.
Since $AC$ and $OB$ are equal and parallel so they represent same force. If $\angle XOC=\theta$, then in figure $\text{(i)}$, in $\Delta OAC$, \[\sin\theta=\frac{AC}{OC}\] \[AC=OC\sin\theta\] \[\therefore OB=F\sin\theta\] \[\text{and, }\cos\theta=\frac{OA}{OC}\] \[\therefore OA=OC\cos\theta=F\cos\theta\]
In figure $\text{(ii)}$, in $\Delta OAC$, \[\sin(π-\theta)=\frac{AC}{OC}\] \[AC=OC\sin(π-\theta)\] \[\therefore OB=F\sin\theta\] \[\text{and, }\cos(π-\theta)=\frac{OA}{OC}\] \[OA=OC\cos(π-\theta)\] \[\therefore OA=-F\cos\theta\]
In figure $\text{(ii)}$, $OA=-F\cos\theta$ is positive along $OX’$. Mathematically, a force $F$ along $OX’$ is equal to a force $-F$ along $OX$. Thus, $-F\cos\theta$ along $OX’$ may be described as $F\cos\theta$ along $OX$.
Hence, any given force $F$ is equal to resolved parts;
- $F\cos\theta$, along a given direction $OX$ at an angle $\theta$ to it.
- $F\sin\theta$, which is perpendicular to $OX$.
whether, $\theta$ is acute or obtuse.
Therefore, a force equal to $10N$ making an angle $30°$ to the horizon is equivalent to;
- $10\cos30°=5\sqrt{3}N$ along horizontal direction
- $10\sin30°=5N$ along vertical direction
The algebraic sum of the resolved parts of any two given forces acting at a point and in the given directions, is equal to the resolved part of their resultant, in the same direction.
Let the two forces be $P$ and $Q$ acting at a point $O$ are represented by $OA$ and $OB$ respectively. Let their resultant be $R$ which is represented in magnitude and direction by $OC$, the diagonal of parallelogram $OACB$.

Let $OX$ be the given direction drawn through $O$. Let $AL$, $BM$ and $CN$ be the perpendiculars drawn in $OX$ from $A$, $B$ and $C$ respectively so that $OL$, $OM$ and $ON$ represent the resolved parts of $P$, $Q$ and $R$ along $OX$ in magnitude and sign. In figure $\text{(1)}$, $OM$, $OL$ and $ON$, all are positive. In figure $\text{(2)}$, $ON$ and $OL$ are positive but $OM$ is negative.
Since $OB$ and $AC$ are equal and positive, their projections $OM$ and $LN$ on $OX$ are equal in magnitude. \[OM=LN\]
In figure $\text{(1)}$, \[ON=OL+LN\] \[ON=OL+OM\]
In figure $\text{(2)}$, \[ON=OL-NL\] \[ON=OL-MO\] \[ON=OL-(-OM)\] \[ON=OL+OM\]
Thus, resolved parts of the resultant $R$ is equal to the algebraic sum of the resolved parts of $P$ and $Q$ along $OX$.
If the forces $P$ and $Q$ acting at $O$, and their resultant $R$, make angles $\alpha$, $\beta$ and $\theta$ respectively with $OX$, then, \[R\cos\theta=P\cos\alpha+Q\cos\beta\] \[R\sin\theta=P\sin\alpha+Q\sin\beta\]
This theorem may be extended to the resultant of any number of forces acting at a point as,
The algebraic sum of the resolved parts of any number of forces acting at a point and in the given directions, is equal to the resolved part of their resultant in the same direction.
If $P, Q, R, S, …$ are forces acting at $O$ and inclined at angles $\alpha,\beta,\gamma,\delta,…$ with positive $\text{X-axis}$ and $F$ is their resultant making an angle $\theta$ with the positive $\text{X-axis}$ then \[F\cos\theta=P\cos\alpha+Q\cos\beta+R\cos\gamma+S\cos\delta+…\] \[F\sin\theta=P\sin\alpha+Q\sin\beta+R\sin\gamma+S\sin\delta+…\]
See also: Composition of Forces
