Vector Product of Two Vectors

When two vectors are multiplied in such a way that their product is a vector quantity then it is called vector product or cross product of two vectors.

Let $\overrightarrow{a}=(a_1,a_2)$ and $\overrightarrow{b}=(b_1,b_2)$ be two vectors in the Cartesian plane (i.e. xy plane) then the vector product of the two vectors $\overrightarrow{a}$ and $\overrightarrow{b}$, denoted by $\overrightarrow{a}×\overrightarrow{b}$ (read $\overrightarrow{a}$ cross $\overrightarrow{b}$) is defined by

\[\overrightarrow{a}×\overrightarrow{b}=(a_1b_2-a_2b_1)\:\overrightarrow{k}\] where $\overrightarrow{k}$ is the standard unit vector along the positive z-axis.

In other words, \[\overrightarrow{a}×\overrightarrow{b}=(a_1b_2-a_2b_1)\:\overrightarrow{k}\] \[=(a_1b_2-a_2b_1)(0,0,1)\] \[=(0,0,a_1b_2-a_2b_1)\]

Let $\overrightarrow{a}=(a_1,a_2,a_3)$ and $\overrightarrow{b}=(b_1,b_2,b_3)$ be two space vectors. Then, the vector product of $\overrightarrow{a}$ and $\overrightarrow{b}$ is defined by, \[\overrightarrow{a}×\overrightarrow{b}=(a_1,a_2,a_3)×(b_1,b_2,b_3)\] \[=(a_2b_3-a_3b_2, a_3b_1-a_1b_3, a_1b_2-a_2b_1)\]

This vector $\overrightarrow{a}×\overrightarrow{b}$ is perpendicular to the plane of the vectors $\overrightarrow{a}$ and $\overrightarrow{b}$. The components of the vector $\overrightarrow{a}×\overrightarrow{b}$ can be obtained by the following rule.

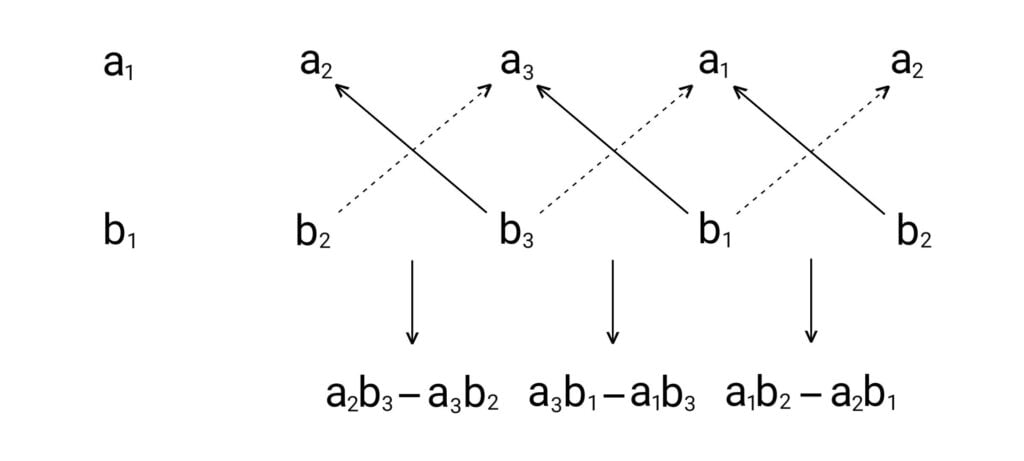
Alternative Definition of Vector Product

The vector product or cross product of two vectors $\overrightarrow{a}$ and $\overrightarrow{b}$ denoted by $\overrightarrow{a}×\overrightarrow{b}$ is a vector which is perpendicular to the plane of the vectors $\overrightarrow{a}$ and $\overrightarrow{b}$ and whose magnitude is equal to the product of the magnitudes of the two vectors and sine of the angle between them.

If $\theta$ is the angle between the two vectors $\overrightarrow{a}$ and $\overrightarrow{b}$, then \[\overrightarrow{a}×\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|\sin\theta\: \overrightarrow{n}\] where, $\overrightarrow{n}$ is the unit vector normal to $\overrightarrow{a}$ and $\overrightarrow{b}$.

The direction of $\overrightarrow{n}$ or $\hat{n}$ is perpendicular to the plane containing $\overrightarrow{a}$ and $\overrightarrow{b}$ and it points in the direction as given by right handed screw rule or right hand thumb rule.

If the cross product of one vector $(\overrightarrow{a})$ to another $(\overrightarrow{b})$ is made turning in anticlockwise, the direction of product i.e. of $\overrightarrow{n}$ will be upward and positive. But if the product be made turning in clockwise, the direction of product will be downward and negative.

Vector Product of Two Vectors in Determinant Form

Let two space vectors be \[\overrightarrow{a}=(a_1,a_2,a_3)=a_1\:\overrightarrow{i}+ a_2\:\overrightarrow{j}+ a_3\:\overrightarrow{k}\] \[\overrightarrow{b}=(b_1,b_2,b_3)=b_1\:\overrightarrow{i}+ b_2\:\overrightarrow{j}+ b_3\:\overrightarrow{k}\]

Then, \[\overrightarrow{a}×\overrightarrow{b}=(a_1,a_2,a_3)×(b_1,b_2,b_3)\] \[=(a_2b_3-a_3b_2, a_3b_1-a_1b_3, a_1b_2-a_2b_1)\] \[=(a_2b_3-a_3b_2)\:\overrightarrow{i}+(a_3b_1-a_1b_3)\:\overrightarrow{j}+ (a_1b_2-a_2b_1)\:\overrightarrow{k}\] \[=(a_2b_3-a_3b_2)\:\overrightarrow{i}-(a_1b_3-a_3b_1)\:\overrightarrow{j}+ (a_1b_2-a_2b_1)\:\overrightarrow{k}\] \[=\left|\begin{array}{c} \overrightarrow{i} & \overrightarrow{j} & \overrightarrow{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{array} \right|\]

Expression for $\sin\theta$

Let $\overrightarrow{a}=(a_1,a_2,a_3)$ and $\overrightarrow{b}=(b_1,b_2,b_3)$ be two space vectors. Let $\theta$ be the angle between them. Then,

\[\overrightarrow{a}×\overrightarrow{b}=(a_1,a_2,a_3)×(b_1,b_2,b_3)\] \[=(a_2b_3-a_3b_2, a_3b_1-a_1b_3, a_1b_2-a_2b_1)\] and, \[\overrightarrow{a}\cdot\overrightarrow{b}=a_1b_1+a_2b_2+a_3b_3=ab\cos \theta\]

Now, \[(\overrightarrow{a}×\overrightarrow{b})^2=(\overrightarrow{a}×\overrightarrow{b})\cdot (\overrightarrow{a}×\overrightarrow{b})\] \[=(a_2b_3-a_3b_2)^2+(a_3b_1-a_1b_3)^2+(a_1b_2-a_2b_1)^2\] \[=(a_1^2+a_2^2+a_3^2)(b_1^2+b_2^2+b_3^2)-(a_1b_1+a_2b_2+a_3b_3)^2\] \[=a^2b^2-(\overrightarrow{a}×\overrightarrow{b})^2\]

\[\text{or,}\;|\overrightarrow{a}×\overrightarrow{b}|^2=|\overrightarrow{a}|^2|\overrightarrow{b}|^2- |\overrightarrow{a}|^2|\overrightarrow{b}|^2\cos^2\theta\] \[=|\overrightarrow{a}|^2|\overrightarrow{b}|^2 (1-\cos^2\theta)\] \[=|\overrightarrow{a}|^2|\overrightarrow{b}|^2\sin^2\theta\]

\[\therefore|\overrightarrow{a}×\overrightarrow{b}|=|\overrightarrow{a}||\overrightarrow{b}|\sin\theta\] \[\therefore\sin\theta=\frac{|\overrightarrow{a}×\overrightarrow{b}|}{|\overrightarrow{a}| |\overrightarrow{b}|}\]

Geometrical Interpretation of Vector Product of Two Vectors

Let the two vectors $\overrightarrow{a}$ and $\overrightarrow{b}$ be represented by $\overrightarrow{OA}$ and $\overrightarrow{OB}$ respectively. Let $\theta$ be the angle between the vectors.

\[\therefore\overrightarrow{OA}=\overrightarrow{a}\;\;\text{and}\;\;\overrightarrow{OB}= \overrightarrow{b}\] Draw a parallelogram $OACB$. Join $AB$ and from $B$, draw $BN\perp OA$.

Now, the magnitude of $\overrightarrow{a}×\overrightarrow{b}$ is given by, \[|\overrightarrow{a}×\overrightarrow{b}|=ab\sin\theta\]

Again, area of the parallelogram $OACB$ \[=OA×BN\] \[=OA×OB\sin\theta\] \[=ab\sin\theta\]

Hence, the magnitude of cross product of two vectors $\overrightarrow{a}$ and $\overrightarrow{b}$ is equal to the area of the parallelogram with magnitudes of $\overrightarrow{a}$ and $\overrightarrow{b}$ as its adjacent sides.

Cor. Since the area of the parallelogram $OACB$ is twice the area of the triangle $OAB$, we have, \[|\overrightarrow{a}×\overrightarrow{b}|=2\Delta OAB\]

Hence, the magnitude of cross product of two vectors is equal to twice the area of a triangle whose sides are represented by $\overrightarrow{a}$ and $\overrightarrow{b}$.

Unit Vectors

The three mutually perpendicular unit vectors $\overrightarrow{i}$, $\overrightarrow{j}$ and $\overrightarrow{k}$ in space are defined by $(1,0,0)$, $(0,1,0)$ and $(0,0,1)$ respectively. Then,

\[\overrightarrow{i}×\overrightarrow{i}=(1,0,0)×(1,0,0)=(0,0,0)=0\] Similarly, \[\overrightarrow{j}×\overrightarrow{j}=\overrightarrow{k}×\overrightarrow{k}=0\]

Again, \[\overrightarrow{i}×\overrightarrow{j}=(1,0,0)×(0,1,0)=(0,0,1)=\overrightarrow{k}\] Similarly, \[\overrightarrow{j}×\overrightarrow{k}=\overrightarrow{i}\;\;\text{and}\;\;\overrightarrow{k}×\overrightarrow{i}=\overrightarrow{j}\]

Further, \[\overrightarrow{j}×\overrightarrow{i}=(0,1,0)×(1,0,0)=(0,0,-1)\]\[=-(0,0,1)=-\overrightarrow{k}\] Similarly, \[\overrightarrow{k}×\overrightarrow{j}=-\overrightarrow{i}\;\;\text{and}\;\;\overrightarrow{i}×\overrightarrow{k}=-\overrightarrow{j}\]

The value of the cross product of two mutually perpendicular unit vectors can be remembered by using the diagram circle.

Properties of Vector Product

1. The vector product of $\overrightarrow{a}×\overrightarrow{b}$ is perpendicular to both $\overrightarrow{a}$ and $\overrightarrow{b}$.

Let $\overrightarrow{a}=(a_1,a_2,a_3)$ and $\overrightarrow{b}=(b_1,b_2,b_3)$. Then, \[\overrightarrow{a}×\overrightarrow{b}=(a_2b_3-a_3b_2,a_3b_1-a_1b_3,a_1b_2-a_2b_1)\]

Now, \[(\overrightarrow{a}×\overrightarrow{b})\cdot\overrightarrow{a}\] \[=(a_2b_3-a_3b_2,a_3b_1-a_1b_3,a_1b_2-a_2b_1)\cdot(a_1,a_2,a_3)\] \[=(a_2b_3-a_3b_2)a_1+(a_3b_1-a_1b_3)a_2+(a_1b_2-a_2b_1)a_3\] \[=0\]

$\therefore$ $\overrightarrow{a}×\overrightarrow{b}$ is perpendicular to $\overrightarrow{a}$.

Similarly, $\overrightarrow{a}×\overrightarrow{b}$ is perpendicular to $\overrightarrow{b}$.

2. The vector product of two vectors is not commutative i.e. if $\overrightarrow{a}$ and $\overrightarrow{b}$ be two vectors then \[\overrightarrow{a}×\overrightarrow{b}≠\overrightarrow{b}×\overrightarrow{a}\]

Let $\overrightarrow{a}=(a_1,a_2,a_3)$ and $\overrightarrow{b}=(b_1,b_2,b_3)$.

Now, \[\overrightarrow{a}×\overrightarrow{b}=\left|\begin{array}{c} \overrightarrow{i} & \overrightarrow{j} & \overrightarrow{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{array} \right| \] \[=-\left|\begin{array}{c} \overrightarrow{i} & \overrightarrow{j} & \overrightarrow{k} \\ b_1 & b_2 & b_3 \\ a_1 & a_2 & a_3 \end{array} \right| \;\; (R_1\leftrightarrow R_2)\] \[=-\overrightarrow{b}×\overrightarrow{a}\]

\[\therefore\overrightarrow{a}×\overrightarrow{b}≠\overrightarrow{b}×\overrightarrow{a}\]

3. Distributive Law

If $\overrightarrow{a}$, $\overrightarrow{b}$, $\overrightarrow{c}$ be any three vectors, then \[\overrightarrow{a}×(\overrightarrow{b}+\overrightarrow{c})=\overrightarrow{a}×\overrightarrow{b}+\overrightarrow{a}×\overrightarrow{c}\]

Let $\overrightarrow{a}=(a_1,a_2,a_3)$, $\overrightarrow{b}=(b_1,b_2,b_3)$ and $\overrightarrow{c}=(c_1,c_2,c_3)$.

Then, \[\overrightarrow{b}+\overrightarrow{c}=(b_1,b_2,b_3)+(c_1,c_2,c_3)\] \[=(b_1+c_1,b_2+c_2,b_3+c_3)\]

Now, \[\overrightarrow{a}×(\overrightarrow{b}+\overrightarrow{c})=\left|\begin{array}{c} \overrightarrow{i} & \overrightarrow{j} & \overrightarrow{k} \\ a_1 & a_2 & a_3 \\ b_1+c_1 & b_2+c_2 & b_3+c_3 \end{array} \right|\]

\[=\left|\begin{array}{c} \overrightarrow{i} & \overrightarrow{j} & \overrightarrow{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{array} \right|+\left|\begin{array}{c} \overrightarrow{i} & \overrightarrow{j} & \overrightarrow{k} \\ a_1 & a_2 & a_3 \\ c_1 & c_2 & c_3 \end{array} \right|\]

[Each element of $R_3$ being the sum of two terms]

\[=\overrightarrow{a}×\overrightarrow{b}+\overrightarrow{a}×(\overrightarrow{c}\] \[\therefore\overrightarrow{a}×(\overrightarrow{b}+\overrightarrow{c})=\overrightarrow{a}×\overrightarrow{b}+\overrightarrow{a}×\overrightarrow{c}\]

4. For any scalar $n$, \[(n\:\overrightarrow{a})×\overrightarrow{b}=n(\overrightarrow{a}×\overrightarrow{b})=\overrightarrow{a}×(n\:\overrightarrow{b})\]

Let $\overrightarrow{a}=(a_1,a_2,a_3)$ and $\overrightarrow{b}=(b_1,b_2,b_3)$. Then, \[n\:\overrightarrow{a}=(na_1,na_2,na_3)\]

Now, \[(n\:\overrightarrow{a})×\overrightarrow{b}=\left|\begin{array}{c} \overrightarrow{i} & \overrightarrow{j} & \overrightarrow{k} \\ na_1 & na_2 & na_3 \\ b_1 & b_2 & b_3 \end{array} \right|\] \[=n \left|\begin{array}{c} \overrightarrow{i} & \overrightarrow{j} & \overrightarrow{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{array} \right|\] \[=n(\overrightarrow{a}×\overrightarrow{b})\]

Similarly, \[\overrightarrow{a}×(n\:\overrightarrow{b})=n(\overrightarrow{a}×\overrightarrow{b})\] \[\therefore(n\:\overrightarrow{a})×\overrightarrow{b}=n(\overrightarrow{a}×\overrightarrow{b})=\overrightarrow{a}×(n\:\overrightarrow{b})\]

Examples of Vector Product of Two Vectors

1. Torque $(\overrightarrow{\tau})$ acting on a particle is equal to the cross product of its position vector $(\overrightarrow{r})$ and force vector $(\overrightarrow{F})$ i.e. \[\overrightarrow{\tau}= \overrightarrow{r}×\overrightarrow{F}\]
2. Angular momentum $(\overrightarrow{L})$ of a particle is equal to the cross product of its position vector $(\overrightarrow{r})$ and its linear momentum $(\overrightarrow{P})$ i.e. \[\overrightarrow{L}=\overrightarrow{r}×\overrightarrow{P}\]
3. Linear velocity $(\overrightarrow{v})$ of a particle in rotational motion is equal to the cross product of its angular velocity $(\overrightarrow{\omega})$ and its displacement vector $(\overrightarrow{r})$ i.e. \[\overrightarrow{v}=\overrightarrow{\omega}×\overrightarrow{r}\]
4. Tangential acceleration $(\overrightarrow{a})$ of a particle in rotational motion is equal to the cross product of its angular acceleration $(\overrightarrow{\alpha})$ and its position vector $(\overrightarrow{r})$ i.e. \[\overrightarrow{a}=\overrightarrow{\alpha}×\overrightarrow{r}\]