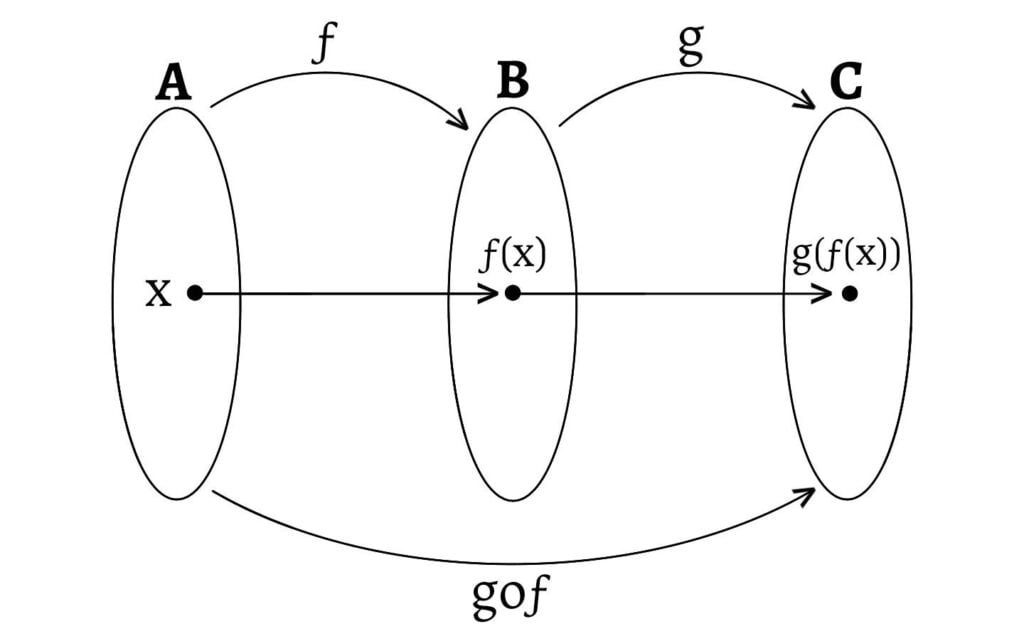
Let $ƒ: A\to B$ and $g: B\to C$ be any two functions. Suppose $x∈A$, then its image $ƒ(x)∈B$. $B$ being the domain of $g$, we can find the image of $ƒ(x)∈B$ under $g$, i.e., $g(ƒ(x))∈C$. In other words, we can associate an element $x∈A$ with a unique element $g(ƒ(x))∈C$. Hence, we have a function from $A$ to $C$. This is known as composition of functions and the new function is known as the composite function of $ƒ$ and $g$ (not $g$ and $ƒ$). It is denoted by $goƒ$ or $g(ƒ)$.
If $ƒ: A\to B$ and $g: B\to C$ be any two functions, then the composite function of $ƒ$ and $g$ is the function $goƒ: A\to C$ and defined by the equation, \[(goƒ)(x)=g(ƒ(x))\] Composite function is also known as product function or function of a function.
Examples:
- Let $A$, $B$ and $C$ denote the sets of real numbers. Suppose $ƒ: A\to B$ and $g: B\to C$ are defined by \[ƒ(x)=x-1\] \[g(x)=x^2\] Then, \[(goƒ)(x)=g(ƒ(x))\] \[=g(x-1)\] \[=(x-1)^2\]
- Suppose $ƒ: A\to B$ and $g: B\to C$ are defined by the following diagram:
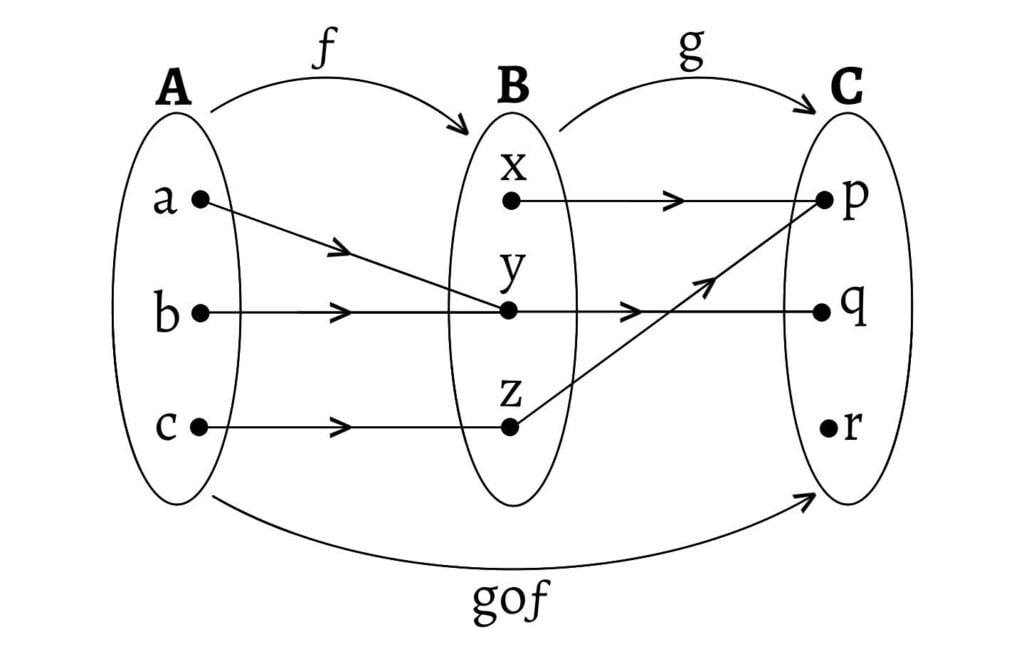
Here, \[(goƒ)(a)=g(ƒ(a))=g(y)=q\] \[(goƒ)(b)=g(ƒ(b))=g(y)=q\] \[(goƒ)(c)=g(ƒ(c))=g(z)=p\]
Properties of Composite Functions
- If $ƒ: A\to B$, $g: B\to C$ and $h: C\to D$, then \[(ho(goƒ))(x)=h((goƒ)(x))=h(g(ƒ(x)))\] \[((hog)oƒ)(x)=(hog)(ƒ(x))=h(g(ƒ(x)))\] \[\text{for any x∈A.}\] \[\therefore ho(goƒ)=(hog)oƒ\] Hence, composite function satisfies associative property.
- If $ƒ: A\to B$ and $g: B\to C$ are given functions, then $goƒ$ is onto or one-one according as each of $ƒ$ and $g$ is onto or one-one.
If $ƒ$ is onto, $ƒ(A)=B$, and so for any $x∈A$, $ƒ(x)∈B$. Since $g$ is onto, $g(B)=C$ for any $ƒ(x)∈B$, $g(ƒ(x))∈C$. But \[g(ƒ(x))=(goƒ)(x)\] \[\therefore (goƒ)(A)=C\] Hence, $goƒ$ is onto.
If $ƒ$ is one-one, every element of $A$ has a distinct image in $B$. And, since $g$ is one-one, every element of $B$ has a distinct image in $C$. So, for any $x∈A$, $goƒ(x)$ is unique. Hence, $goƒ$ is one-one.
More on Relations And Functions
