Biot-Savart Law is used to determine the magnetic field due to current. Some of its applications are as follows:
- Magnetic field at a point due to a straight current carrying conductor
- Magnetic field at the centre of current carrying circular coil
- Magnetic field at a point on the axis of a current carrying circular coil
- Magnetic field at a point on the axis of a solenoid
Magnetic field at a point due to a straight current carrying conductor
Let $AC$ be a long straight conductor having current $I$ in upward direction. Let $P$ be the point at distance $a$ from the conductor where magnetic field is to be calculated such that $OP=a$. A small element of length $dl$ of the conductor is taken at a distance $r$ from the point $P$.
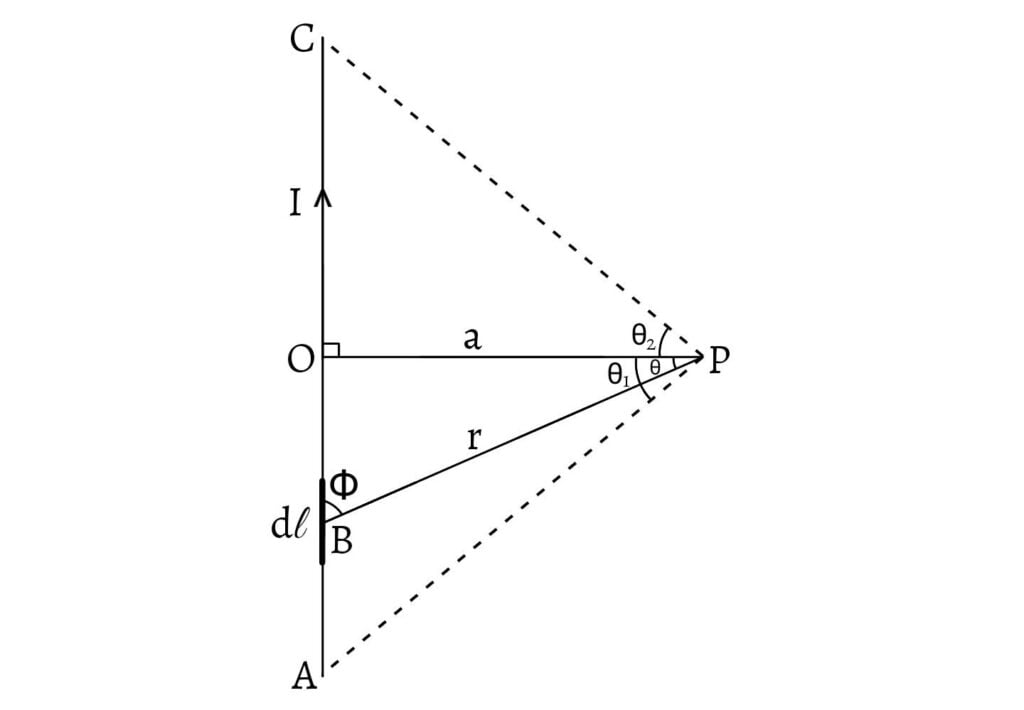
According to Biot-Savart Law, the magnetic field at the point $P$ due to current element $dl$ is given by, \[dB=\frac{\mu_o}{4π}\frac{Idl\sin\phi}{r^2} \text{ __(a)}\]
In rt. angled $∆POB$, \[\sin\phi=\frac{a}{r}=\cos\theta\] \[\text{or, } r=\frac{a}{\cos\theta}\] Also, \[\tan\theta=\frac{l}{a}\] \[\text{or, } l=a\tan\theta\]
Differentiating both sides with respect to $\theta$, \[\frac{dl}{d\theta}=\frac{d}{d\theta}(a\tan\theta)=a\sec^2\theta\] \[\therefore dl=a\sec^2\theta d\theta\]
Putting the values of $r$ and $dl$ in equation $\text{(a)}$, we get, \[dB=\frac{\mu_o}{4π}\frac{I(a\sec^2\theta d\theta)}{\left(\frac{a^2}{\cos^2\theta}\right)}(\cos\theta)\] \[dB=\frac{\mu_o}{4π} \frac{Ia\sec^2\theta d\theta}{a^2}\cos^2\theta \cos\theta\] \[dB=\frac{\mu_o}{4π}\frac{I\cos\theta d\theta}{a} \text{ __(b)}\]
Magnetic field due to whole conductor $AC$ can be calculated by integrating equation $\text{(b)}$ with limits $\theta_2$ and $-\theta_1$. By convention, $\theta_1$ being anticlockwise is taken as negative. \[B=\frac{\mu_oI}{4πa} \int_{-\theta_1}^{\theta_2} \cos\theta d\theta\] \[B=\frac{\mu_oI}{4πa}[\sin\theta]_{-\theta_1}^{\theta_2}\] \[B=\frac{\mu_oI}{4πa} [\sin\theta_2+\sin\theta_1]\] \[B=\frac{\mu_oI}{4πa}(\sin\theta_1+\sin\theta_2)\]
This equation gives the value of $B$ at point $P$ due to a straight conductor of finite length. For an infinitely long conductor, $\theta_1=\theta_2=\frac{π}{2}$. \[B=\frac{\mu_o}{4πa}\left(\sin\frac{π}{2}+\sin\frac{π}{2}\right)\] \[B=\frac{\mu_oI}{4πa}×2\] \[\therefore B=\frac{\mu_oI}{2πa}\]
The straight conductor of infinite length means that the point $P$ is so close that its distance may be negligible in comparison to the length of the conductor. The direction of $B$ can be found by using right hand thumb rule which is directed inward to the plane of screen at $P$.
This relation is only applicable for a thin wire. For a thick wire, the magnetic field $(B)$ decreases as distance from the surface of the wire increases either inside or outside the surface according to the following graph:

Here, $R$ is the radius of the wire and $r$ is the distance of the observed point from the centre of wire. Hence, the magnetic field is maximum on the surface of the wire $(r=R)$.
Magnetic field at the centre of current carrying circular coil
Consider a circular coil of radius $r$ carrying current $I$. Let $PQ=dl$ be the current element and $R$ be its midpoint such that $OR=r$.

The angle between current element $PQ$ and $OR$ is $90°$. According to Biot-Savart Law, the magnetic field at the centre due to the current element $PQ$ is, \[dB=\frac{\mu_o}{4π} \frac{Idl\sin90°}{r^2}\] \[dB=\frac{\mu_o}{4π}\frac{Idl}{r^2}\]
By integrating this equation from $0$ to the circumference of the coil $2πr$, we can find the magnetic field due to the whole coil, \[B=\int_0^{2πr} \frac{\mu_o}{4π}\frac{Idl}{r^2}\] \[B=\frac{\mu_oI}{4πr^2}\int_0^{2πr} dl\] \[=\frac{\mu_oI}{4πr^2}[l]_0^{2πr}=\frac{\mu_oI}{4πr^2}(2πr)\]\[\therefore B=\frac{\mu_oI}{2r}\]
For the coil having $N$ turns, \[B=\frac{\mu_oNI}{2r}\]
Its direction can be found out by right hand thumb rule. It is perpendicular to the plane of this screen and is directed outward.
Magnetic field at a point on the axis of a current carrying circular coil
Consider a circular coil of radius $a$ centred at $O$ carrying a current $I$. Let $P$ be a point on the axis of the coil at a distance $x$ from the centre $O$. Let $XY$ be a current element of length $dl$ whose midpoint be $M$ which is joined to the point $P$ such that $MP=r$.
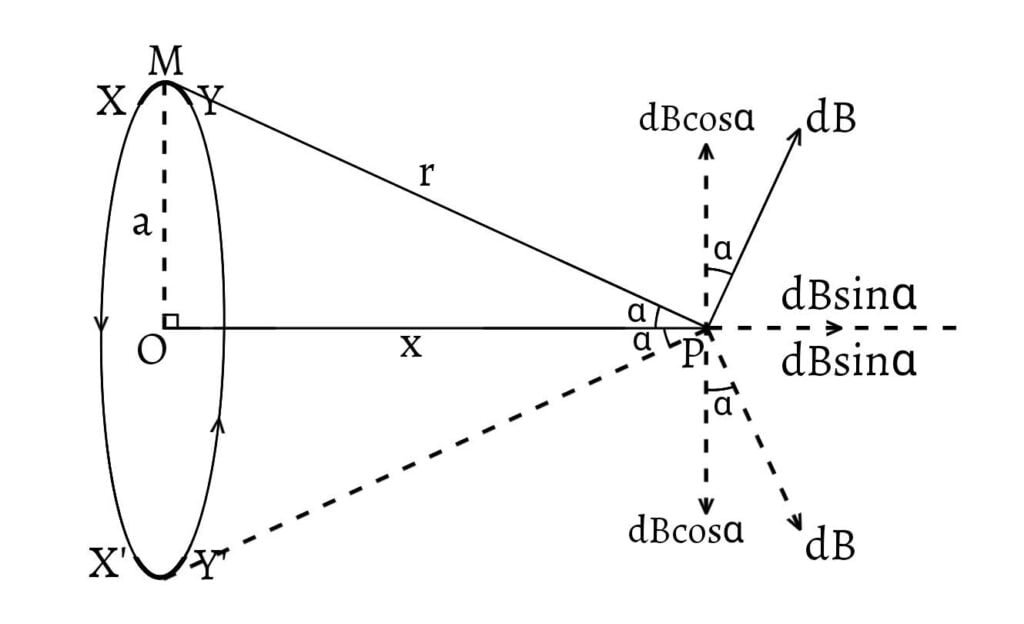
Because of small value of $dl$, angle between $XY$ and $MP$ is $90°$. Then, according to Biot-Savart law, the magnetic field at the point $P$ due to the current element $XY$ is,
\[dB=\frac{\mu_o}{4π}\frac{Idl\sin90°}{r^2}\] \[dB=\frac{\mu_o}{4π}\frac{Idl}{r^2}\]
The direction of $dB$ at $P$ is along $PA$ i.e. perpendicular to the plane formed by $dl$ and $r$. Let $\alpha$ be the angle between between $MP$ and the axis $OP$ of the loop. Then, $dB$ will have two components; $dB\cos\alpha$ along vertical direction and $dB\sin\alpha$ along horizontal direction.
As the coil is symmetrical about its axis, every element of length $dl$ has equal and opposite element at the end of a diameter of the coil. For example, $XY$ has an equal and opposite element $X’Y’$ which produces a magnetic field of equal strength but in other direction.
The vertical components are equal in magnitude but opposite in direction so they cancel each other. The horizontal components will add up giving the resultant field $B$ given by,
\[B=\int_0^{2πa} dB\sin\alpha=\int_0^{2πa} \frac{\mu_o}{4π} \frac{Idl}{r^2} \sin\alpha\] \[=\frac{\mu_o}{4π} \frac{I\sin\alpha}{r^2} \int_0^{2πa} dl\]\[=\frac{\mu_o}{4π} \frac{I\sin\alpha}{r^2} [dl]_0^{2πa}\] \[=\frac{\mu_o}{4π} \frac{I\sin\alpha}{r^2}(2πa)\] \[B=\frac{\mu_oI}{2r^2}a\sin\alpha\text{ ___(1)}\]
In $∆OPM$, $\sin\alpha=\frac{a}{r}$ and $r=(a^2+x^2)^{\frac{1}{2}}$. Now, \[B=\frac{\mu_oI}{2r^2}a.\frac{a}{r}\] \[B=\frac{\mu_oIa^2}{2r^3}\] \[\therefore B=\frac{\mu_oIa^2}{2(a^2+x^2)^{\frac{3}{2}}}\]
If the coil has $N$ turns, then, \[B=\frac{\mu_oNIa^2}{2(a^2+x^2)^{\frac{3}{2}}}\]
The direction of $B$ is along the axis of the coil towards or away according to the anticlockwise or clockwise direction of the current in the loop which can be figured out by right hand thumb rule.
Cases
- At the centre of the coil, $x=0$. \[\therefore B=\frac{\mu_oNIa^2}{2(a^2+0)^{\frac{3}{2}}}\] \[B=\frac{\mu_oNI}{2a} \text{ (Maximum Value)}\]
- When the point is far away from the centre of coil, then $x>>a$ so that $a_2+x_2≈x_2$. \[\therefore B=\frac{\mu_oNIa^2}{2(x^2)^{\frac{3}{2}}}\] \[B=\frac{\mu_oNIa^2}{2x^3}\]
Magnetic field at a point on the axis of a solenoid
Consider a long solenoid of radius $a$ having $n$ number of turns per unit length and carrying current $I$. To find out the magnetic field at a point $P$ on the axis of the solenoid, let us consider an element $MN$ of length $dx$ that makes an angle $d\beta$ at $P$. A perpendicular line $NT$ is drawn to radius vector $r$.
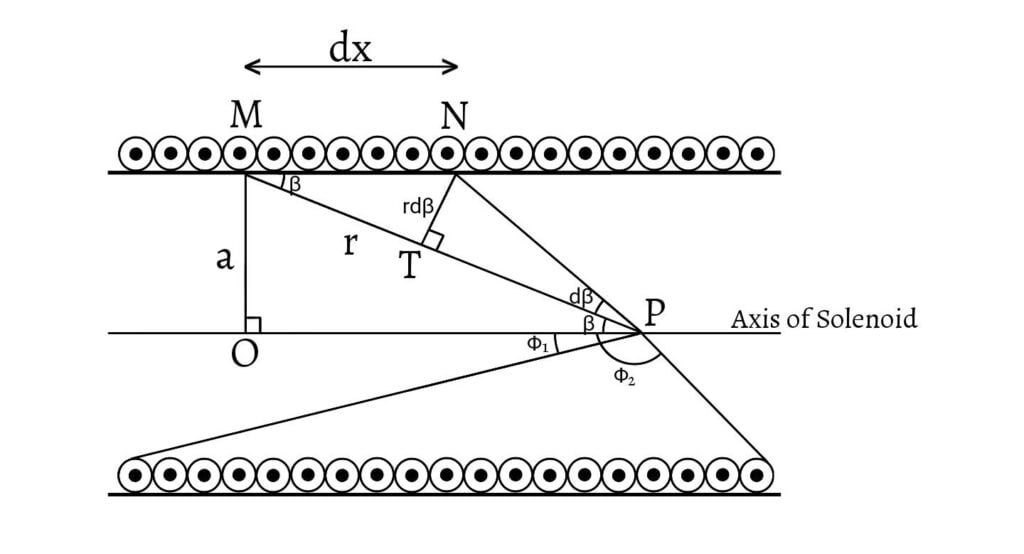
According to Biot-Savart law, the magnetic field at a point on the axis of a narrow circular coil is given by, \[dB=\frac{\mu_oNIa\sin\beta}{2r^2} \text{ [From (1)]}\]
Since unit metre gives $n$ turns, $dx$ metre gives $ndx$ turns. \[\therefore N=ndx\]
Thus, the field at point $P$ due to $dx$ part of the coil is given by, \[dB=\frac{\mu_oIa\sin\beta}{2r^2}ndx\text{ __(i)}\]
In $∆NTP$, for small angle $d\beta$, \[NT=rd\beta\text{ __(ii)}\]
In $∆MNT$, \[\sin\beta=\frac{NT}{MN}\] \[NT=MN\sin\beta=dx\sin\beta\text{ __(iii)}\]
From $\text{(ii)}$ and $\text{(iii)}$, \[rd\beta=dx\sin\beta\] \[dx=\frac{rd\beta}{\sin\beta}\]
Putting the value of $dx$ in equation $\text{(i)}$, \[dB=\frac{\mu_oIa\sin\beta}{2r^2}n\left(\frac{rd\beta}{\sin\beta}\right)\] \[dB=\frac{\mu_onIa}{2r}d\beta\]
In ∆MOP, \[\sin\beta=\frac{a}{r}\] \[\therefore d\beta=\frac{\mu_onI}{2}\sin\beta d\beta\]
If the radius vector $r$ makes angle $\phi_1$ and $\phi_2$ at $P$ from two ends of coil, the total magnetic field at the point $P$ is given by \[B=\int_{\phi_1}^{\phi_2} \frac{\mu_onI}{2}\sin\beta d\beta\] \[=\frac{\mu_onnI}{2} \int_{\phi_1}^{\phi_2} \sin\beta d\beta \] \[=\frac{\mu_onI}{2} [-\cos\beta]_{\phi_1}^{\phi_2}\] \[=\frac{\mu_onI}{2}[\cos\phi_1-\cos\phi_2]\]
For a very long solenoid, $\phi_1=0°$ and $\phi_2=π$. \[\therefore B=\frac{\mu_onI}{2} [cos0-cosπ]\] \[=\frac{\mu_onI}{2}[1-(-1)]\] \[=\frac{\mu_onI}{2}×2\] \[\therefore B=\mu_onI\]
This relation shows that the magnitude of magnetic field within a solenoid does not depend on the diameter or length of the solenoid. The direction of $B$ is along the axis of $OP$ of the solenoid which can be determined by right hand thumb rule.
