When a body moves in a circular path then the body is said to be in circular motion. If the body moves with a constant speed in the circular path, then the body is said to be in uniform circular motion.
Angular Displacement
Angular displacement is the angle made by radius vector at the centre within fixed interval of time.
Suppose a particle is moving in a circular path of radius $r$ and centred at $O$. Let $A$ be its position at any instant $t$ and suppose it reaches to a point $B$ at $t+∆t$.
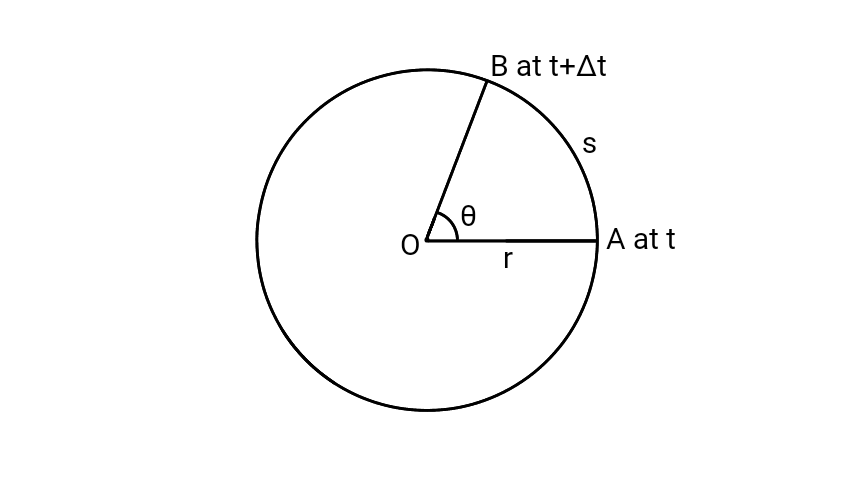
If $θ$ is the angle made by $OB$ with $OA$, then $θ$ is the angular displacement of the particle in time $∆t$. Then, angular displacement $θ$ is, \[θ=\frac{\text{Arc}}{\text{Radius}}\] \[θ=\frac{s}{r}\] where, arc $OA = s$ and radius $OA = r$.
The unit of angular displacement is radian. It is a dimensionless quantity [Dimensional Analysis].
Here, $π \text{ radian} = 180°$.
Angular Velocity
The rate of change of angular displacement with respect to time is known as angular velocity. It is denoted by $ω$.
Suppose the particle moving in a circular path is at position $B$ in time $t_1$ making angular displacement $theta_1$ and at position $C$ in time $t_2$ making angular displacement $θ_2$.

Then, angular velocity is given by, \[ω_{av}=\frac{\text{Change in angular displacement}}{\text{Time taken}}\] \[ω_{av}=\frac{θ_2-θ_1}{t_2-t_1}\] \[ω_{av}=\frac{Δθ}{Δt}\] The time rate of angular displacement when time interval approaches zero is known as instantaneous angular displacement. Instantaneous angular velocity is given by, \[ω=\lim_{Δt \to 0}\frac{Δθ}{Δt}\] \[ω=\frac{dθ}{dt}\] Its unit is $\text{rad s}^{-1}$.
Since its dimensional formula is $[M^0L^0T^{-1}]$, it is also known as angular frequency.
Time Period
Time period is the time taken by the particle to complete one revolution. It is denoted by $T$.
In time $T$, the particle completes one revolution that is of angular displacement $2π$ $\text{rad}$. Thus, angular velocity $ω$ is, \[ω=\frac{2π}{T}\]
Frequency
Frequency is the number of revolutions completed by the particle in one second. \[\text{Since, } f=\frac{1}{T}\] \[∴ω=2πf\]
Angular Acceleration
The rate of change of angular velocity with respect to time is called angular acceleration. It is denoted by $α$.
If the particle has angular velocity $ω_1$ at time $t_1$ and angular velocity $ω_2$ at time $t_2$, then, Average angular acceleration is given by, \[α_{av}=\frac{\text{Change in Angular Velocity}}{\text{Time taken}}\] \[α_{av}=\frac{ω_2-ω_1}{t_2-t_1}\] \[α_{av}=\frac{Δω}{Δt}\] The limiting value of average angular acceleration when time interval approaches zero is called instantaneous angular acceleration. Instantaneous angular acceleration is given by, \[α=\lim_{Δt\to 0}\frac{Δω}{Δt}\] \[α=\frac{dω}{dt}\] \[α=\frac{d}{dt}\left(\frac{dθ}{dt}\right)\] \[α=\frac{d²θ}{dt²}\] The unit of angular acceleration is $\text{rad s}^{-2}$.
Relation Between Linear Velocity And Angular Velocity
Here, Angular displacement $θ$ is, \[θ=\frac{Arc}{Radius}\] \[θ=\frac{s}{r}\] \[s=rθ\] Differentiating with respect to time $t$, \[\frac{ds}{dt}=r\frac{dθ}{dt}\text{ __(1)}\] Here, \[\frac{ds}{dt}=v\] $v$ is instantaneous linear velocity of the particle. At any point of the circular path, it acts along the tangent to the path of that point. and, \[\frac{dθ}{dt}=ω\] $ω$ is instantaneous angular velocity of the particle. Thus, from $\text{(1)}$, \[v=rω\]
Relation Between Linear Acceleration And Angular Acceleration
we have, \[v=rω\] Differentiating with respect to time $t$, \[\frac{dv}{dt}=r\frac{dω}{dt}\] \[a=rα\] where, $a$ is the linear acceleration, $r$ is the radius and $α$ is the angular acceleration of the particle.
More on Circular Motion
