Bernoulli’s theorem states that:
For the steady flow of a incompressible non-viscous fluid, the sum of pressure energy per unit mass, potential energy per unit mass and kinetic energy per unit mass remains constant at every point throughout the flow.
\[\text{i.e. } \frac{P}{ρ} + gh +\frac{v^2}{2} = constant\] where, \[\frac{P}{ρ}=\text{Pressure energy per unit mass}\] \[gh=\text{Potential energy per unit mass}\] \[\frac{v^2}{2}=\text{Kinetic energy per unit mass}\]
This theorem is an outcome of the principle of conservation of energy. Consider an incompressible non-viscous liquid is flowing inside a tube $XY$ of varying cross sectional area.
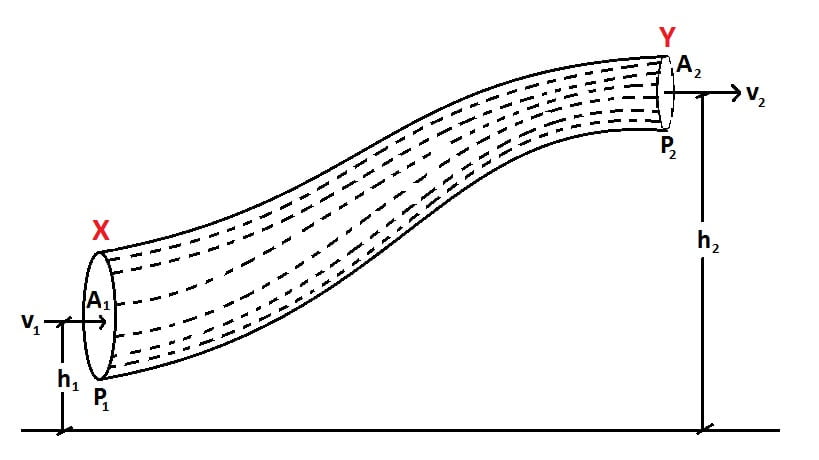
If the flow is steady, then the mass $m$ of the liquid flowing per second through any section of the tube is same. Let the density of the liquid be $ρ$.
Let, \[P_1=\text{Pressue at X}\] \[P_2=\text{Pressue at Y}\]
\[A_1=\text{Area of cross section of the tube at X}\] \[A_2=\text{Area of cross section of the tube at Y}\]
\[v_1=\text{Velocity of liquid at X}\] \[v_2=\text{Velocity of liquid at Y}\]
\[h_1=\text{Height of section X from ground}\] \[h_2=\text{Height of section Y from ground}\]
The flow work associated with the liquid at $X$, \[W_1=P_1A_1v_1\] where, $v_1$ is the distance travelled per second and \[F_1=P_1A_1\] \[∴W_1=P_1V\] where, $V$ is volume of liquid flowing per second.
Similarly, The flow work associated with the liquid at $Y$, \[W_2=P_2A_2v_2\] \[∴W_2=P_2V\]
Now, \[\text{Total work done (W)}=\text{Sum of two flow works}\] \[W=W_1+(-W_2)\] \[W=W_1-W_2\]
There is negative sign because the flow work at $Y$ is negative. \[∴W=P_1V-P_2V\] \[W=(P_1-P_2)V\] \[W=(P_1-P_2)\frac{m}{ρ}\text{ ____(1) }\left[ρ=\frac{m}{V}\right]\]
Potential energy increases from $X$ to $Y$ because the height is increasing. \[\text{Change in P.E. } ΔP.E.=mg(h_2-h_1)\]
Kinetic energy also increases from $X$ to $Y$ because the velocity increasing. \[\text{Change in K.E. } ΔK.E.=\frac{1}{2}m(v_2^2-v_1^2)\]
Now- \[\text{Total work done (W)}=ΔP.E+ΔK.E.\] \[W=mg(h_2-h_1)+\frac{1}{2}m(v_2^2-v_1^2)\text{ ____(2)}\]
From (1) and (2), \[(P_1-P_2)\frac{m}{ρ}=mg(h_2-h_1)+\frac{1}{2}m(v_2^2-v_1^2)\] \[\frac{P_1}{ρ}-\frac{P_2}{ρ}=gh_2-gh_1+\frac{v_2^2}{2}-\frac{v_1^2}{2}\] \[\frac{P_1}{ρ}+gh_1+\frac{v_1^2}{2}=\frac{P_2}{ρ}+gh_2+\frac{v_2^2}{2}\]
Hence, \[\frac{P}{ρ}+gh+\frac{v^2}{2}=constant\text{ ___(a)}\]
This verifies Bernoulli’s theorem. Also, multiplying $(a)$ by $ρ$, we get, \[P+ρ gh+\frac{ρv_1^2}{2}=constant\]
Thus, the sum of pressure energy per unit volume, potential energy per unit volume and kinetic energy per unit volume remains constant.
More on Fluid Dynamics
