Terminal velocity is the maximum constant velocity acquired by the body while falling freely in a viscous medium.
When a small spherical body falls through a viscous medium, then,
1. weight of the body acts vertically downwards
2. upthrust acts vertically upwards
3. viscous force acts opposite to the motion of the body i.e. upward.
When the body falls, it accelerates due to gravity. Hence, viscous force also goes on increasing with increase in velocity. After some time, the weight of the body becomes just equal to the sum of the upthrust and the viscous force. At this condition, there is no net force to accelerate the body. Hence, the body starts to move with a constant velocity called terminal velocity.
Thus, terminal velocity is the maximum constant velocity acquired by the body while falling freely in a viscous medium when its weight becomes just equal to the sum of the upthrust and the viscous force.
Let a spherical body of radius $r$ and density $ρ$ be falling in a viscous medium of density $σ$ and coefficient of viscosity $η$.
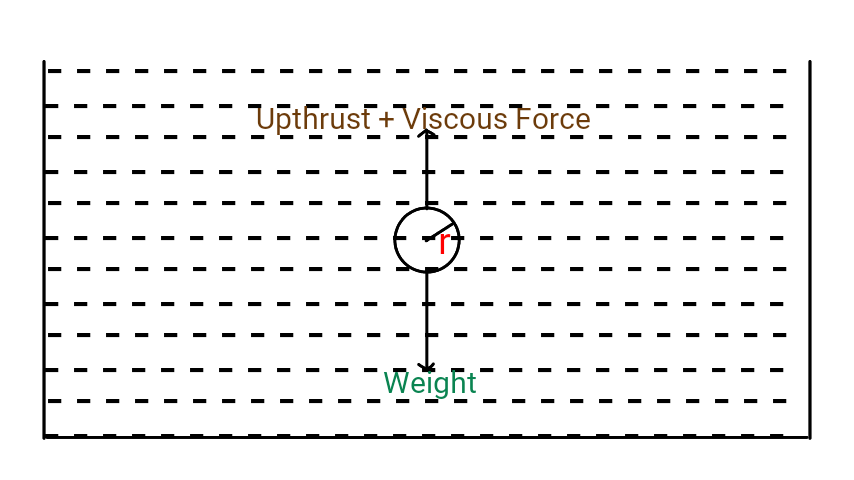
\[\text{Weight of the body} = \frac{4}{3} π r^3 ρ g\] \[{Upthrust} = \frac{4}{3} π r^3 σg\] And, according to Stoke’s law, \[{Viscous force} = 6 πηr v\] where, $v =$ terminal velocity acquired by the body When the body attains terminal velocity, then, \[\text{Weight}=\text{Upthrust}+\text{Viscous force}\] \[\frac{4}{3} π r^3 ρg=\frac{4}{3}π r^3σg+6 πη r v\] \[6 πη r v=\frac{4}{3} π r^3 (ρ-σ) g\] \[∴v=\frac{2r^2(ρ-σ)g}{9η}\]
If $ρ<σ$, then, $v$ is negative i.e. the body will go upward. That’s why, bubble rises in a liquid. \[∴η=\frac{2r^2(ρ-σ)g}{9v}\] This formula can be used to determine the coefficient of viscosity of the viscous medium.
More on Fluid Dynamics
