Every object with mass in this universe attracts each other. The force of attraction between any two bodies in the universe is called gravitational force. The sun attracts the earth and the earth also attracts the sun. The earth attracts moon and the moon also attracts the earth. Similarly, The earth attracts an apple on a tree and the apple also attracts the earth.
The effect of gravitational force can only be observed in a body with big mass. That’s why, all the planets revolve around the sun as the sun is so large in size and it has a large mass than any planets or satellites of our solar system.
Newton’s Universal Law of Gravitation
The universal law of gravitation was formulated by Newton in 1687 AD.
Newton’s universal law of gravitation states that
“an object in the universe attracts every other object with a force called gravitation which is directly proportional to the product of their masses and inversely proportional to the square of the distance between their centers.”
Calculation of Gravitational Force
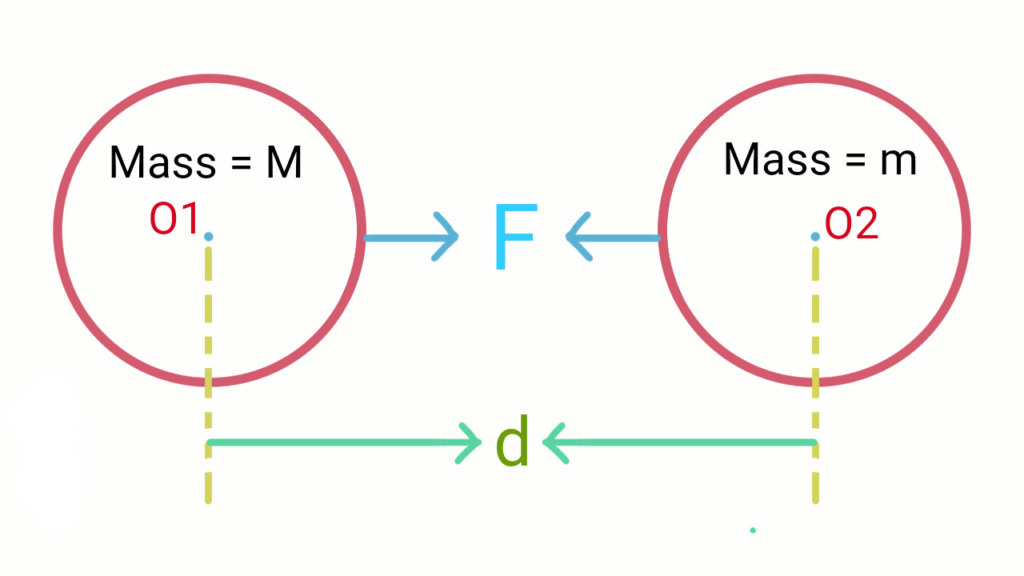
Let an object of mass $M$ attracts another object of mass $m$ towards its centre $O1$ with a force of $F$. Then the body of mass $m$ also attracts the body of mass $M$ towards its centre $O2$ with the same force $F$. Let the distance between their centres be $d$.
Then, according to the Newton’s universal law of gravitation,
\[F ∝ M × m\] \[F ∝ \frac{1}{d^2}\] From equations $(1)$ and $(2)$, \[F ∝ \frac{Mm}{d^2}\] \[F=\frac{GMm}{d^2}\] Where, $G$ is the Universal Gravitational Constant.
Universal Gravitational Constant (G)
The value of $G$ is constant everywhere in the universe. So, it is called as universal gravitational constant. It was calculated in the Cavendish Experiment which was performed in 1797 – 1798 AD by British scientist Henry Cavendish.
\[\text{We know, } F = \frac{GMm}{d^2}\]
Suppose an object of mass $1\text{ kg}$ attracts another object of mass $1\text{ kg}$ and the distance between their centres is $1\text{ m}$.
\[\text{Then, } F = G\]
Therefore, Universal Gravitational Constant $G$ can be defined as the gravitational force between two objects of mass $1\text{ kg}$ each, which are separated by the distance of $1\text{ m}$ from their centers.
The SI unit of $G$ is $\text{Nm}^2\text{/kg}^2$.
And, the approximate value of $G$ is $6.67×10^{-11}$ $\text{Nm}^2\text{/kg}^2$.
But why this force of attraction cannot be observed in small bodies?
It is because of the very small value of $G$. It is also known as the weakest force in nature. Due to this small value, the gravitational force between two bodies with small masses can’t be observed.
Let’s take an example; let two objects of each mass $50 \text{ kg}$ are separated by the distance of $1\text{ m}$ from their centres. \[\text{Then, }F = \frac{GMm}{d^2} \] \[ = \frac{6.67×10^{-11}×50×50}{1^2} = 1.6675×10^{-7} N\] Here, the value of gravitational force is too small. So, it can’t be noticed on small objects of earth.
But in the context of earth and sun, they have very big masses and the distance between them is about $1.5×10^7\text{ km}$. So, the gravitational force between them is $10^{27}\text{ N}$. This value is so big. So, this force of attraction can be easily noticed in them.

Tides occur in seas and oceans because of the gravational force of sun and moon as they both attracts the water of seas and oceans towards them. Here, the role of moon is more than the sun to cause tides because the distance between the moon and the earth is less than the distance between the sun and earth.

The earth keeps us on its surface due to its gravitational force.
Without Gravitational force, many things were not possible. Revolution of planets around the sun is caused by gravitational force.
Presence of atmosphere on earth is because of this force as the earth attracts the atmosphere towards its centre. Without this force, earth cannot hold the atmosphere and the atmosphere will escape out in space. So, without this force, even life on earth is not possible.