A motion that repeats itself after a regular interval of time is called harmonic motion.
For example, backward and forward motion of a simple pendulum, up and down motion of a mass attached to a spring [Helical Spring], etc. In harmonic motion, there is always an equilibrium position at which the body comes to rest. If the body is displaced from the equilibrium position, the system develops a restoring force in such a direction that brings it back to the equilibrium position.
In simple harmonic motion,
Restoring force $∝$ displacement from equilibrium position \[\text{i.e. }F ∝y\] \[F = ky\text{ ___(1)}\] From Newton’s Second Law of Motion, \[F=-ma \text{ ___(2)}\] There is negative sign because it is restoring force. from (1) and (2), \[ky=-ma\] \[a=-\frac{k}{m}y\] \[a ∝y\]
Thus, a body is said to be executing simple harmonic motion if its acceleration is directly proportional to the displacement from the mean position and is directed towards the mean position.
Uniform Circle as a Projection of SHM
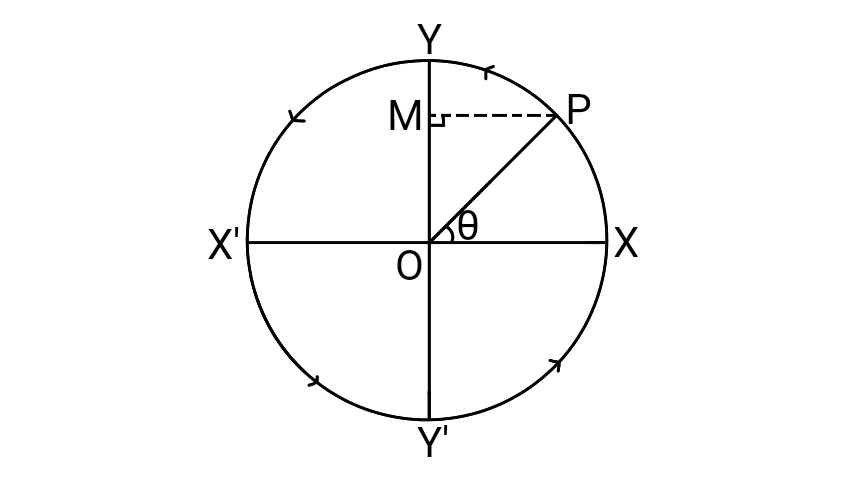
Consider a particle $P$ is moving in a circular path with uniform angular speed. At any instant, draw $PM⊥YY’$. The foot $M$ of the perpendicular is known as projection. When $P$ moves from $X$ to $Y$, its projection $M$ moves from $O$ to $Y$. And, when $P$ moves from $Y$ to $X’$, its projection $M$ moves from $Y$ to $O$. Similarly, when $P$ moves from $X’$ to $Y’$ and $Y’$ to $X$, its projection $M$ moves from $O$ to $Y’$ and $Y’$ to $O$ respectively. This back and forth motion of the projection $M$ along the diameter is simple harmonic motion.
Calculation of SHM
Displacement

Consider a circular path of radius $r$. Let an object initially at point $A$ reaches a point $B$ after some time $t$ with angular velocity $ω$. \[∴∠AOB=θ=ωt\] In triangle $OBM$, \[\sin θ=\frac{OM}{OB}\] \[\sin θ=\frac{y}{r}\] \[∴y=r\sin ωt\] This is the displacement $(y)$ of the object executing S.H.M. It is the displacement of the particle from the mean position at that time.
Velocity
\[\text{Velocity (v)} = \text{Rate of change of y}\] \[v=\frac{dy}{dt}\] \[v=\frac{d(r\sin ωt)}{dt}\] \[v=r\frac{d(\sin ωt)}{dωt} × \frac{d(ωt)}{dt}\] \[v=r \cos ωt × ω\] \[v=ω\sqrt{r^2\cos^2ωt}\] \[v=ω\sqrt{r^2(1-\sin^2ωt)}\] \[v=ω\sqrt{r^2-r^2\sin^2ωt}\] \[v=ω\sqrt{r^2-y^2}\] When the particle is at the extreme position i.e. $y=r$, then, \[v=ω\sqrt{r^2-r^2}=0\] ∴ Velocity is zero at the extreme position. When the particle is at the equilibrium position i.e. $y=0$, then, \[v=ω\sqrt{r^2-0}=rω\] ∴ Velocity is maximum at the equilibrium position.
Acceleration
\[Acceleration=\text{Rate of change of velocity}\] \[a=\frac{dv}{dt}\] \[a=\frac{d(rω\cos ωt)}{dt}\] \[a=rω\frac{d(\cos ωt)}{dωt} × \frac{d(ωt)}{dt}\] \[a=-r\sin ωt × ω\] \[∴a=-ω^2y\] When the particle is at the extreme position i.e. $y=r$, then, \[a=-ω^2r\] ∴Acceleration is maximum at the mean position. When the particle is at the mean position i.e. y=0, then, \[a=-ω^2×0=0\] ∴Acceleration is zero at the mean position.
Time Period
It is the time taken by the object to make a complete round on the circle. We know, \[a=-ω^2y\] Taking magnitude only, \[a=ω^2y\] \[ω=\sqrt{\frac{a}{y}}\] \[\frac{2 π}{T}=\sqrt{\frac{a}{y}}\] \[T=2 π \sqrt{\frac{y}{a}}\] \[∴T=2 π \sqrt{\frac{\text{displacement}}{\text{acceleration}}}\] This gives the time period of the particle executing S.H.M.
Energy of a Particle Executing SHM
In simple harmonic motion, a particle possesses potential energy $(U)$ because of its displacement from the mean position and kinetic energy $(T)$ because of its motion.
Potential Energy
We have, \[a=-ω^2y\] Consider a body of mass $m$ is executing SHM, then, restoring force on the body is, \[F=mω^2y\] When the body moves further infinitesimally small distance $dy$, then the small work done is given by, \[dW=Fdy\] \[dW=mω^2ydy\] Total work done is given by integrating within limits from $0$ to $y$, \[∴W=\int_0^y mω^2ydy\] \[W=\frac{1}{2} mω^2y^2\] This work done is equal to the potential energy $(U)$ of the body, \[∴U=\frac{1}{2} mω^2y^2\]
Kinetic Energy
Let the body have a velocity of $v$, then, \[K.E.=\frac{1}{2}mv^2\text{ ___(a)}\] In S.H.M., \[v=ω\sqrt{r^2-y^2}\text{ ___(b)}\] where, $r =$ amplitude of the S.H.M. and $y =$ displacement from mean position. From $(a)$ and $(b)$, \[∴K.E. (T)=\frac{1}{2}mω^2(r^2-y^2)\]
Total Energy
\[\text{Total Energy (E)}=U+T\] \[E=\frac{1}{2} mω^2y^2+\frac{1}{2}mω^2(r^2-y^2)\] \[E=\frac{1}{2} mω^2r^2\] This gives the total energy of the body executing S.H.M. The total energy remains constant because it does not depend upon the displacement from mean position.
Graphical Representation

When the body is at mean position, $y = 0$, then \[K.E. (T)=\frac{1}{2}mω^2(r^2-0)=\frac{1}{2}mω^2r^2\] and, \[∴U=\frac{1}{2} mω^2 ×0=0\] Thus, kinetic energy is maximum and potential energy is zero at the mean position. When the body is at extreme position, $y = r$, then \[K.E. (T)=\frac{1}{2}mω^2(r^2-r^2)=0\] and, \[∴U=\frac{1}{2} mω^2 r^2\] Thus, potential energy is maximum and kinetic energy is zero at the extreme position.
More on Simple Harmonic Motion
