Simple Pendulum is a heavy point mass suspended by a weightless, inextensible and perfectly elastic string which is able to vibrate freely in the influence of gravity.
Simple Pendulum is known as an ideal pendulum because we cannot have a point mass and a weightless string. In practice, simple pendulum consists of a small heavy metallic bob suspended by a long fine thread from a rigid support.
The point from which the pendulum is suspended is known as the point of suspension. When the bob is pulled to one side of its equilibrium position and released, it swings in a vertical plane under gravity.
The centre of gravity of the pendulum is the centre of gravity of the bob and is known as point of oscillation. The distance between the point of suspension and the point of oscillation is the length of the simple pendulum.
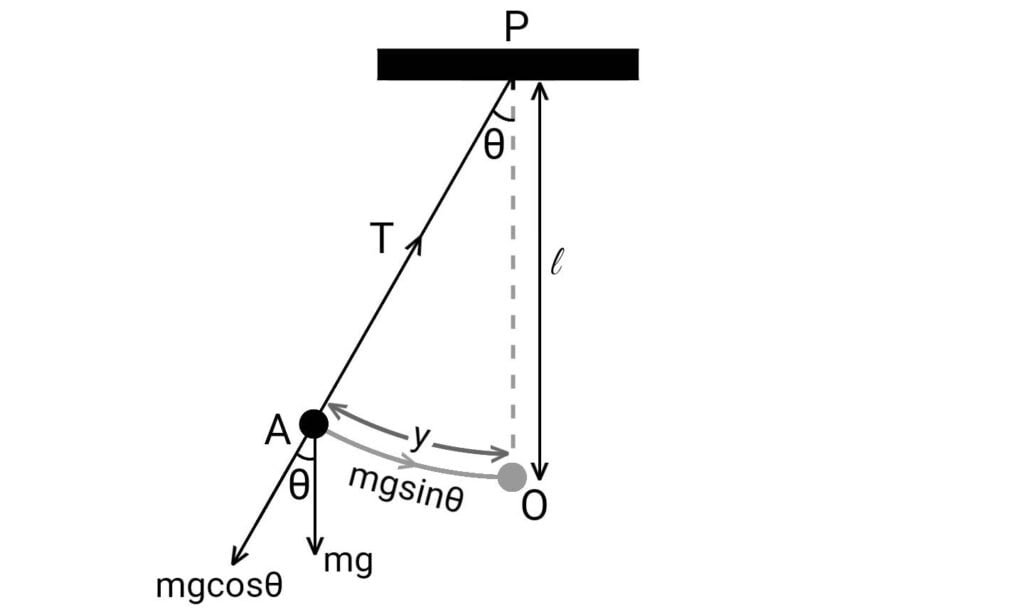
Consider a metallic bob of mass $m$ is suspended by a fine thread of length $l$. Suppose the bob is displaced through angle $θ$ from the equilibrium position such that the arc $OA = y$. Then, \[θ=\frac{y}{l}\]
When the bob is in position $A$, its weight $mg$ acts vertically downwards and the tension $T$ acts along its thread towards the point of suspension.
The weight of the bob can be resolved into two components; $mg\cos θ$ and $mg\sin θ$. Here, $mg\cos θ$ balances the tension $T$ in the string and $mg\sin θ$ acts as a restoring force which brings the bob back to its equilibrium position.
\[F=-mg\sin θ\text{ _____(1)}\]
This restoring force produces acceleration $a$ in the bob.
\[∴ma=-mg\sin θ\]\[a = -\sin θ\]
If $θ$ is small, $\sin θ≈θ$.
\[∴a=-gθ\text{ ___(3)}\]
From $(1)$ and $(3)$,
\[a=-g\cdot\frac{y}{l}\]\[a=-(\frac{g}{l})\cdot y\]\[a∝-y\]
Acceleration in the bob is directly proportional to the displacement from the mean position. So, the motion of the bob is simple harmonic.
Time Period
Time Period is the time taken by the pendulum to complete one oscillation.
\[T=2π\sqrt{\frac{\text{displacement}}{\text{acceleration}}}\]\[T=2π\sqrt{\frac{y}{a}}\]
we have, in magnitude,
\[a=g\cdot\frac{y}{l}\] \[∴T=2π\sqrt{\frac{y}{g\frac{y}{l}}}\]\[T=2π\sqrt{\frac{l}{g}}\]
Seconds Pendulum
A pendulum whose time period is two seconds is known as seconds pendulum.
We have,
\[l=\frac{T^2g}{4π^2}\]
Here, $g=9.8\text{ m/s}^2$ and $T=2\text{ sec}$, then,
\[l=\frac{2²* 9.8}{4* 9.87}\]\[∴l=0.993 \text{ m}\]
∴Length of a second’s pendulum is $0.993\text{ m}$.
More on Simple Harmonic Motion
