Every liquid at rest, tends to have a minimum surface area. So, a liquid drop, free from external forces like gravity, always tends to have spherical shape. Because, for a given volume, sphere has the least surface area. While doing so, the free surface behaves as if covered by a stretched membrane, having tensions in all directions parallel to the surface. This tension in the free surface of liquid at rest is called the surface tension.
The property of a liquid by virtue of which it tends to have a minimum surface area is known as surface tension. The surface of the liquid, due to surface tension, behaves as a stretched membrane.
Table of Contents
Some Definitions
Types of Molecular Forces
Force of adhesion or Adhesive force
It is the force of attraction between the molecules of different substances.
For example, water wets the surface of a glass container. This is due to the adhesive force between the molecules of glass and water. Similarly, while writing, graphite from lead pencil sticks to the paper due to the adhesive force between the molecules of graphite and paper. Fevicol, cement, etc. are useful for gluing two surfaces together again on account of adhesive force.
Force of cohesion or Cohesive force
It is the force of attraction amongst the molecules of a same substance.
Mercury does not wet the surface of a glass container because the cohesive forces amongst the molecules of mercury is greater than the adhesive forces between the molecules of mercury and glass.
The definite shape and size of solid is due to strong cohesive force amongst their molecules. Liquid have a definite volume, but no definite shape. Therefore, cohesive force in case of liquids must be weaker than the cohesive force in case of solids. On the other hand, gases have neither fixed volume nor fixed shape. Therefore, cohesive forces amongst the gaseous molecules are least.
The cohesive and adhesive forces are Vander Wall forces. These forces are different from ordinary gravitational forces and they do not obey inverse square law. The cohesive or adhesive force varies inversely as the seventh power of distance between the molecules i.e. the cohesive or adhesive force increases rapidly as the distance between the molecules decreases.
Molecular Range
It is the maximum distance upto which a molecule can exert measurable attractive forces on other molecule. It is different for different substances. The order of molecular range is $10^{-9}\;\text{m}$ in solids and liquids.
Sphere of Influence
A sphere drawn around a molecule, taking the molecule as its centre and the molecular range as its radius, is called sphere of influence. All the molecules in this sphere attract other molecules at centre.
Surface film
Surface film is the top most layer of the liquid at rest with thickness equal to the molecular range.
Molecular Explanation of Surface Tension
Surface tension can be explained by intermolecular force of attraction between liquid molecules.
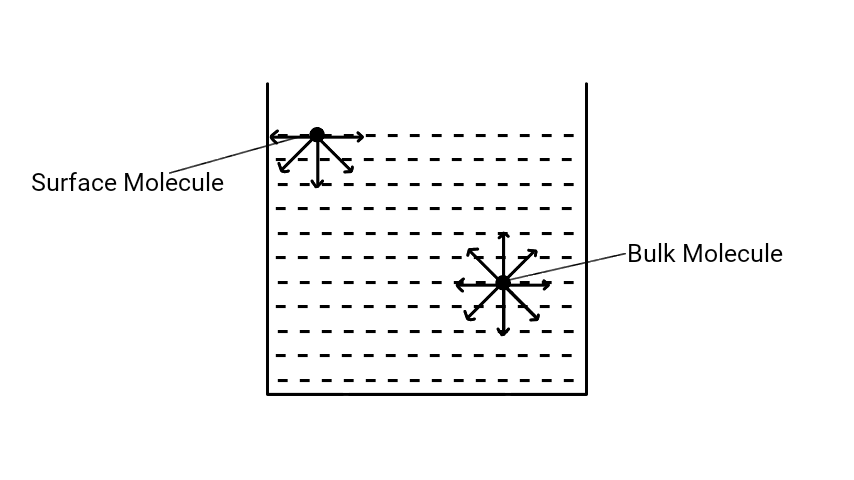
The bulk molecules experience the force of attraction from every sides. So, the net force of attraction on the bulk molecules remain balanced. But in case of surface molecules, the molecules experience only downward force of attraction. Due to this downward pull on the surface molecules, the surface of the liquid tends to contract and the surface behaves as a stretched membrane. This downward force on the surface molecules is surface tension.
Hence, we conclude that no resultant force acts on a molecule which lies below the surface film. But, a resultant downward cohesive force acts on all those molecules lying in the surface film. This cohesive force increases as we move from the bottom of the surface film to its top. This means, to take a molecule into the surface film from anywhere below it, some work has to be done against the downward cohesive force. This work done appears as potential energy of the molecule.
Thus, all the liquid molecules in the surface film possess potential energy i.e. the surface film has potential energy. The greater is the number of molecules in the surface film, the larger is the potential energy of the surface film.
We know that every system in the equilibrium state has minimum potential energy. Hence, to attain the equilibrium state, the surface film also tends to have the minimum potential energy. This will be so if the number of molecules in the surface film are minimum. For this, the surface film should have minimum volume, which would be so if the surface film has least surface area. In trying to acquire least surface area, the surface film tends to contract and hence, behaves as a stretched membrane.
Calculation of Surface Tension
Imagine a line AB drawn tangentially anywhere at the surface of liquid at rest. Then, the tangential force acting per unit length of this line at right angle gives the surface tension of the liquid.

\[γ=\frac{F}{l}\] where,
$γ =$ surface tension
$F =$ force acting along the imaginary line
$l =$ length of imaginary line
Therefore, surface tension of a liquid at rest is measured as the force acting on unit length of an imaginary line drawn tangentially anywhere on the free surface of the liquid. It acts at right angles to this line on both the sides and along tangent to the liquid surface.
The SI unit of surface tension of $\text{N/m}$.
Some Examples of Surface Tension
- Rain drops are spherical in shape. Because they tend to attain minimum surface area.
- Small insects can walk freely on the surface of water.
- A small needle, if gently placed on the surface of water, floats on water even though its density is very large than water. But if one end of the needle breaks the surface, then the needle will sink.

- Capillary action is due to the surface tension. When the adhesive force is greater than cohesive force, then the liquid rises in the capillary tube and forms concave meniscus. As shown in above figure, water forms concave meniscus in a capillary tube. But when the cohesive force is greater than adhesive force, then the liquid falls down in the capillary tube and forms convex meniscus. As shown in above figure, mercury forms convex meniscus in a capillary tube.
More on Surface Tension
