Robert Andrew (R.A.) Millikan determined the value of the basic unit of charge $(e)$ in 1909 by the use of oil drop. This method is called Millikan’s oil drop experiment.
Principle
The main principle of this experiment is the Stoke’s law in viscosity. In this experiment, the motion of a nonvolatile and viscous small spherical drop is observed under following two cases;
1. Motion under the effect of gravity alone.
2. Motion under the combined effect of gravity and electric field.
Nonvolatile and viscous materials having low vapour pressure like clock oil, glycerine, etc. is used because Stoke’s law holds good for them at constant temperature.
The Millikan’s oil drop experiment consists of a doubled wall chamber as shown in figure.
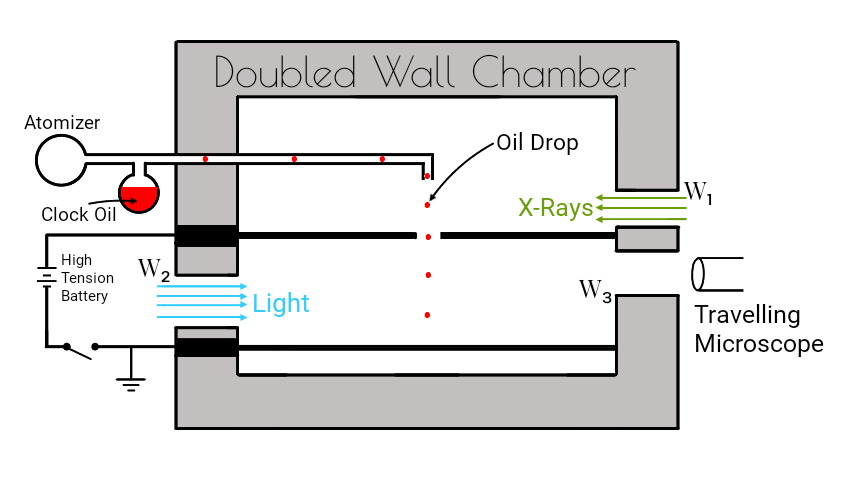
The apparatus consists of an atomizer which sprays fine oil droplets of density $ρ$. It consists two metal plates $A$ and $B$ separated by a small distance by means of an insulator. A high p.d. of order $10,000 V$ is established between the plates by connecting the plates to a high tension battery. The upper plate $A$ has a central hole $H$ from which the droplets pass.
A source of light is allowed to throw light from the window $W_2$ to illuminate he falling drops. X-rays are allowed to enter through the window $W_1$ to ionize the air inside so that ions can stick on the droplets. A travelling microscope $(T)$ is used to study the motion of an oil drop.
Case I: The Motion Under The Effect Of Gravity Alone
Initially, the electric field between the plates $A$ and $B$ is not establish. Under this condition, the oil drop falls under gravity experiencing upthrust. Let the radius of the observed oil drop of density $ρ$ be $r$. Then, \[\text{Volume of the oil drop}=\frac{4}{3}πr^3\] and, \[\text{Weight of the oil drop (W)}=\frac{4}{3}πr^3ρg\]
If $σ$ is the density of air, then, according to Archimedes’ principle, Upthrust of air on the drop $=$ Weight of air displaced \[\text{Upthrust on the drop (U)}=\frac{4}{3}πr^3σg\]
Due to air resistance, after some time, the falling drop will attain terminal velocity $v_1$. If $η$ is the coefficient of viscosity of air then from Stoke’s law, the viscous force $F_1$ on the drop in upward direction is, \[F_1=6πηrv_1\]
Under Equilibrium condition of the drop, \[W=U+F_1\] \[\frac{4}{3}πr^3ρg=\frac{4}{3}πr^3σg+6πηrv_1\] \[6πηrv_1=\frac{4}{3}πr^3(ρ-σ)g\text{ __(1)}\] \[r=\sqrt{\frac{9ηv_1}{2(ρ-σ)g}}\text{ __(2)}\]
Case II: The Motion Under The Combined Effect Of The Gravity And The Electric Field
An electric field $E$ is applied between the plates $A$ and $B$. If $V$ is the p.d. between the plates separated by distance $d$, then, \[E=\frac{V}{d}\] Under electric field, the drop moves upward with terminal velocity $v_2$.
If $q$ is the total charge on the drop, then the upward electric force is, \[F_e=qE\] The viscous force $F_2$ acting downward on the drop is, \[F_2=6πηrv_2\]
Under equilibrium condition of the liquid drop, \[W+F_2=F_e+U\] \[\frac{4}{3}πr^3ρg+6πσrv_2=qE+\frac{4}{3}πr^3σg\] \[qE-\frac{4}{3}πr^3(ρ-σ)g=6πηrv_2\] \[qE-6πηrv_1=6πηrv_2\] \[qE=6πηr(v_1+v_2)\] \[q\frac{V}{d}=6πηr(v_1+v_2)\] \[q=\frac{6πηr(v_1+v_2)d}{V}\] \[q=\frac{6πηd(v_1+v_2)}{V}\sqrt{\frac{9ηv_1}{2(ρ-σ)g}}\text{ __(3)}\]
By using this formula, the charge $q$ on the drop can be calculated. Millikan repeated the experiment for many different droplets and found that all the charges were integral multiple of a unique value of $1.6×10^{-19}$ $C$ which is the lowest charge in Nature. Hence, Millikan concluded that the charge of an electron is $-1.6×10^{-19}$ $C$.
- In Millikan’s original experiment, he allowed drops to move down with velocity $v_2$ on applying electric field. In this case, $v_1$ and $v_2$ has opposite direction and equation $(3)$ becomes, \[q=\frac{6πηd(v_1-v_2)}{V}\sqrt{\frac{9ηv_1}{2(ρ-σ)g}}\]
- Later on, he adjusted electric field so that the drop remained stationary i.e. $v_2=0$, then equation $(3)$ becomes, \[q=\frac{6πηd(v_1)}{V}\sqrt{\frac{9ηv_1}{2(ρ-σ)g}}\]
