A hyperbola is the locus of a point in a plane such that the difference of its distances from two fixed points is a constant. A conic section whose eccentricity is greater than $1$ is a hyperbola.
Standard Equation
Let the two fixed points (called foci) be $S(c,0)$ and $S'(-c,0)$. The midpoint between the fixed points is the centre of the hyperbola. In this case, the centre is at the origin. Take any point $P(x,y)$ on the hyperbola. Then \[\begin{array}{c}\text{if}\;PS>PS’,&PS-PS’=\text{Constant} \\ \text{if}\;PS’>PS, &PS’-PS=\text{Constant}\end{array}\]
\[\text{Let}\;PS-PS’=2a\]
By using distance formula, \[\sqrt{(x+c)^2+y^2}-\sqrt{(x-c)^2+y^2}=2a\] \[(x+c)^2+y^2=4a^2+(x-c)^2+y^2+4a\sqrt{(x-c)^2+y^2}\] \[4cx-4a^2=4a\sqrt{(x-c)^2+y^2}\] \[(cx-a^2)^2=a^2[(x-c)^2+y^2]\] \[a^2x^2-c^2x^2+a^2y^2=a^4-a^2c^2\] \[x^2(a^2-c^2)+a^2y^2=a^2(a^2-c^2)\] \[\therefore\frac{x^2}{a^2}+\frac{y^2}{a^2-c^2}=1\]
Since the difference of two sides of a triangle is less than the third, we have \[PS-PS'<SS’\] \[\text{i.e.}\;2a<2c\Rightarrow a<c\] \[\therefore a^2-c^2\;\text{is negative.}\]
Let $b^2=c^2-a^2$ then the equation of the hyperbola becomes \[\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\]
This is the equation of the hyperbola in standard form.
Graph
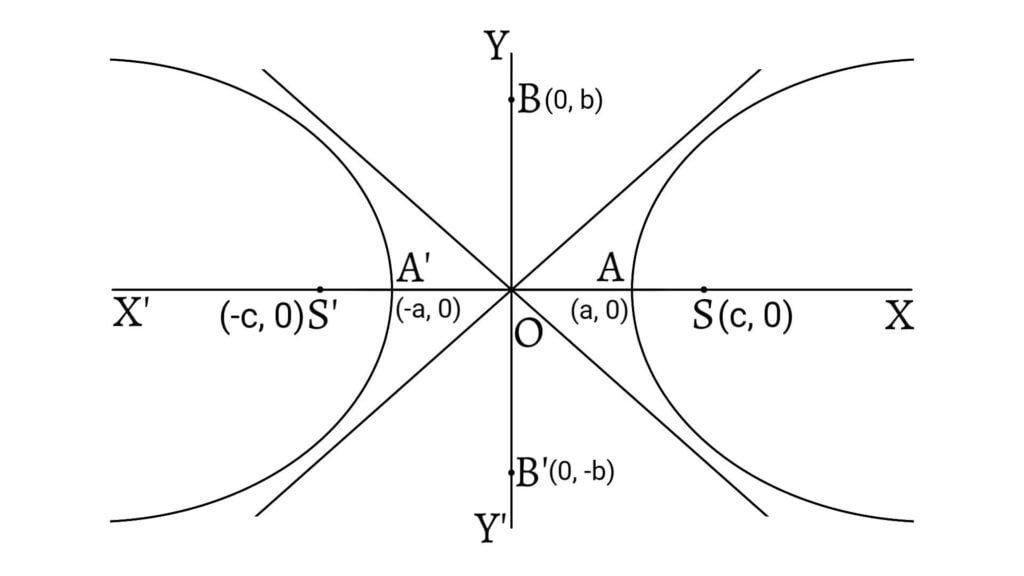
The graph of a hyperbola consists of two branches that go to infinity. The two straight lines $y=\frac{b}{a}x$ and $y=-\frac{b}{a}x$ are asymptotes to the hyperbola. That is, the distance of a point on the hyperbola from the line tends to zero as the point moves to infinity along the curve.
The vertices of the hyperbola are $A(a,0)$ and $A'(-a,0)$. The line $AA’$ joining the vertices $A$ and $A’$ is called the transverse axis and its length is $2a$. The line $BB’$ perpendicular to the transverse axis such that $OB=OB’=b$ is called the conjugate axis and its length is $2b$.
The eccentricity $e$ of the hyperbola is defined as $e=\frac{c}{a}$. \[\therefore e=\frac{c}{a}=\frac{\sqrt{a^2+b^2}}{a}=\sqrt{1+\frac{b^2}{a^2}}\]
Since $c>a$, $e$ is greater than $1$. The coordinates of the foci are $(\pm ae,0)$. The equation of directrix is $x=\pm\frac{a}{e}$. Also, the length of the latus rectum is $\frac{2b^2}{a}$.
Conjugate Hyperbola
The hyperbola whose transverse axis is along the y-axis and the conjugate axis along the x-axis is called the conjugate hyperbola. Its equation is \[\frac{y^2}{b^2}-\frac{x^2}{a^2}=1\] \[\text{or,}\;\frac{x^2}{a^2}-\frac{y^2}{b^2}=-1\]
Its vertices are $A(0,b)$ and $A'(0,-b)$. The eccentricity $e$ is given by \[e=\frac{c}{b}=\sqrt{1+\frac{a^2}{b^2}}\]
The coordinates of the foci are $(0,\pm be)$. The equation of directrix is $y=\pm\frac{b}{e}$. Also, the length of the latus rectum is $\frac{2a^2}{b}$.
Hyperbola whose Asymptotes are the Axes of Coordinates
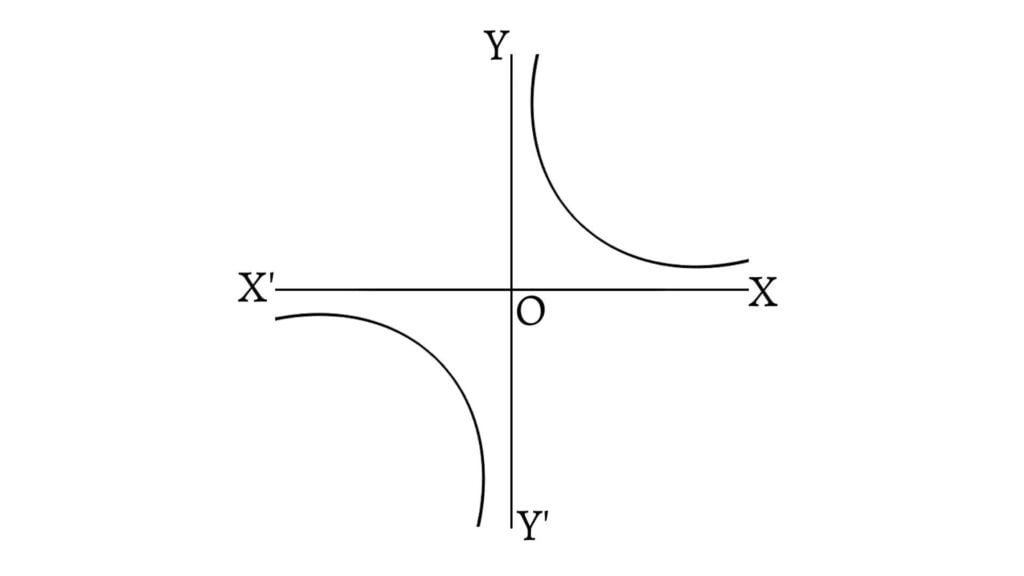
If the foci of a hyperbola be at $S(a,a)$ and $S(-a,-a)$ and if $P(x,y)$ by any point on the hyperbola, then \[\sqrt{(x+a)^2+(y+a)^2}-\sqrt{(x-a)^2+(y-a)^2}=2a\] \[4ax+4ay-4a^2=4a\sqrt{(x-a)^2+(y-a)^2}\] \[x+y-a=\sqrt{(x-a)^2+(y-a)^2}\] \[(x+y-a)^2=(x-a)^2+(y-a)^2\] \[\therefore 2xy=a^2\] \[\text{or,}\;xy=c^2\; \text{where}\:c^2=\frac{a^2}{2}\] \[\therefore xy=c^2\]
The asymptotes of such hyperbola are the axes of coordinates as shown in the above graph.
Equation of the Hyperbola centered at $(h,k)$
The equation of a hyperbola whose centre is at $(h,k)$ is given by \[\frac{(x-h)^2}{a^2}-\frac{(y-k)^2}{b^2}=1\]
Its vertex is $(h\pm a,k)$ and focus $(h\pm ae,k)$. The eccentricity $e$ is given by \[e=\sqrt{1+\frac{b^2}{a^2}}\]
The equation of directrix is $x=h\pm\frac{a}{e}$ and the length of the latus rectum is $\frac{2b^2}{a}$.
Similarly, we can evaluate the hyperbola given by the equation \[\frac{(x-h)^2}{a^2}-\frac{(y-k)^2}{b^2}=-1\]
Its vertex is $(h,k\pm b)$ and focus $(h,k\pm be)$. The eccentricity $e$ is given by \[e=\sqrt{1+\frac{a^2}{b^2}}\]
The equation of directrix is $y=k\pm\frac{b}{e}$ and the length of the latus rectum is $\frac{2a^2}{b}$.
Previous: Ellipse