Section Formulae

In some cases, we have to determine the coordinates of a point which divides the given two points in a given ratio. Then, there can be two such cases; either the point divides the line internally or externally. The formulae giving the coordinates of such points of division are called section formulae.

Internal Division

Let $P(x_1,y_1,z_1)$ and $Q(x_2,y_2,z_2)$ be any two points in the three dimensional space. Suppose a point $R(x,y,z)$ divides the join of $P$ and $Q$ in the ratio $m:n$ internally as shown in the figure given below.

From $P$, draw $PL$ perpendicular to xy-plane and then draw parallel lines $QM$ and $RN$ cutting the xy-plane at $M$ and $N$ respectively. $L$, $N$ and $M$ all lie in the xy plane and in the same line $LM$. Also, $QM$ and $RN$ are perpendicular to the plane. A line $PN’M’$ drawn parallel to $LNM$ cuts $RN$ and $QM$ perpendicular at $N’$ and $M’$ respectively.

\[MM’=NN’=LP=z_1\] \[N’R=NR-NN’=z-z_1\] \[M’Q=MQ-MM’=z_2-z_1\] Since $N’R//M’Q$, $\Delta PN’R$ and $\Delta PM’Q$ are similar. \[\therefore\frac{N’R}{M’Q}=\frac{PR}{PQ}\] \[\frac{z-z_1}{z_2-z_1}=\frac{m}{m+n}\] \[(m+n)(z-z_1)=m(z_2-z_1)\] \[z=\frac{mz_2-mz_1}{m+n}+z_1\] \[z=\frac{mz_2+nz_1}{m+n}\] Similarly, \[y=\frac{my_2+ny_1}{m+n}\;\text{ and }\;x=\frac{mx_2+nx_1}{m+n}\] Then, the coordinates of $R$ are \[\left(\frac{mx_2+nx_1}{m+n},\frac{my_2+ny_1}{m+n},\frac{mz_2+nz_1}{m+n}\right)\]

External Division

Let $P(x_1,y_1,z_1)$ and $Q(x_2,y_2,z_2)$ be any two points in the three dimensional space. Suppose a point $R(x,y,z)$ divides the join of $P$ and $Q$ in the ratio $m:n$ externally as shown in the figure given below.

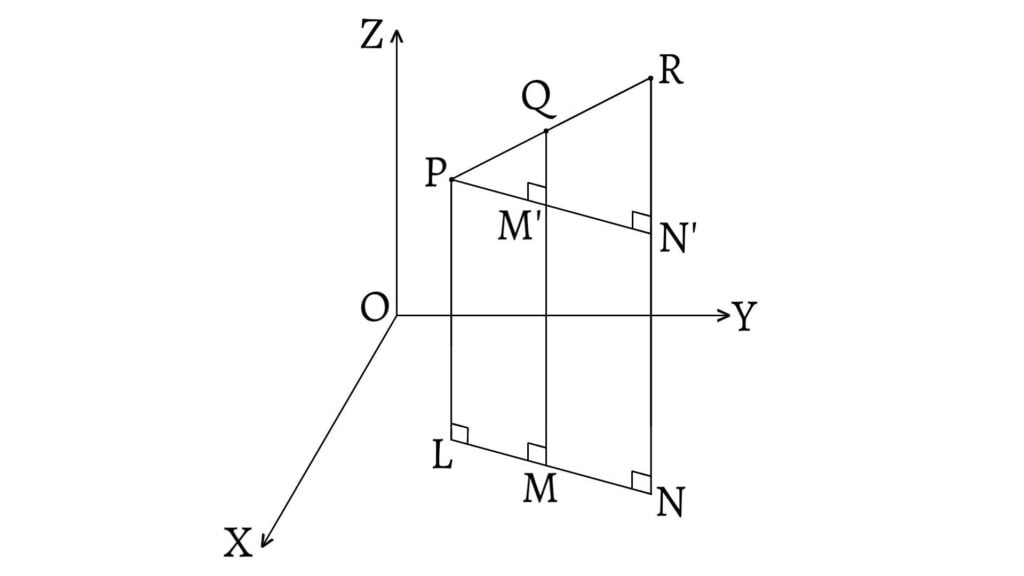
From $P$, draw $PL$ perpendicular to xy-plane and then draw parallel lines $QM$ and $RN$ cutting the xy-plane at $M$ and $N$ respectively. $L$, $M$ and $N$ all lie in the xy plane and in the same line $LN$. Also, $QM$ and $RN$ are perpendicular to the plane. A line $PM’N’$ drawn parallel to $LMN$ cuts $RN$ and $QM$ perpendicular at $N’$ and $M’$ respectively.

\[MM’=NN’=LP=z_1\] \[N’R=NR-NN’=z-z_1\] \[M’Q=MQ-MM’=z_2-z_1\] Since $N’R//M’Q$, $\Delta PN’R$ and $\Delta PM’Q$ are similar. \[\therefore\frac{N’R}{M’Q}=\frac{PR}{PQ}\] \[\frac{z-z_1}{z_2-z_1}=\frac{m}{m-n}\] \[(m-n)(z-z_1)=m(z_2-z_1)\] \[z=\frac{mz_2-mz_1}{m-n}+z_1\] \[z=\frac{mz_2-nz_1}{m-n}\] Similarly, \[y=\frac{my_2-ny_1}{m-n}\;\text{ and }\;x=\frac{mx_2-nx_1}{m-n}\] Then, the coordinates of $R$ are \[\left(\frac{mx_2-nx_1}{m-n},\frac{my_2-ny_1}{m-n},\frac{mz_2-nz_1}{m-n}\right)\]

Cor.1 The coordinates of the middle point of the line segment joining the points $P(x_1,y_1,z_1)$ and $Q(x_2,y_2,z_2)$ are \[\left(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2},\frac{z_1+z_2}{2}\right)\]

Cor.2 The coordinates of the point that divides the line segment joining the points $P(x_1,y_1,z_1)$ and $Q(x_2,y_2,z_2)$ in the ratio $\lambda:1$ are \[\left(\frac{\lambda x_2+x_1}{\lambda+1},\frac{\lambda y_2+y_1}{\lambda+1},\frac{\lambda z_2+z_1}{\lambda+1}\right)\]

---

---