Circle
Consider a fixed point. Then, a circle is a closed curve around the point such that every point on the curve is at a constant distance from that point. In terms of locus, a circle may be defined as the locus of a point which moves so that its distance from a fixed point is constant.
The fixed point is called the centre and the constant distance is called the radius of the circle.
Equation of a Circle
Centre at the origin (Standard form)
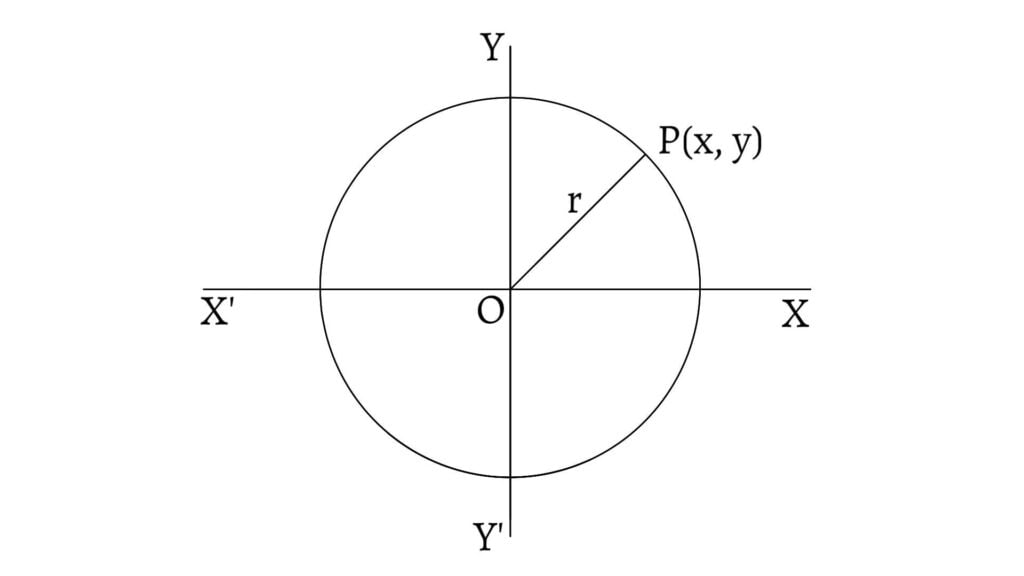
Let
Centre at any point (Central form)

Let
Equation of the circle touching the x-axis

Let
Equation of the circle touching the y-axis

Let
Equation of the circle touching both axes

Let
General equation of the circle
Consider an equation
Comparing equation
- If
- If
- If
The general equation of second degree
Circle with a given diameter (Diameter form)
Let

Next: A Point, a Line and a Circle
