Power

Power is the time rate of doing work. It is the work done per second or energy spent or used per second.

$$\text{Power}=\frac{\text{Work done}}{\text{Time taken}}$$

$$=\frac{\text{Force × Displacement}}{\text{Time taken}}$$

$$=\text{Force × Velocity}$$

$$\therefore P=F\times v$$

The SI unit of power is Watt $(W)$.

$$1W=1J{s}^{-1}={10}^7\text{ Erg }{s}^{-1}$$

Larger Units of Power

$$1\text{ Horsepower (HP)}=746\text{ Watts}$$

$$1\text{ kW}=1000{\text{ W (10}}^3\text{ W)}$$

$$1\text{ MW}=1000000{\text{ W (10}}^6\text{ W)}$$

If one joule of work is done in the time of one second, then, $$P=\frac{1J}{1s}$$ $$P=1W$$ Thus, if a body can do one joule of work in one second then the body is said to have $1$ watt of power.

Different electrical appliances are labelled with different watt of power. A bulb labelled with $100$ watt means that the bulb can convert $100$ joule of electrical energy into heat and light energy in $1$ second.

---

Q. Calculate the power of a pump which can lift $300$ $\text{kg}$ of water through a vertical height of $4$ $\text{m}$ in $10$ $\text{sec}$. (Take $g=10$ ${\text{ms}}^{-2}$)

$$\text{Work done}=mgh$$ $$=300\times 10\times 4$$ $$=12000J$$ $$\text{and, Time taken}=10\text{ secs}$$ Thus, $$\text{Power of the pump}=\frac{\text{Work done}}{\text{Time taken}}$$ $$=\frac{12000}{10}$$ $$=1200W$$

---

Q. Find the power of an engine which can travel at the rate of $27$ $\text{km/hr}$ up an incline of $1$ in $100$, the mass of the engine and the load being $10$ $\text{metric tonnes}$ and the resistance due to friction, etc. being $10$ $\text{kg wt. per metric tonne}$. (Take $g=10$ ${\text{ms}}^{-2}$)

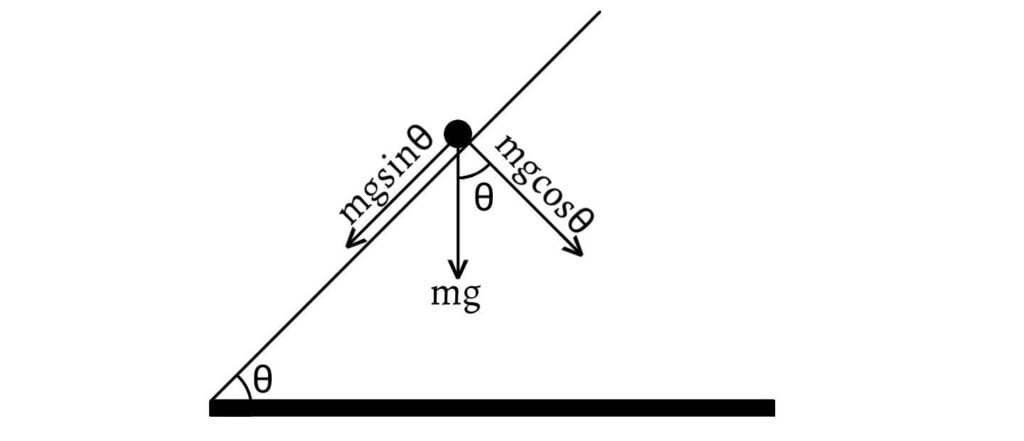
Mass of the Engine and load $(m)$ $$=10\text{ metric tonnes}$$ $$=10000\text{ kg}$$ Resistance due to friction, etc. $$=10\text{ kg wt. per metric tonnes}$$

Resistance due to friction, etc. for the mass of the engine and load $$=100\text{ kg wt.}$$ $$=100\times 10\text{ N}$$ $$=1000\text{ N}$$

Thus, $$\text{Total Opposing Force}=mg\sin \theta +\text{Resistance}$$ $$=10000\times 10\times \frac{1}{100}+1000$$ $$=2000\text{ N}$$ and, $$\text{Velocity}=27\text{ km/hr}$$ $$=7.5\text{ m/s}$$

Therefore, $$\text{Power of the engine}=\text{Force}\times \text{Velocity}$$ $$=2000\times 7.5$$ $$=15000\text{ W}$$ $$=15\text{ kW}$$

---

More on Work, Energy And Power

• Work
• Energy