Dispersion of light is the phenomenon of splitting up of while light into its constituent colours.
White light consists of seven different colours. When a beam of light falls on a prism, the light emerging from the prism consists of seven colours VIBGYOR (Violet, Indigo, Blue, Green, Yellow, Orange, Red). The violet colour deviates maximum while the red colour has the least deviation.
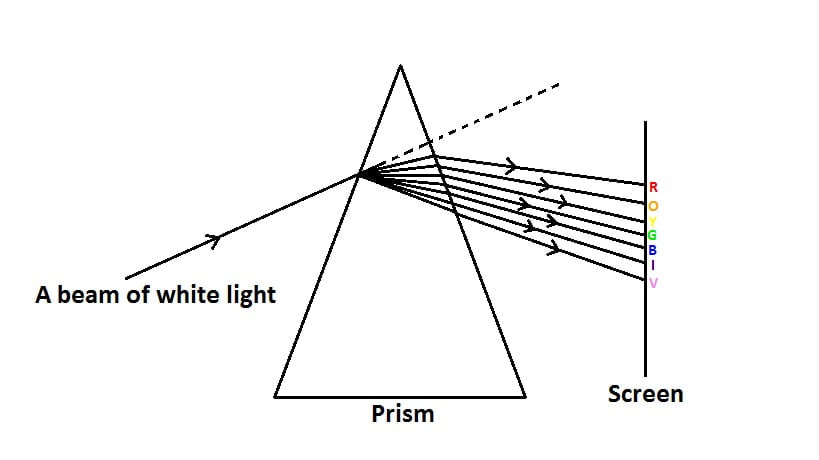
The band of colour produced on the screen is known as spectrum.
Cause of Dispersion
Different colours of light have different wavelengths. If a light has wavelength $λ$, then, Cauchy’s formula for the refractive index $μ$ of the material is, \[μ=a+\frac{b}{λ^2}+\frac{c}{λ^4}\] where $a$, $b$ and $c$ are the constants for the material.
Wavelength of violet light is least while the wavelength of red light is maximum. So, according to the above relation, we have, \[μ_v>μ_r\]
Deviation produced by small angle prism is, \[δ=A(μ-1)\] \[\text{Since }μ_v>μ_r\text{,}\] \[δ_v>δ_r\]
Thus, violet colour deviates maximum while the red colour deviates least. Similarly, other colours also deviate depending on their wavelengths.
Angular Dispersion
Consider a prism of small angle $A$. Let a beam of white light is incident on the prism.
Angular dispersion is defined for any two emergent rays. The difference in deviations suffered by any two colours in passing through the prism is defined as the angular dispersion for the two rays.

From above figure, $θ$ is the angular dispersion for red ray and violet ray. \[θ=δ_v-δ_r\text{ __(a)}\]
Let $μ_v$ and $μ_r$ be the refractive index of the material of the prism for violet ray and red ray respectively. Then, \[δ_v=A(μ_v-1)\text{ __(b)}\] \[δ_r=A(μ_r-1)\text{ __(c)}\]
From $(a)$, $(b)$ and $(c)$, \[θ=A(μ_v-1)-A(μ_r-1)\] \[θ=Aμ_v-A-Aμ_r+A\] \[θ=A(μ_v-μ_r)\text{ __(1)}\] This gives the angular dispersion for violet ray and red ray.
Dispersive Power
We take yellow light as the mean light.

Let $μ$ be the refractive index of the material of the prism for the mean light and $δ$ be the deviation suffered by it. \[∴δ=A(μ-1)\text{ __(2)}\]
Dividing $(1)$ by $(2)$, \[\frac{θ}{δ}=\frac{A(μ_v-μ_r)}{A(μ-1)}\] \[\frac{θ}{δ}=\frac{μ_v-μ_r}{μ-1}\] \[∴ω=\frac{θ}{δ}=\frac{μ_v-μ_r}{μ-1}\]
This $ω$ is called dispersive power of the material of the prism for the violet ray and the red ray.
Thus, dispersive power of a material for any two colours can be defined as the ratio of the angular dispersion for these two colours to the deviation suffered by the mean light.
[Also See: Why is the Sky Blue?]
