Ammeter
An ammeter is a device which is used to measure current in an electric circuit. A galvanometer has very low resistance so it shows full scale deflection even when a small current is passed through it. If a large current is passed through it, then large amount of heat produced can damage it and also large deflection may break the pointer. So, a small resistance (known as shunt) is connected in parallel with the galvanometer. [Parallel Combination of Resistors]
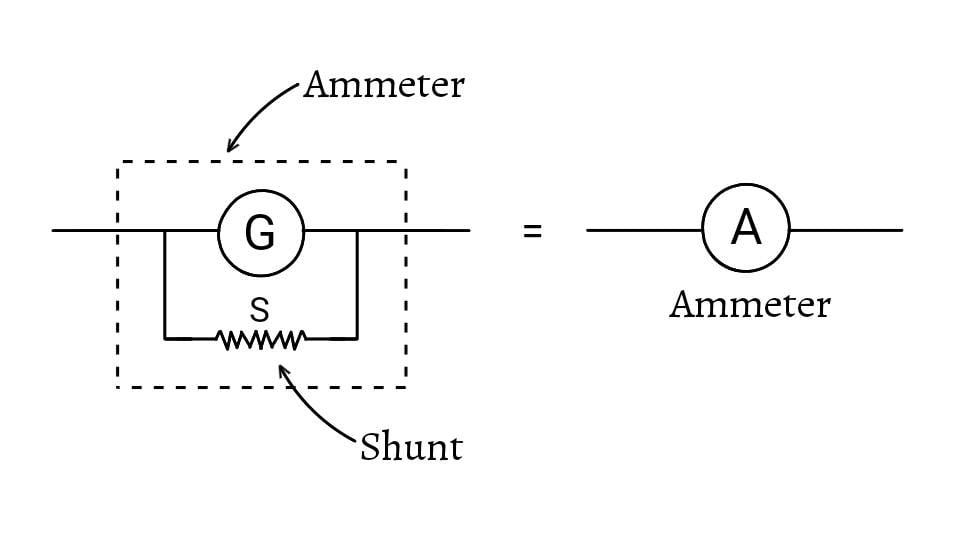
This shunted galvanometer is called ammeter. This ammeter is joined in series in the circuit. So, a low resistance galvanometer is an ammeter. An ideal ammeter has zero resistance (which is not possible in practice).
An ammeter is always connected in series in the circuit because it is a current measuring device, so the current, which is to be measured, should pass through the ammeter for which it should be in series in the circuit.
An ammeter has a low resistance because it is connected in series in a circuit, and the current, which is to be measured, passes through it. So, the resistance of the ammeter should not affect the current and for that an ammeter should have very low resistance.
Conversion of a Galvanometer into an Ammeter
To convert a galvanometer into an ammeter of range $(0-I)$ ampere, a shunt (resistor of small resistance) is connected in parallel to the galvanometer. [Parallel Combination of Resistors]
The value of resistance of shunt determines the range of the ammeter.
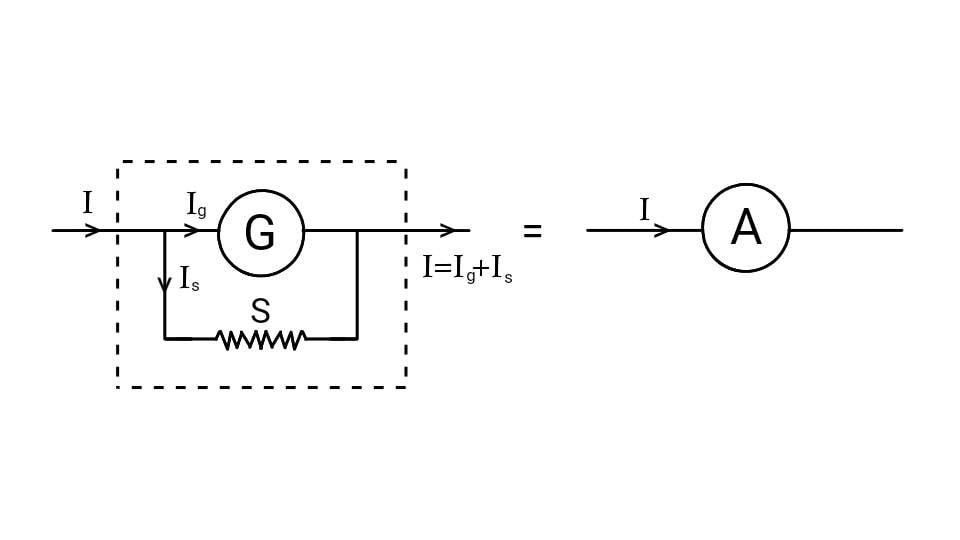
Let the resistance of the galvanometer be $G$ and the maximum current required to show full deflection in the galvanometer be $I_g$. Now, we have to convert it into an ammeter which shows full deflection for a large current $I$. Let the resistance of the shunt be $S$.
Since the galvanometer and the shunt are connected in parallel to each other, the potential difference across the galvanometer is equal to the potential difference across the shunt i.e.
\[\text{p.d. across galvanometer}=\text{p.d. across shunt}\]
\[I_gG=(I-I_g)S\]
\[S=\frac{I_g}{I-I_g}G\]
By using this formula, the value of shunt can be calculated.
And, the equivalent resistance of the ammeter is given by,
\[\frac{1}{R}=\frac{1}{G}+\frac{1}{S}=\frac{S+G}{GS}\]
\[R=\frac{GS}{S+G}\]
The value of $G$ is large as compared to $S$, so the equivalent resistance of the ammeter is very low than that of galvanometer.
Voltmeter
A voltmeter is a device which is used to measure voltage in an electric circuit. It is connected in parallel across the points in the circuit. To measure the voltage across the points, the voltmeter should draw negligible current which is only possible if the voltmeter has very high resistance. So, a high resistance (multiplier) is connected in series with a galvanometer to make it a voltmeter. [Series Combination of Resistors]
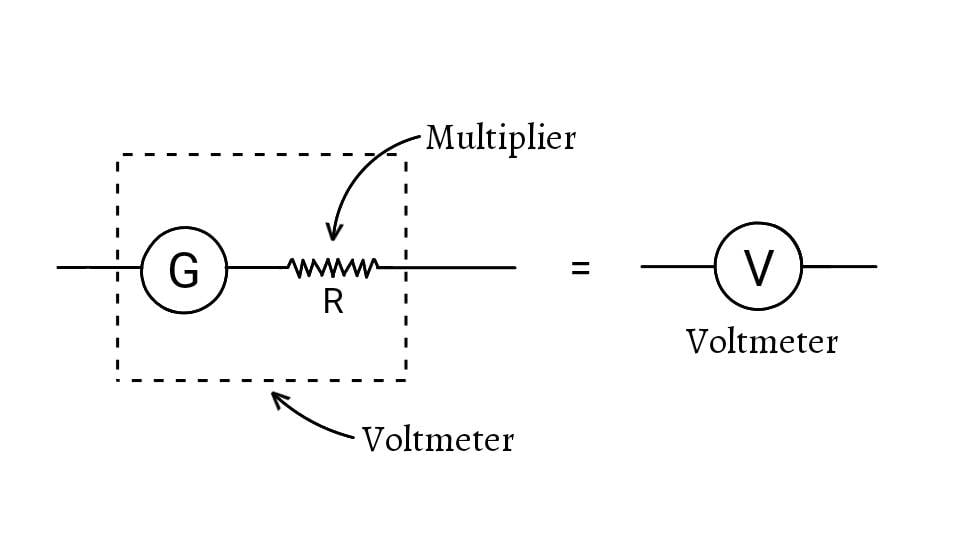
A high resistance galvanometer is a voltmeter. An ideal voltmeter has infinite resistance (which is not possible in practice).
A voltmeter is always connected in parallel in the circuit because it is a voltage measuring device. To measure the voltage across the load resistance, it should be put in such a way that it does not affect the current in the load resistance which is only possible when it is connected in parallel. To draw negligible current, a voltmeter has very high resistance.
Conversion of a Galvanometer into a Voltmeter
To convert a galvanometer into a voltmeter of range $(0-V)$ volts, a multiplier (resistor of high resistance) is connected in series to the galvanometer. The value of resistance of multiplier determines the range of the voltmeter. [Series Combination of Resistors]

Let the resistance of the galvanometer be $G$ and the maximum current required to show full deflection in the galvanometer be $I_g$. Let the resistance of the multiplier be $R$.
Since the multiplier is connected in series with the galvanometer, it also has the same current $I_g$.
\[V=I_g(G+R)\]
\[G+R=\frac{V}{I_g}\]
\[R=\frac{V}{I_g}-G\]
This formula can be used to calculate the value of resistance of multiplier.
The equivalent resistance of the voltmeter is given by,
\[R_{\text{eq}}=G+R\]
The value of $R_{\text{eq}}$ is large with respect to $G$. So, a voltmeter is a high resistance galvanometer.
