Parabola

The locus of a point which is equidistant from a fixed point (called the focus) and a fixed line (called the directrix) is called a parabola.

Equation of a Parabola (Standard Form)

Let $S$ be the focus and $ZM$ be the directrix of the parabola. $SZ$ is drawn perpendicular to $ZM$. Let $A$ be the middle point of $SZ$ so that $SA=AZ$. Then, $A$ is the vertex and $ZAS$ is the axis of the parabola.

To determine the equation of a parabola in the standard form, take the vertex $A$ at the origin, the focus $S$ on the x-axis so that the axis of the parabola is the x-axis and the directrix is parallel to y-axis.

Let $AS=a$. Then the coordinates of $Z$, $A$ and $S$ are $(-a,0)$, $(0,0)$ and $(a,0)$ respectively. The equation of the directrix is $\:x+a=0$. [Equations of Straight Lines Parallel to the Axes (Some Fundamental Formulae)]

Let $P(x,y)$ be any point on the parabola. Join $PS$ and draw $PM\perp ZM$. Then, from the definition of parabola, \[PS=PM\] \[PS^2=PM^2\] \[(x-a)^2+y^2=(x+a)^2\] \[\therefore y^2=4ax\]

This is the standard form of a parabola.

Special Cases

If $a$ is positive, $y^2=4ax$ is a parabola whose axis is the x-axis and the curve lies to the right side of the y-axis. If $a$ is negative, $y^2=-4ax$ lies to the left side of the y-axis.

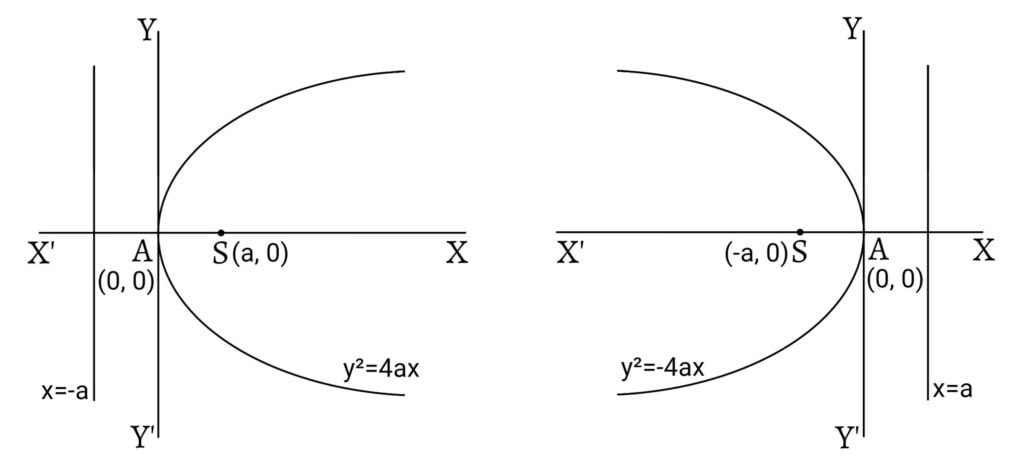
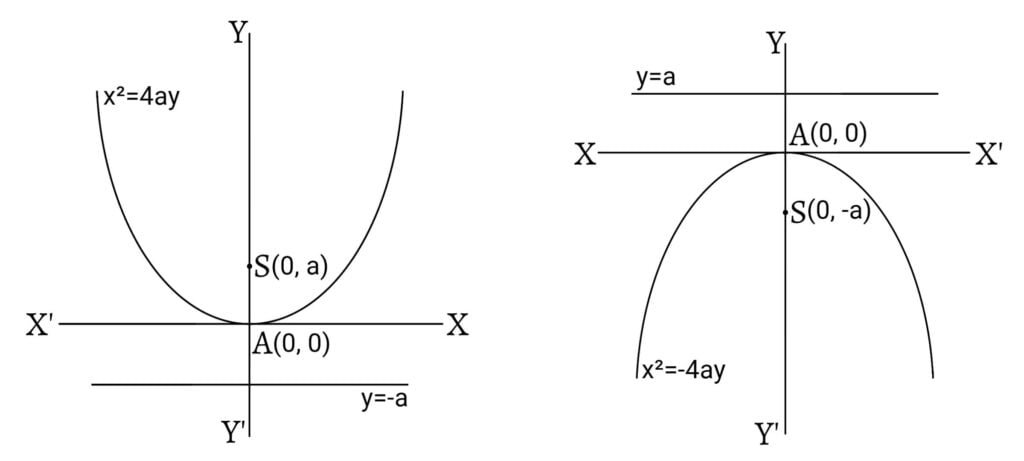
Similarly, if $a$ is positive, $x^2=4ay$ is a parabola whose axis is the y-axis, focus $(0,a)$ and directrix $\:y+a=0$ and the curve lies above the x-axis. If $a$ is negative, $x^2=-4ay$ lies below the x-axis.

Parameter

The point $(at^2,2at)$ clearly satisfies the equation of the parabola $y^2=4ax$. Here, $t$ is called the parameter. Hence, by the points $t_1$ and $t_2$ on the parabola, we mean the points $(at_1^2,2at_1)$ and $(at_2^2,2at_2)$.

Focal Distance, Focal Chord and Latus Rectum

Consider a parabola whose vertex is $A$ and focus is $S$. Let $P$ be any point on the parabola.

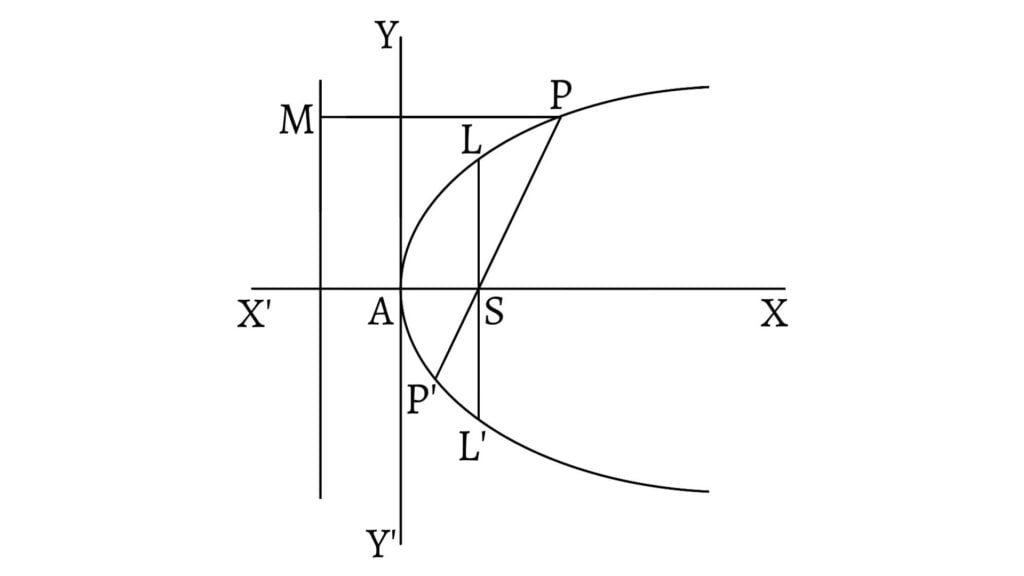
Focal Distance

The distance of any point on the parabola from the focus is called the focal distance or focal radius of the point. In the figure, $SP$ is the focal distance and $SP=PM=x+a$.

Focal Chord

Any chord of the parabola passing through the focus is called focal chord. In the figure, $PSP’$ is the focal chord of the parabola.

Latus Rectum

The chord of the parabola passing through the focus and perpendicular to the axis is called latus rectum. In the figure, $LSL’$ is the latus rectum. $L$ and $L’$ are the end points of the latus rectum which are the points of intersection of the parabola $y^2=4ax$ and the line $x=a$. By solving these two equations, we get $x=a$ and $y=\pm 2a$.

Hence, the coordinates of the end points $L$ and $L’$ of the latus rectum are $(a,2a)$ and $(a,-2a)$ respectively. \[\therefore LS=LS’=2a\]

Also, the length of the latus rectum is \[LL’=2a+2a=4a\]

Parabola with its Axis Parallel to the X-axis or Y-axis and Vertex at any Point

Let $(h,k)$ be the vertex of a parabola whose axis is parallel to the x-axis, so that its focus is at $(h+a,k)$, i.e. at a distance $a$ from the focus. The directrix is parallel to y-axis and at a distance $a$ from the vertex i.e. at a distance $(h-a)$ from the y-axis. Hence, equation of the directrix is \[x-h+a=0\]

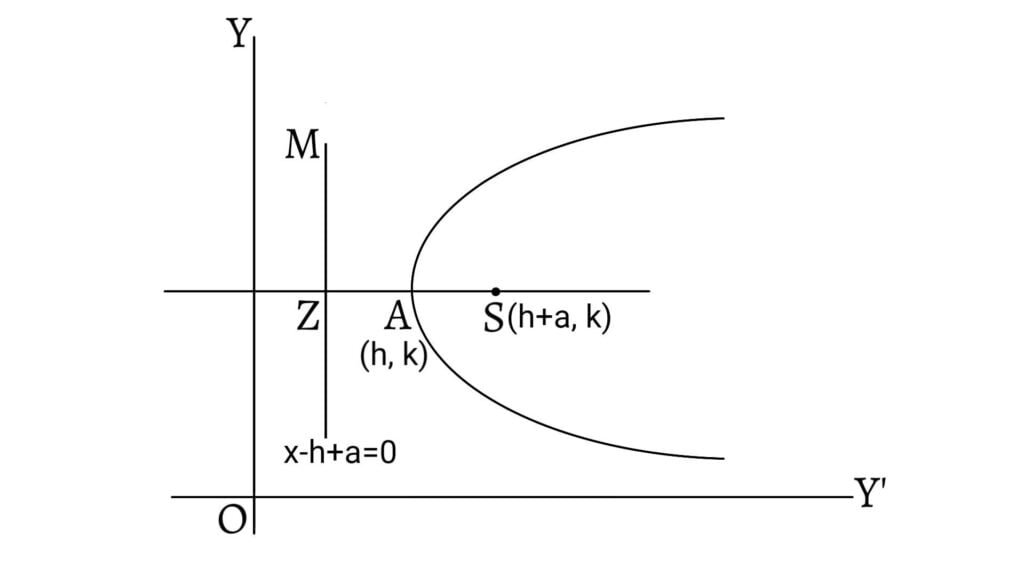
If $(x,y)$ be any point on the parabola, then its distance from the focus $(h+a,k)$ equals its distance from the directrix $x-h+a=0$. \[\therefore [x-(h+a)]^2+(y-k)^2=(x-h+a)^2\] \[\therefore (y-k)^2=4a(x-h)^2\]

This is the equation of the parabola.

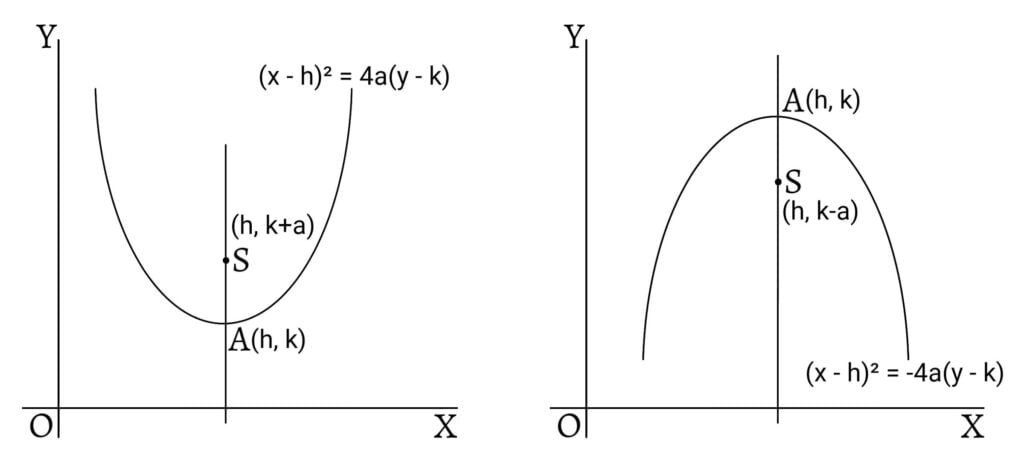
Similarly, the equation of a parabola with vertex at $(h,k)$ and axis parallel to the y-axis is \[(x-h)^2=4a(y-k)\]

Special Cases

If the y-coordinates of the vertex and the focus are same, then the axis of the parabola is parallel to x-axis. If the focus lies on the right of the vertex, then the parabola turns to the right and its equation is $(y-k)^2=4a(x-h)$. If the focus lies on the left of the vertex, then the parabola turns to the left and its equation is $(y-k)^2=-4a(x-h)$.

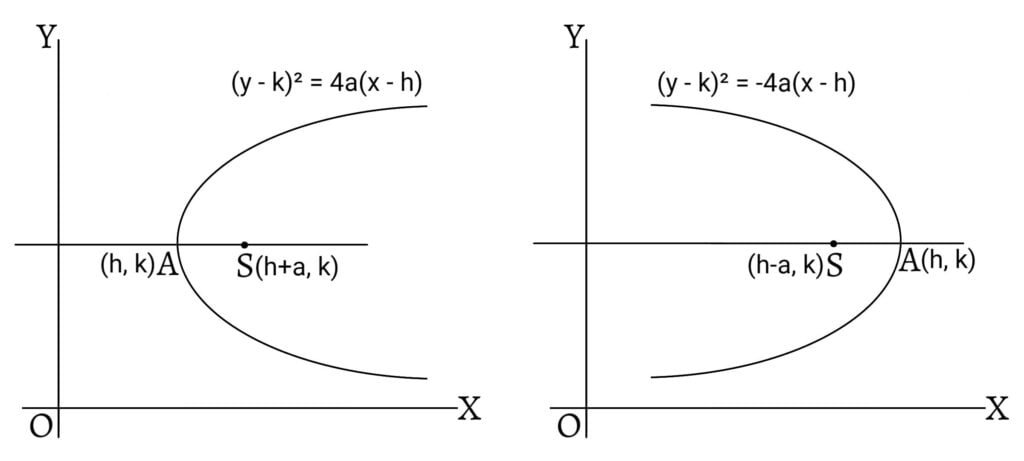
If the x-coordinates of the vertex and the focus are same, then the axis of the parabola is parallel to y-axis. If the focus lies above the vertex, then the parabola turns upward and its equation is $(x-h)^2=4a(y-k)$. If the focus lies below the vertex, then the parabola turns downward and its equation is $(x-h)^2=-4a(y-k)$.

General Equation of a Parabola

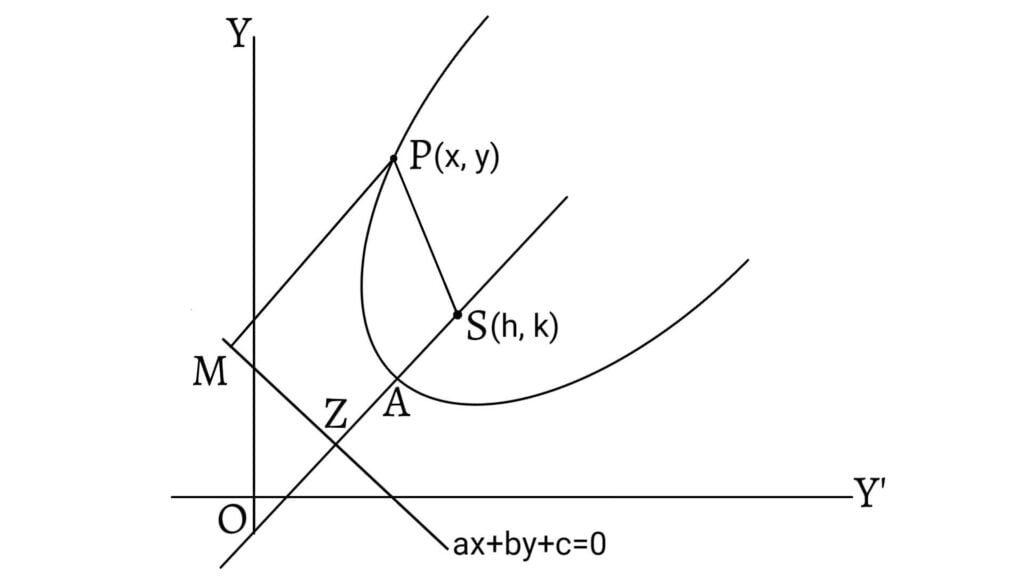
Let $(h,k)$ be the focus and $ax+by+c=0$ be the equation of the directrix of a parabola. Then if $(x,y)$ be any point on the parabola, its equation is \[(x-h)^2+(y-k)^2=\left(\frac{ax+by+c}{\sqrt{a^2+b^2}}\right)^2\]

By solving this equation, we get \[b^2x^2-2abxy+a^2y^2-2x\{(a^2+b^2)h+ac\}\]\[-2y\{(a^2+b^2)k+bc\}+(a^2+b^2)(h^2+k^2)-c^2=0\]

which is in the form of \[(bx-ay)^2+2gx+2fy+k=0\]

Thus, the characteristic property of the equation of a parabola is that the terms of the second degree form a perfect square.

---

---