Direction Cosines of a Line
Let a line $AB$ makes angles $\alpha$, $\beta$ and $\gamma$ with the direction x-axis, y-axis and z-axis respectively. Then, $\cos\alpha$, $\cos\beta$, $\cos\gamma$ are called the direction cosines (d.c.s) of the line $AB$. $\alpha$, $\beta$, $\gamma$ are called the direction angles. The direction cosines are generally denoted by $l$, $m$, $n$.

The direction cosines of the line $BA$ are $\cos(π-\alpha)$, $\cos(π-\beta)$ and $\cos(π-\gamma)$ as the direction angles of the line $OP’$ through $O$ parallel to $BA$ are $π-\alpha$, $π-\beta$ and $π-\gamma$. Hence, if $l$, $m$, $n$ are the direction cosines of the line $AB$, then $-l$, $-m$, $-n$ are the direction cosines of $BA$.
Direction Cosines of the Coordinate Axes
The x-axis makes angles $0$, $\frac{π}{2}$ and $\frac{π}{2}$ with x-axis, y-axis and z-axis respectively. Hence, the direction cosines of the x-axis are $\cos 0$, $\cos\frac{π}{2}$, $\cos\frac{π}{2}$ i.e. $1$, $0$, $0$. Similarly, the direction cosines of y-axis and z-axis are $0$, $1$, $0$ and $0$, $0$, $1$ respectively.
Theorem: $l^2+m^2+n^2=1$ where $l,m,n$ are the direction cosines of a line.
Let $AB$ be a line with direction cosines $l$, $m$, $n$. Consider a line $OP=r$ through the origin such that the angles made by $OP$ with coordinate axes are same as the angles made by $AB$ with coordinate axes. Let $OP$ makes angles $\alpha$, $\beta$, $\gamma$ with the coordinate axes so that $\cos\alpha$, $\cos\beta$, $\cos\gamma$ i.e. $l$, $m$, $n$ are the direction cosines of the line $AB$.
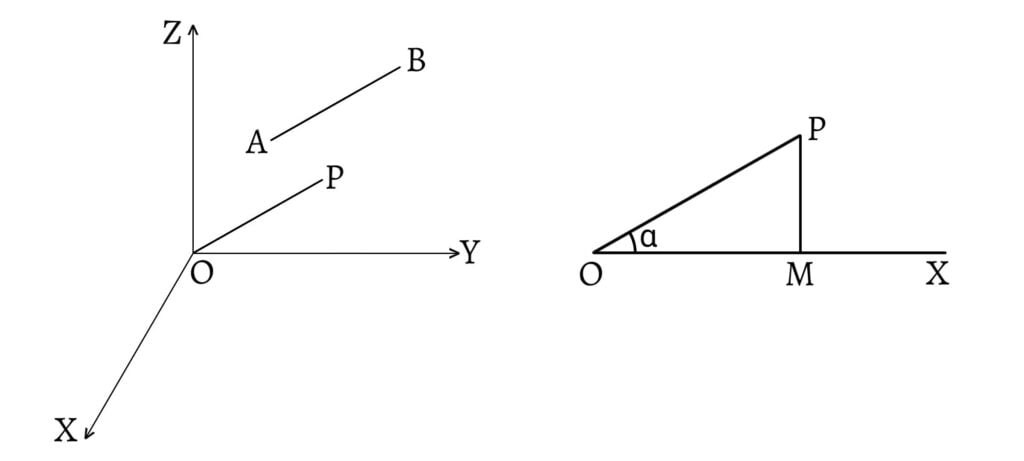
If $(x,y,z)$ be the coordinates of $P$ and $PM$ is drawn perpendicular to x-axis, then from the right angled $\Delta POM$, \[\cos\alpha=\frac{OM}{OP}\] \[\Rightarrow l=\frac{x}{r}\] \[\Rightarrow x=lr\] Similarly, \[y=mr\;\text{ and }\;z=nr\] Also, \[OP^2=x^2+y^2+z^2\] \[r^2=(lr)^2+(mr)^2+(nr)^2\] \[\therefore l^2+m^2+n^2=1\]
Direction Cosines of a Line through Two Given Points
Let a straight line $PQ$ $(=r)$ passing through the two given points $P(x_1,y_1,z_1)$ and $Q(x_2,y_2,z_2)$. Draw $PC\perp$ z-axis. From $C$, draw $CD$ equal and parallel to $PQ$ so that $CD$ and $PQ$ will be inclined to the z-axis at the same angle $\gamma$ (say). Now, draw $DC’\perp$ z-axis.

Then, we have \[n=\cos\gamma=\frac{CC’}{CD}\] \[\therefore n=\cos\gamma=\frac{z_2-z_1}{r}\]
Similarly, we can find that \[l=\cos\alpha=\frac{x_2-x_1}{r}\] \[m=\cos\beta=\frac{y_2-y_1}{r}\]
Hence, direction cosines of $PQ$ are \[\frac{x_2-x_1}{r},\frac{y_2-y_1}{r},\frac{z_2-z_1}{r}\] Also, \[\frac{x_2-x_1}{\cos\alpha}=\frac{y_2-y_1}{\cos\beta}=\frac{z_2-z_1}{\cos\gamma}=r\] where, \[r=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2}\]
[Learn about Direction Cosines in Vector: Direction Cosines of a Line]
Direction Ratios of a Line
If a set of three numbers $a$, $b$ and $c$ are proportional to the direction cosines $l$, $m$ and $n$ of a line, then they are called its direction ratios (d.r.’s). Since $a,b,c$ are proportional to $l,m,n$, we have \[\frac{l}{a}=\frac{m}{b}=\frac{n}{c}\] \[\frac{l}{a}=\frac{m}{b}=\frac{n}{c}=\frac{\sqrt{l^2+m^2+n^2}}{\sqrt{a^2+b^2+c^2}}=\frac{1}{\sqrt{a^2+b^2+c^2}}\]
Hence \[l=\frac{a}{\sqrt{a^2+b^2+c^2}}\] \[m=\frac{b}{\sqrt{a^2+b^2+c^2}}\] \[n=\frac{c}{\sqrt{a^2+b^2+c^2}}\]
Also, we know that the direction cosines of a line through two given points $(x_1,y_1,z_1)$ and $(x_2,y_2,z_2)$ are \[\frac{x_2-x_1}{r},\frac{y_2-y_1}{r},\frac{z_2-z_1}{r}\]
Here, the quantities $x_2-x_1$, $y_2-y_1$ and $z_2-z_1$ are the direction ratios of the given line.
