Consider two lines $AB$ and $CD$ with direction cosines $l_1$, $m_1$, $n_1$ and $l_2$, $m_2$, $n_2$. Let $OP_1$ $(=r_1)$ and $OP_2$ $(=r_2)$ be the lines through the origin $O$ parallel to the lines $AB$ and $CD$ so that the angle between them is equal to the angle between two lines $AB$ and $CD$. Let this angle be $\theta$.
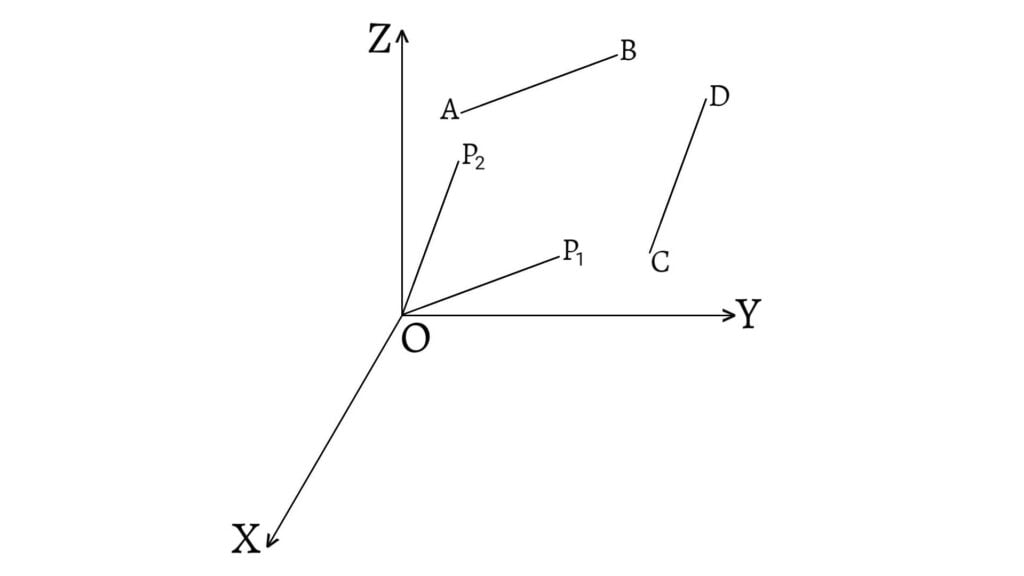
Then, the direction cosines of $OP_1$ and $OP_2$ are $l_1$, $m_1$, $n_1$ and $l_2$, $m_2$, $n_2$ respectively. Let the coordinates of $P_1$ and $P_2$ be $(x_1,y_1,z_1)$ and $(x_2,y_2,z_2)$ respectively. Now, the projection of $OP_2$ on $OP$ is $r_2\cos\theta$. The projection of $OP_2$ on $OP$ is also equal to $l_1x_2+m_1y_2+n_1z_2$.
\[\therefore r_2\cos\theta=l_1x_2+m_1y_2+n_1z_2\] \[\cos\theta=l_1\frac{x_2}{r_2}+m_1\frac{y_2}{r_2}+n_1\frac{z_2}{r_2}\] \[\therefore\cos\theta=l_1l_2+m_1m_2+n_1n_2\] This expression gives the angle $\theta$.
Expression for $\sin\theta$
We have, \[\sin^2\theta=1-\cos^2\theta\] \[=1-(l_1l_2+m_1m_2+n_1n_2)^2\] \[=(l_1^2+m_1^2+n_1^2)(l_2^2+m_2^2+n_2^2)-(l_1l_2+m_1m_2+n_1n_2)^2\] \[=(l_1m_2-l_2m_1)^2+(m_1n_2-m_2n_1)^2+(n_1l_2-n_2l_1)^2\]
Perpendicularity
If two lines are perpendicular to each other, then the angle between them is $\theta=90°$. \[\therefore \cos 90°=l_1l_2+m_1m_2+n_1n_2\] \[\therefore l_1l_2+m_1m_2+n_1n_2=0\] This is the condition for perpendicularity of two lines.
Parallelism
If two lines are parallel, then the angle between them $\theta=0°$. Hence, we have \[(l_1m_2-l_2m_1)^2+(m_1n_2-m_2n_1)^2+(n_1l_2-n_2l_1)^2=0\] This relation can be zero if each of the term in this relation is zero i.e. if \[\begin{array}{c}l_1m_2-l_2m_1=0,&m_1n_2-m_2n_1=0,&n_1l_2-n_2l_1=0\end{array}\] Therefore, we have, \[\frac{l_1}{l_2}=\frac{m_1}{m_2}=\frac{n_1}{n_2}\] \[\Rightarrow\frac{l_1}{l_2}=\frac{m_1}{m_2}=\frac{n_1}{n_2}=\frac{\sqrt{l_1^2+m_1^2+n_1^2}}{\sqrt{l_2^2+m_2^2+n_2^2}}=1\] \[\therefore l_1=l_2,m_1=m_2\;\text{and}\;n_1=n_2\] This is the required condition for parallelism of two lines.
Angle between two lines whose direction ratios are given
Let $a_1,b_1,c_1$ and $a_2,b_2,c_2$ be the direction ratios of two lines whose corresponding direction cosines are $l_1,m_1,n_1$ and $l_2,m_2,n_2$. Then, \[\begin{array}{c} l_1=\frac{a_1}{\sqrt{a_1^2+b_1^2+c_1^2}},&m_1=\frac{b_1}{\sqrt{a_1^2+b_1^2+c_1^2}},&n_1=\frac{c_1}{\sqrt{a_1^2+b_1^2+c_1^2}}\\l_2=\frac{a_2}{\sqrt{a_2^2+b_2^2+c_2^2}},&m_2=\frac{b_2}{\sqrt{a_2^2+b_2^2+c_2^2}},&n_2=\frac{c_2}{\sqrt{a_2^2+b_2^2+c_2^2}}\end{array}\]
If $\theta$ be the angle between the two lines, then we have \[\cos\theta=l_1l_2+m_1m_2+n_1n_2\] Putting the values of $l_1,m_1,n_1$ and $l_2,m_2,n_2$ and solving, we get \[\cos\theta=\frac{a_1a_2+b_1b_2+c_1c_2}{\sqrt{a_1^2+b_1^2+c_1^2}\sqrt{a_2^2+b_2^2+c_2^2}}\]
Perpendicularity
If two lines are perpendicular to each other, then $\theta=90°$. \[\therefore a_1a_2+b_1b_2+c_1c_2=0\] This is the required condition for perpendicularity of two lines.
Parallelism
If two lines are parallel, then $\theta=0°$. \[\therefore 1=\frac{(a_1a_2+b_1b_2+c_1c_2)^2}{(a_1^2+b_1^2+c_1^2)(a_2^2+b_2^2+c_2^2)}\] \[(a_1^2+b_1^2+c_1^2)(a_2^2+b_2^2+c_2^2)-(a_1a_2+b_1b_2+c_1c_2)^2=0\] \[(a_1b_2-a_2b_1)^2+(b_1c_2-b_2c_1)^2+(c_1a_2-c_2a_1)^2=0\]
This relation is true only if each of the term in this relation is zero i.e. if \[\begin{array}{c}a_1b_2-a_2b_1=0,&b_1c_2-b_2c_1=0,&c_1a_2-c_2a_1=0\end{array}\] Therefore, we have \[\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\] This is the required condition for parallelism of two lines.
Previous: Direction Cosines and Direction Ratios of a Line
