Reimann Sum generalises the idea developed in the last section: Area as a Definite Integral. For this, the function, we consider, must be continuous. Consider a function $ƒ$ defined and continuous in an interval $[a,b]$. Consider a finite set of points $x_0,x_1,…,x_n$ such that \[a=x_0<x_1<…<x_{n-1}<x_n=b\] This set of points is called a partition of the interval $[a,b]$. This set divides the interval $[a,b]$ into $n$ subintervals whose lengths be \[\Delta x_i=x_i-x_{i-1}\text{ } [i=1,2,3,…,n]\] The greatest length of these subintervals is called the norm or mesh of the partition i.e. $\text{mesh}=\text{max. }\Delta x_i$.
Take any point $t_i$ in the interval $[x_{i-1},x_i]$, then the sum \[\sum_{i=1}^n ƒ(t_i)\Delta x_i\] is called a Reimann Sum for the function in the interval $[a,b]$. Now as $n\to\infty$, $\Delta x_i\to0$. In this case, as we know from Area as a Definite Integral, the Reimann sum tends to a limit which is equal to the area under the curve of the continuous function $ƒ$.
If the Reimann sum $\sum_{i=1}^nƒ(t_i)\Delta x_i$ tends to a limit $I$, as the mesh approaches zero for every choice of the point $t_i$ in $[x_{i-1},x_i]$, then $I$ is called the definite integral of $ƒ$ from $a$ to $b$. \[I=\int_a^bƒ(x)dx=\lim_{\text{mesh}\to 0}\sum ƒ(t_i)\Delta x_i\] Here, $a$ is called the lower limit and $b$ is called the upper limit of the integral.
The existence of definite integral for some functions is guaranteed by the theorem “If $ƒ$ is continuous in the interval $(a,b)$ then $\int_a^bƒ(x)dx$ exists“.
If $ƒ(x)$ is continuous on $[a,b]$, then the area bounded by the curve $y=ƒ(x)$, the x-axis and the two ordinates $x=a$, $x=b$ is equal to $\int_a^bydx$.
The curve represented by $y=ƒ(x)$ is shown in the figure given below. Let $A$ and $B$ be two points on the curve with the ordinates $AC$ at $x=a$ and $BD$ at $x=b$. Let $P(x,y)$ and $Q(x+\Delta x,y+\Delta y)$ be two neighbouring points on the curve. Complete the rectangles $PMNR$ and $SMNQ$.

Let $A(x)$ be the area of the figure $ACMP$ which is equal to the area bounded by the curve $y=ƒ(x)$, x-axis, the fixed ordinate $AC$ and the variable ordinate $PM$. As $x$ increases, $A(x)$ increases. So, if $x$ is increased to $x+\Delta x$, then $A(x+\Delta x)$=area of $ACNQ$. \[\therefore A(x+\Delta x)-A(x)=\text{Area of }PMNQ\] From the figure, \[\text{Rect. }PMNR<\text{Area of }PMNQ<\text{Rect. }SMNQ\] \[\Rightarrow y\Delta x<A(x+\Delta x)-A(x)<(y+\Delta y)\Delta x\] \[\Rightarrow y<\frac{A(x+\Delta x)-A(x)}{\Delta x}<y+\Delta y\] \[\Rightarrow \lim_{\Delta x\to 0}y<\lim_{\Delta x\to 0}\frac{A(x+\Delta x)-A(x)}{\Delta x}<\lim_{\Delta x\to 0}(y+\Delta y)\] \[\Rightarrow y<A'(x)<\lim_{\Delta x\to 0}(y+\Delta y)\] \[\text{Since, }\lim_{\Delta x\to 0}(y+\Delta y)=\lim_{\Delta y\to 0}(y+\Delta y)=y\] \[\therefore A'(x)=y=ƒ(x)\] Hence, $A(x)$ is the antiderivative of $ƒ(x)$.
Now using the fundamental theorem of integral calculus, we have \[\int_a^bƒ(x)dx=A(b)-A(a)\] \[\Rightarrow\int_a^bƒ(x)dx=A(x)\text{ at }x=a-A(x)\text{ at }x=b\] \[=\text{Area of }ACDB-0\] \[\therefore \int_a^bydx=\text{Area of }ACDB\] which is the area bounded by the curve $y=ƒ(x)$, x-axis and the two ordinates $x=a$ and $x=b$. In this proof, we have assumed that $ƒ(x)≥0$ (i.e. the curve lies above the x-axis). Now we discuss this for different cases given below.
Cor. 1: If the curve $y=ƒ(x)$ lies below the x-axis (i.e. $ƒ(x)≤0$) then the area bounded by the curve $y=ƒ(x)$, x-axis and the two ordinates $x=a$ and $x=b$ is given by \[\int_a^b(-y)dx=-\int_a^bƒ(x)dx\]

Cor. 2: If the curve $x=ƒ(y)$ lies on the right of y-axis (i.e. $ƒ(y)≥0$) then the area bounded by the curve $x=ƒ(y)$, y-axis and the two abscissae $y=a$ and $y=b$ is given by \[\int_a^b xdy=\int_a^bƒ(y)dy\]

Cor. 3: If the curve $x=ƒ(y)$ lies on the left of y-axis (i.e. $ƒ(y)≤0$) then the area bounded by the curve $x=ƒ(y)$, y-axis and the two abscissae $y=a$ and $y=b$ is given by \[\int_a^b(-x)dy=-\int_a^bƒ(y)dy\]

If the required area be negative, we consider the positive value because we need only the magnitude of the area.
Find the area bounded by the x-axis, the curve $y=4x^3$ and ordinates $x=2$ and $x=4$.

\[\text{Area }(A)=\int_2^4ydx=\int_2^44x^3dx\]\[=4\left[\frac{x^4}{4}\right]_2^4=4^4-2^4=240\text{ sq. units}\]
Find the area bounded by y-axis, the curve $x^2=4a(y-2a)$ and $y=6a$.
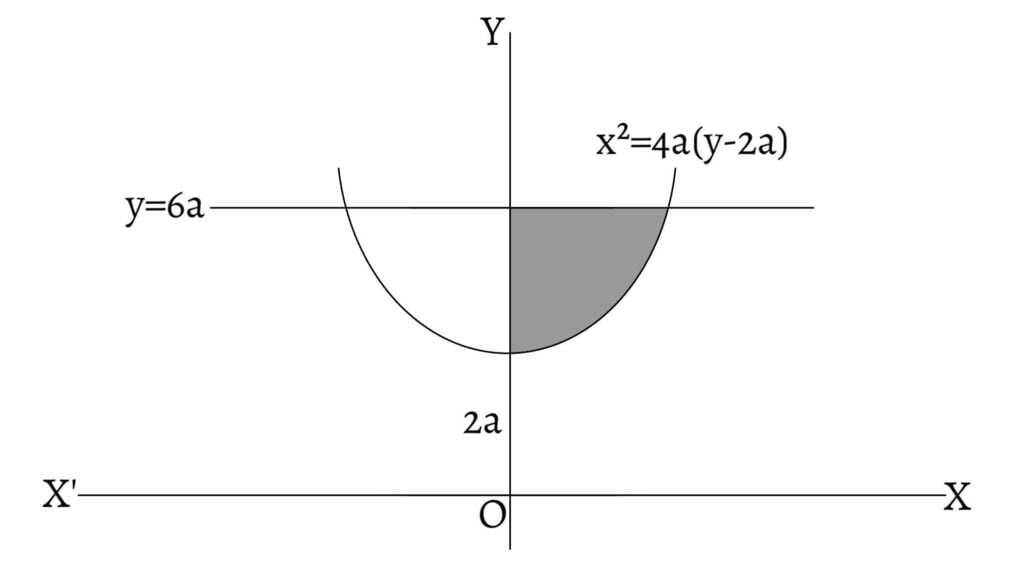
Put $x=0$, then, \[0=4a(y-2a)\] \[\therefore y=2a\] \[\therefore \text{Area }(A)=\int_{2a}^{6a}xdy=\int_{2a}^{6a}\sqrt{4a(y-2a)}dy\] \[=2\sqrt{a}\int_{2a}^{6a}(y-2a)^{\frac{1}{2}}dy=\frac{4\sqrt{a}}{3}\left[(y-2a)^{\frac{3}{2}}\right]_{2a}^{6a}\] \[=\frac{4\sqrt{a}}{3}\left[(4a)^{\frac{3}{2}}-0\right]\] \[=\frac{4\sqrt{a}}{3}(4a).2\sqrt{a}=\frac{32}a^2{3}\text{ sq. units}\]
Area between Two Curves

Now Let us find out the area enclosed by the curves represented by two given functions $ƒ_1$ and $ƒ_2$ and the given ordinates $x=a$ and $x=b$. Let $PQ$ be the curve given by the function $ƒ_1$ and $SR$ be the curve given by the function $ƒ_2$. Let $PSA$ and $QRB$ be the ordinates given by $x=a$ and $x=b$ respectively. Now \[\text{Area of }PQRS=\int_a^bƒ_1(x)dx-\int_a^bƒ_2(x)dx\] \[=\int_a^b(y_1-y_2)dx\]
Find the area of the region between $y^2=4ax$ and $x^2=4ay$.

Eliminating $y$ between above equations, \[\left(\frac{x^2}{4a}\right)^2=4ax\] \[x^4=64a^3x\] \[x(x^3-64a^3)=0\] \[\therefore x=0,4a\] \[\therefore \text{Area }(A)=\int_0^{4a}(y_1-y_2)dx\] \[=\int_0^{4a}y_1dx-\int_0^{4a}y_2dx\] \[=\int_0^{4a}\sqrt{4ax}\text{ }dx-\int_0^{4a}\frac{x^2}{4a}dx\] \[=\frac{4\sqrt{a}}{3}\left[x^{\frac{3}{2}}\right]_0^{4a}-\frac{1}{12a}\left[x^3\right]_0^{4a}\] \[=\frac{4\sqrt{a}}{3}(4a)^{\frac{3}{2}}-\frac{1}{12a}(64a^3)=\frac{16}{3}a^2\text{ sq. units}\]
Previous: Area as a Definite Integral
Explore Antiderivatives
- Antiderivative (Indefinite Integral)
- Antiderivatives by Substitution Method
- Integration by Parts
- Definite Integral
- Standard Integrals (I)
- Standard Integrals (II)
- Standard Integrals (III)
- Integration of Rational Fractions
