Function | Relations And Functions

Relation is a very broad concept. It has various forms in a very natural way. To make it more useful and concrete, it is necessary to refine it. Let’s begin with a relation $ℜ$ on a set $A$ and an ordered pair $(a, b) ∈ ℜ$. A refinement of $ℜ$ can be obtained by assigning only one second element $b$ to each first element $a$ of the pair $(a, b)$. Such a refinement of a relation is known as function.

Variable and Constant

Consider a function defined from set $A$ to another set $B$ or the same set $A$. If $x∈A$, i.e., $A=\{x:x\;\text{satisfies a certain property}\}$, the letter or symbol, $x$ is known as a variable. Each number or element of the set $A$ is called the value of the variable $x$. If $x∈A=\{1, 2, 3\}$, then $x$ is a variable which stands for one of the members $1$, $2$, $3$. Here, each of the numbers $1$, $2$, $3$ is a value of the variable $x$.

Consider a singleton set $C=\{c\}$ i.e. a set $C$ consisting of only one member $c$, then the letter or symbol $c$ is known as a constant. In other words, a constant has a fixed value.

Consider two sets $A$ and $B$. Then, any non-empty subset $ℜ$ of the Cartesian product $A×B$ is known as a relation from $A$ to $B$. Refinement of this relation can be done by associating each element of the set $A$ with a unique element of $B$.

Example 1:

Let $A=\{1, 2, 3\}$ and $B=\{2, 4, 6\}$.

$A×B=\{(1, 2), (1, 4), (1, 6), (2, 2), (2, 4), (2, 6),$$(3, 2), (3, 4), (3, 6)\}$

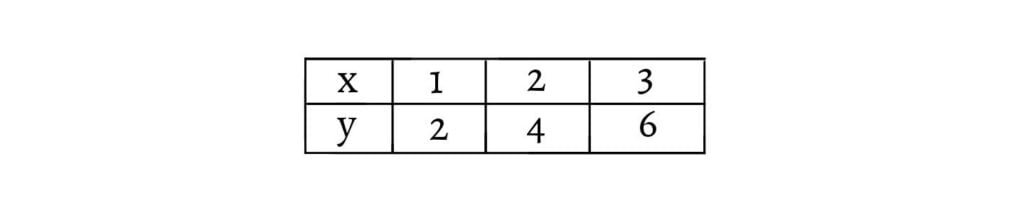
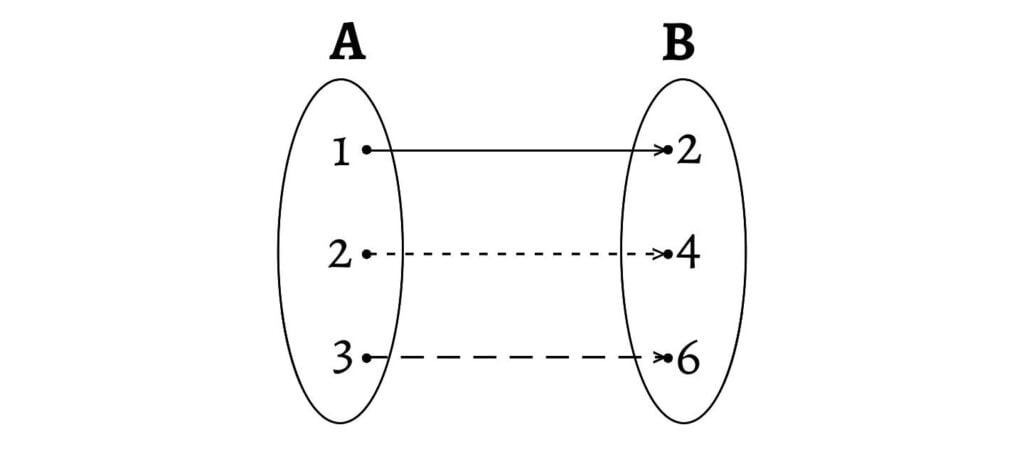
Let us make the following selection (or refinement): $\{(1, 2), (2, 4), (3, 6)\}$. This is a refined relation from $A$ to $B$. Here, each first element is uniquely associated with a second element. The rule or relation corresponding to the present assignment is, “To each first element, there corresponds a unique second element that is twice the first element“.

In tabular form:

Graphically,

In arrow diagram:

Example 2:

Let $A=\{a, b, c, d\}$ and $B=\{x, y, z, t\}$.

$A×B=\{(a, x), (a, y), (a, z), (a, t), (b, x), (b, y),$$(b, z), (b, t), (c, x), (c, y), (c, z), (c, t),(d, x), (d, y),$$ (d, z), (d, t)\}$

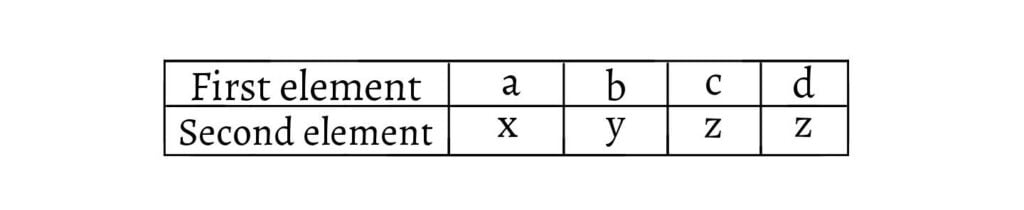
Let us make the following selection: $\{(a, x), (b, y), (c, z), (d, z)\}$. This is a refined relation from $A$ to $B$. Here, each first element is uniquely associated with a second element. But there is a slight difference, there are two first elements that correspond to one second element.

In tabular form:

In arrow diagaram:

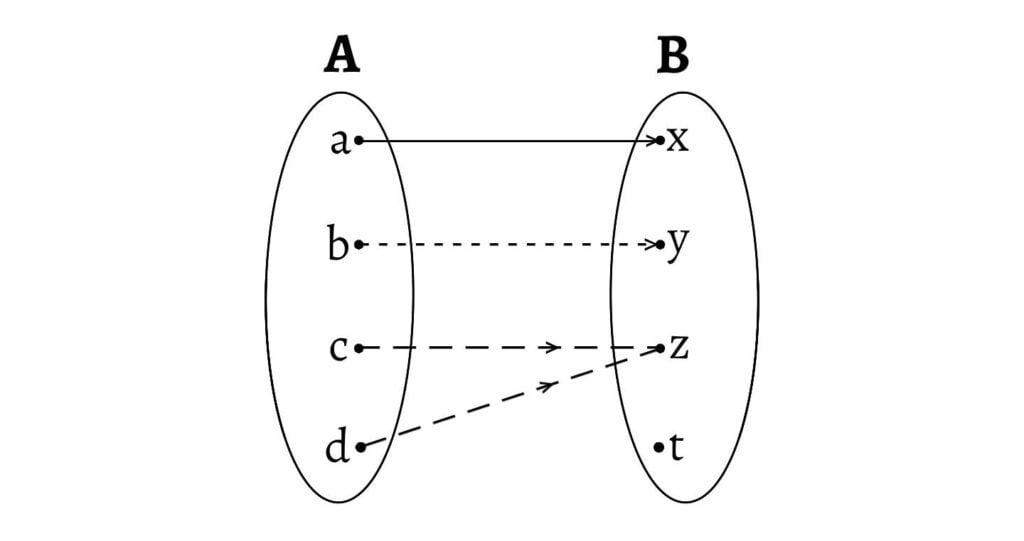
Although every first element is associated with a unique second element, there is one element of the second set $B$ that is not associated with any element of $A$.

A relation is said to be a function from set $A$ to set $B$ if every element of set $A$ associates with a unique element of set $B$.

In other words, a function from a set $A$ to a set $B$ is a relation $ƒ$ such that for each $a∈A$, $∃$ a unique $b∈B$ s.t. $(a, b)∈ƒ$.

Here, “$∃$” is read “there exists” and “s.t.” stands for “such that”.

Also, a function from a set $A$ to a set $B$ is a relation in which no two ordered pairs have the same first co-ordinate.

A function $ƒ$ from a set $A$ to a set $B$ is denoted by, \[ƒ:A \to B\] \[\text{or, } A \xrightarrow{ƒ} B\]

Image, Pre-image, Domain and Range of a Function

If $y∈B$ is associated with an element $x∈A$, we write it as, \[y=ƒ(x)\] which is read “$y$ equals $f$ of $x$”. $ƒ(x)$ is known as the image of $ƒ$ at $x$ or value of $ƒ$ at $x$.

If $b$ is the unique element of $B$ corresponding to an element $a$ of $A$ under the function $ƒ$, then $a$ is called the pre-image of $b$ under $ƒ$ and $b$ is called the image of a under $ƒ$. \[b=ƒ(a)\] The element $y∈B$ with which the element $x∈A$ associates, is known as the image of $x$ under $ƒ$. The element $x∈A$ which associates with $y∈B$, is known as the pre-image of $y$ under $ƒ$.

It is to be noted that if $ƒ$ is a function from $A$ to $B$, then no element of $A$ is related to more than one element of $B$; although more than one element of $A$ can be related to the same element of $B$. In each case, $A$ is called the domain of $ƒ$ and $B$ its co-domain.

The subset of $B$ that contains only those elements of $B$ that have pre-images in $A$ is called the range of $ƒ$. \[\text{Range of }ƒ⊆B\] Therefore, in a function $ƒ: A\to B$, the set of values of $x∈A$ for which the function is defined, is said to be the domain of the function. It is denoted by $\text{dom}(ƒ)$ or simply $D(ƒ)$.

\[∴ D(ƒ) = \{x:x∈A\;\text{for which}\; ƒ(x)\; \text{is defined}\}\]

The set of values of $y=ƒ(x)∈B$ for every $x∈A$ is known as the range of the function. It is denoted by $\text{range}(ƒ)$ or simply $R(ƒ)$.

\[∴ R(ƒ) = \{y:y∈B, y=ƒ(x)\;\text{for all}\;x∈A\}\]

Example 3:

\[y=ƒ(x)=\sqrt{x-1}\] then, $ƒ(x)$ is defined for $x-1≥0$ i.e. $x≥1$. Thus, \[D(ƒ)=\{x:x≥1\}=[1,\infty)\] \[R(ƒ)=\{y:y≥0\}=[0,\infty)\]

In the function $ƒ:A\to B$, $A$ itself is the domain of $ƒ$ and the set of values of $y∈B$ which are the images of the elements of $A$, is the range of $ƒ$.

A function is also called a mapping. In some special context, a transformation or an operator.

Since $y$ is the image of an element $x$ under a function $ƒ$, $ƒ$ is also indicated by \[x \mapsto y \text{ or, } x \mapsto ƒ(x)\]

In the above example: 2 where $A=\{a, b, c, d\}$ and $B=\{x, y, z, t\}$ and the refinement, $\{(a,x),(b,y),(c,z),(d,z)\}$.

The function $ƒ:A\to B$ may be described by equations \[ƒ(a)=x,ƒ(b)=y,ƒ(c)=z \text{ and } ƒ(d)=z\] \[\therefore D(ƒ)=\{a,b,c,d\}\] \[R(ƒ)=\{x,y,z\}\] Here, \[ƒ(A)≠B \text{ and } ƒ(c)=ƒ(d)=z\]

If two functions $ƒ$ and $g: A\to B$ have a same domain $D$, then they are said to be equal iff $ƒ(x)=g(x)$ for every $x∈A⊆D$; and is written as $ƒ=g$.

More on Relations And Functions