Types of Functions | Relations And Functions

There are three types of functions;

One-one or Injective function
Onto or Surjective function
One-one onto or Bijective function

One-one or Injective Function

A function $ƒ: A\to B$ is said to be one-one or injective, if distinct elements (or pre-images) in $A$ have distinct images in $B$.

For any $x, y ∈ A$, \[x ≠ y \Rightarrow ƒ(x) ≠ ƒ(y); \] or, equivalently, \[ƒ(x)=ƒ(y) \Rightarrow x=y\] In other words, a function $ƒ$ is said to be one-one or injective if \[(x, ƒ(x)), (y, ƒ(y)) ∈ ƒ \Rightarrow x=y\] Thus, under one-one function all elements of $A$ are related to different elements of $B$.

Examples:

The function $ƒ: Z\to Z$ ($Z$ is a set of integers) defined by $ƒ(x)=2x$ is one-one, since \[ƒ(x)=ƒ(y) \Rightarrow 2x=2y \Rightarrow x=y\] It can be diagrammatically represented by

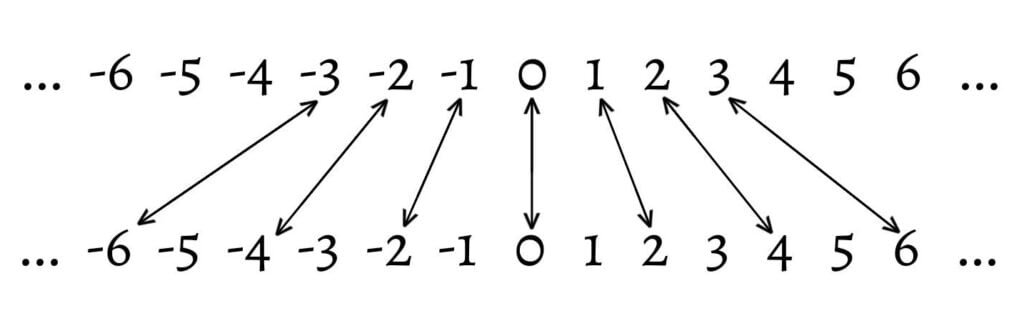
One-one or Injective Function: One-one and into (Types of Functions)

Here, $ƒ(Z)=\{…, -4, -2, 0, 2, 4, …\}⊂Z$. In such a case, the function is said to be one-one and into.

A function $ƒ: A\to B$ is said to be into function if at least one element of $B$ has no pre-images in $A$.

2. The function $ƒ: R\to R$ ($R$ is the set of real numbers) defined by $ƒ(x)=x^3$ is one-one, since the cubes of different real numbers are themselves different.

3. The function $ƒ: N\to R$ ($N$ is the set of natural numbers) defined by $ƒ(x)=x^2$, is one-one and into, since the squares of different natural numbers are themselves different and $ƒ(N)⊂R$.

4. The function $ƒ: R\to R$ defined by $ƒ(x)=x^2$, is not one-one, since $ƒ(2)=ƒ(-2)=4$, i.e. the images of two numbers $-2$ and $2$ have a same image $4$.

Onto or Surjective Function

A function $ƒ: A\to B$ is said to be onto or surjective function, if every element of $B$ is an image of at least one element of $A$ i.e. every element of $B$ has a pre-image. Then, \[ƒ(A)=B\]

Examples:

Let $A=\{-3, -2, -1, 1, 2, 3\}$ and $B=\{1, 4, 9\}$. Then, $ƒ: A\to B$ defined by $ƒ(x)=x^2$ is onto.

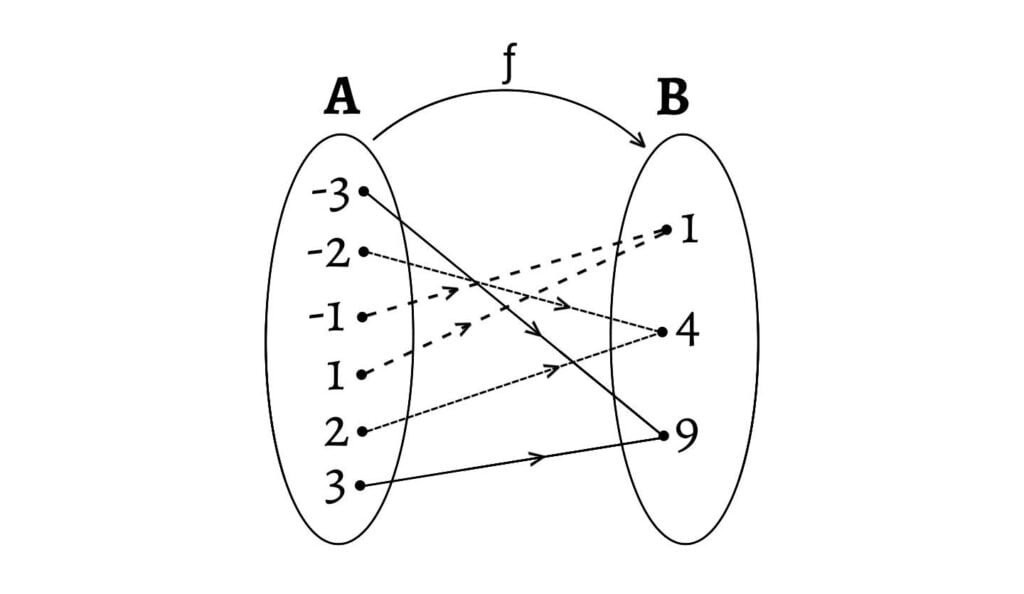
Onto or Surjective Function: Arrow diagram, many-one onto fuction

Here, $ƒ(A)=B$. This function is many-one onto.

A function $ƒ: A\to B$ is said to be many-one if two or more elements of set $A$ have a same image in set $B$.

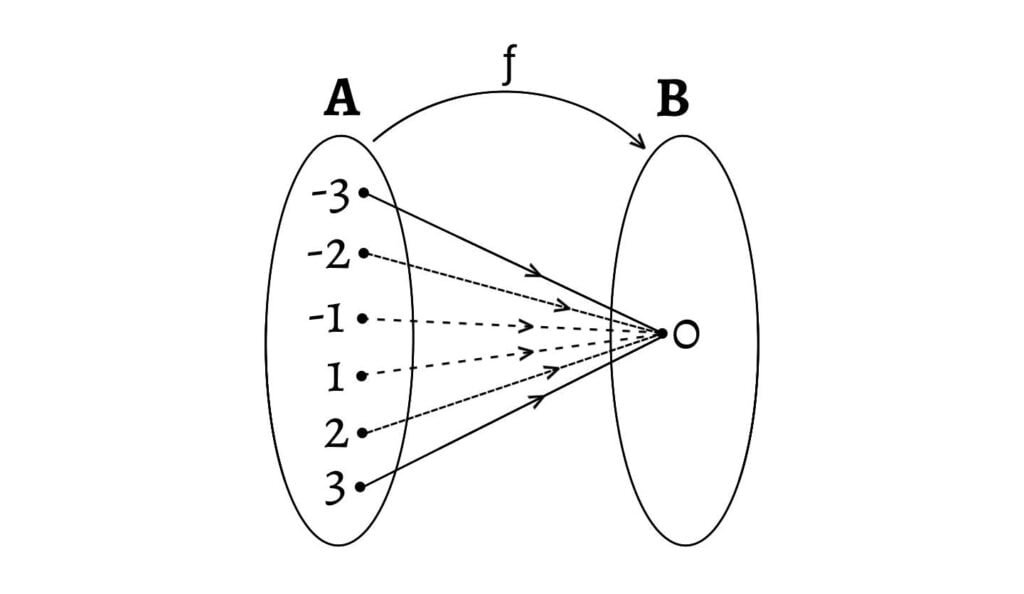
2. A function $ƒ: A\to B$ such that $ƒ(x)=c ∈ B$ for every $x ∈ A$ is a many-one onto function. Such a function is called a constant function. \[ƒ:A=\{-3,-2,-1,1,2,3\}\rightarrow B=\{0\}\]

Onto or Surjective Function: Arrow diagram, constant function

3. Let $A=\{a, b, c\}$ and $B=\{1, 2\}$, then,

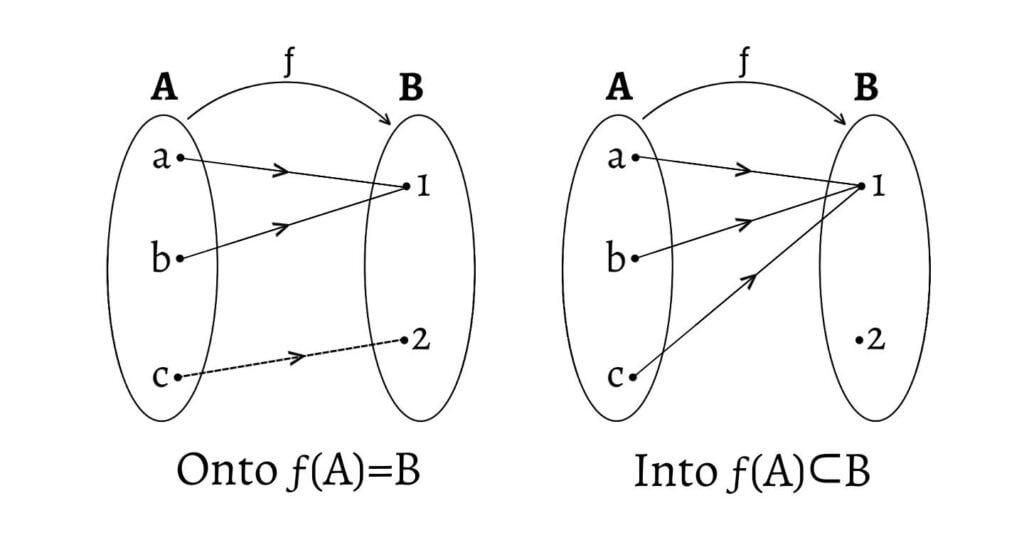
4. The function $ƒ: Z\to N$, where $Z$ is the set of integers and $N$ is the set of natural numbers, defined by $ƒ(x)=x^2$ is not onto, since there is no $x∈Z$ s.t. $ƒ(x)=x^2=2$. There are several pairs of values of $x$ which has the same image. $ƒ(Z)≠N$ but $ƒ(Z)⊂N$. Hence, this is a many-one into function.

One-one Onto or Bijective Function

A function that is both one-one and onto (i.e. injective and surjective) is called a bijective function. It is also known as a one-to-one correspondence.

A bijective function from a set $A$ to itself $ƒ: A\to A$ is known as a permutation or operator on $A$.

Examples:

Let $A=\text{{Earth, Jupiter, Saturn}}$ and $B=\text{{Moon, Io, Titan}}$. Then, the following diagram shows a bijective function.

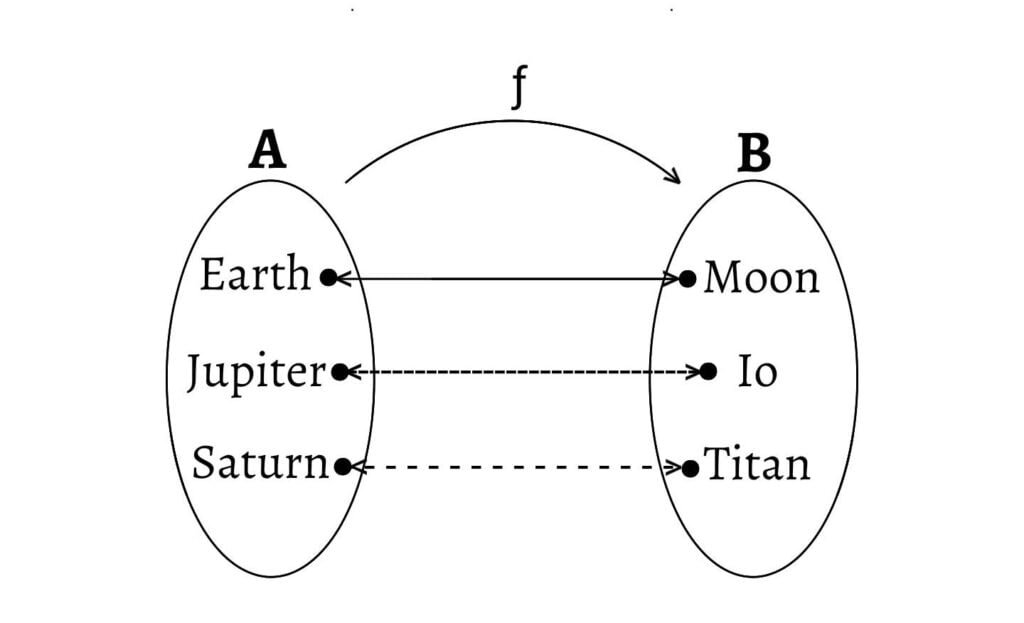
2. The function $ƒ: A\to B$ defined by $ƒ(x)=x$ for all $x∈A$ is a bijective function. This function is also known as an identity function.

3. The function $ƒ: N\to \{3\}$ defined by $ƒ(x)=3$ for all $x∈N$ is not one-one but onto. So, it is not a bijective function.

More on Relations And Functions