A complex number $z$ is defined as an ordered pair $(x,y)$ of real numbers. In the Cartesian plane, every ordered pair of real numbers can be represented by a point. Hence, the complex number $z=(x,y)$ can be represented with a point $P$ in the Cartesian plane with coordinates $(x,y)$. Thus, every point in the plane represents a complex number and is called the complex plane.
When complex numbers are represented by points in the Cartesian plane, the plane is called the complex plane; and the set of such points form an Argand diagram. The idea of expressing complex numbers geometrically was formulated by Argand (French) and Gauss (German). The name “complex number” is due to Gauss.

Let $z=(x,y)=x+iy$ be a complex number represented by a point $P$ in the complex plane. Then, the modulus of the complex number $z$ is given by \[|z|=\sqrt{x^2+y^2}=OP\]
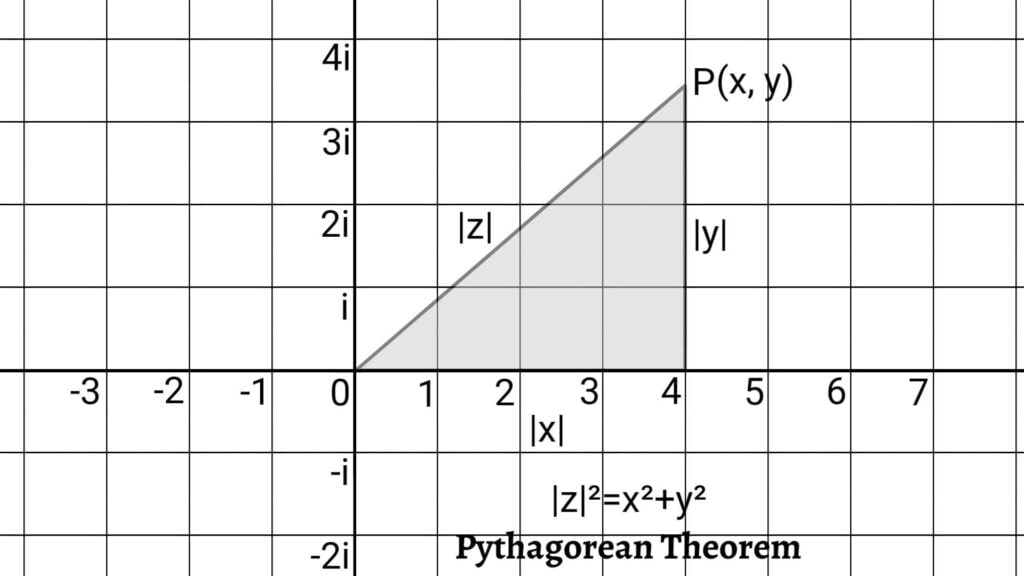
In other words, the modulus of a complex number is the distance of the point representing the complex number from the origin in the complex plane.
The Unit Circle
The unit circle is the set of all points in the complex numbers with absolute value $1$. We know that $1$ is the absolute value of both $1$ and $-1$. It is also the absolute value of $i$ and $-i$ since they are both one unit away from $0$ on the imaginary axis.

Hence, the unit circle is the circle of radius $1$ centered at $0$. It includes all complex numbers of absolute value $1$, so the equation of unit circle is $|z|=1$.
Previous: The Cube Roots of Unity
