Parallel Forces

Forces are said to be parallel forces, if they act along parallel lines.

Two parallel forces are said to be like when they act in the same direction and they are said to be unlike when they act in opposite directions. And, there exists a single force whose effect is the same as that of the two parallel forces.

Resultant of two like parallel forces

Let two like parallel forces $P$ and $Q$ acting at points $A$ and $B$ respectively on a rigid body be represented by the lines $A{L}_1$ and $B{L}_2$. Join $AB$.

Apply two equal and opposite forces, each being equal to $S$ along $BA$ and $AB$ represented by $A{M}_1$ and $B{M}_2$ respectively. These two forces balance each other and have no impact upon the equilibrium of the body [Forces in Equilibrium]. Complete the parallelograms $A{L}_1{N}_1{M}_1$ and $B{L}_2{N}_2{M}_2$. Let the diagonals $N_{1}A$ and $N_{2}B$ be produced to meet at $O$. Through $O$, draw $OC$ parallel to $A{L}_1$ or $B{L}_2$ to meet $AB$ in $C$.

Now, the forces $P$ and $S$ at $A$ have a resultant $R_1$ represented by $A{N}_1$ and let its point of application be transferred to $O$. Similarly, the forces $Q$ and $S$ at $B$ have the resultant $R_2$ represented by $B{N}_2$ and let its point of application be transferred to $O$.

The force $R_1$ at $O$ can be resolved into two components; $S$ parallel to $A{M}_1$ and $P$ in the direction $OC$. Similarly, the force $R_2$ at $O$ may be resolved into two components; $S$ parallel to $B{M}_2$ and $Q$ in the direction $OC$. [Resolution of Forces]

Hence, the given forces are equivalent to two forces $P$ and $Q$ along $OC$ and two forces each equal to $S$ acting in opposite directions. The first two forces are equivalent to a single force $(P+Q)$ along $OC$ and the forces equal to $S$ balance one another. Thus, the resultant of two like parallel forces $P$ and $Q$ is equivalent to a force $(P+Q)$ along $OC$.

The point of application of the resultant

Since the $\mathrm{\Delta }OCA$ and $\mathrm{\Delta }A{L}_1{N}_1$ are similar, $$\frac{OC}{=}\frac{CA}{L_1{N}_1}$$ $$\frac{OC}{P}=\frac{CA}{A{M}_1}$$ $$\frac{OC}{P}=\frac{CA}{S}$$ $$S\times OC=P\times CA\text{ \_\_(1)}$$ Again, the $\mathrm{\Delta }OCB$ and $\mathrm{\Delta }B{L}_2{N}_2$ are similar, $$\frac{OC}{B{L}_2}=\frac{CB}{L_2{N}_2}$$ $$\frac{OC}{Q}=\frac{CB}{S}$$ $$S\times OC=Q\times CB\text{ \_\_(2)}$$ From $\text{(1)}$ and $\text{(2)}$, $$P\times CA=Q\times CB$$ $$\frac{CA}{CB}=\frac{Q}{P}$$ i.e. $C$ divides the line $AB$ internally in the inverse ratio of the force.

Cor.1. $$\frac{P}{CB}=\frac{Q}{CA}=\frac{P+Q}{CB+CA}=\frac{R}{AB}$$

Resultant of two unlike parallel forces

Let two unlike parallel forces $P$ and $Q$ such that $P>Q$ acting at points $A$ and $B$ respectively on a rigid body be represented by the lines $A{L}_1$ and $B{L}_2$. Join $AB$.

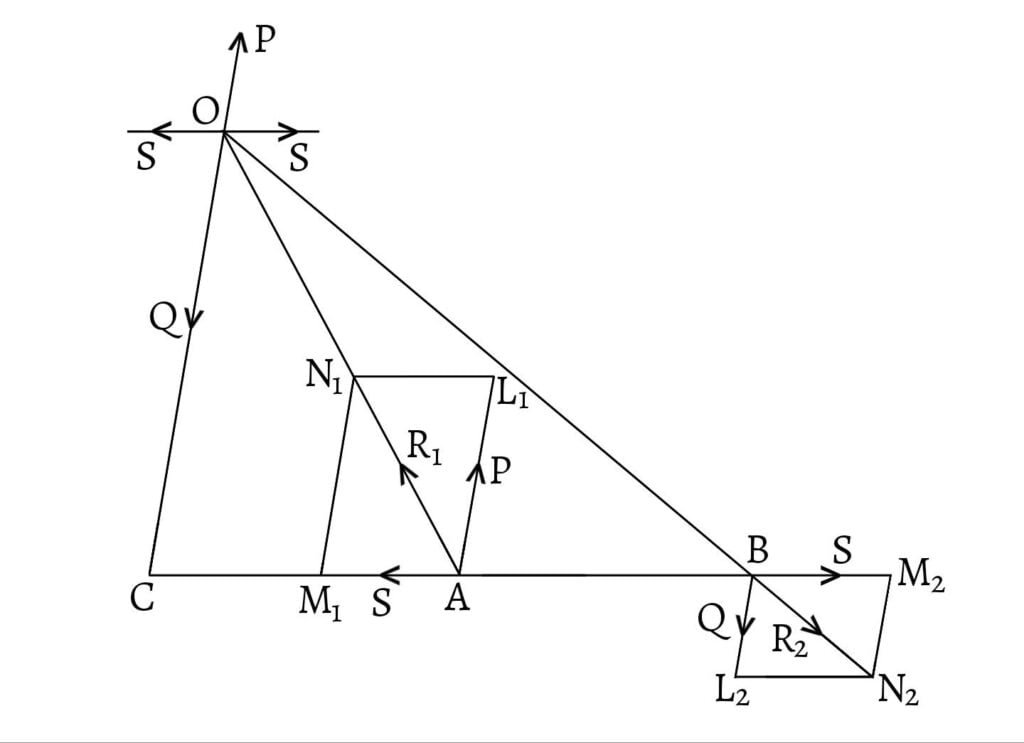
Apply two equal and opposite forces, each being equal to $S$ along $BA$ and $AB$ represented by $A{M}_1$ and $B{M}_2$ respectively. These two forces balance each other and have no impact upon the equilibrium of the body. Complete the parallelograms $A{L}_1{N}_1{M}_1$ and $B{L}_2{N}_2{M}_2$. Let the diagonals $N_{1}A$ and $N_{2}B$ be produced to meet at $O$. Through $O$, draw $OC$ parallel to $B{L}_2$ to meet $BA$ produced at $C$.

Now, the forces $P$ and $S$ at $A$ have a resultant $R_1$ represented by $A{N}_1$ and let its point of application be transferred to $O$. Similarly, the forces $Q$ and $S$ at $B$ have the resultant $R_2$ represented by $B{N}_2$ and let its point of application be transferred to $O$.

The force $R_1$ at $O$ can be resolved into two components; $S$ parallel to $A{M}_1$ and $P$ in the direction $CO$. Similarly, the force $R_2$ at $O$ may be resolved into two components; $S$ parallel to $B{M}_2$ and $Q$ in the direction $OC$.

Hence, the given forces are equivalent to two forces $P$ and $Q$ along $CO$ and two forces each equal to $S$ acting in opposite directions. The first two forces are equivalent to a single force $(P-Q)$ acting along $CO$ (i.e. acting at $C$ in the direction parallel to that of the force $P$) and the forces equal to $S$ balance one another.

Thus, the resultant of two unlike parallel forces $P$ and $Q$ $(P>Q)$ is equivalent to a force $(P+Q)$ acting in the direction of greater force.

The point of application of the resultant

The $\mathrm{\Delta }OCA$ and $\mathrm{\Delta }{N}_1{M}_{1}A$ are similar, $$\frac{OC}{N_1{M}_1}=\frac{CA}{M_{1}A}$$ $$\frac{OC}{A{L}_1}=\frac{CA}{A{M}_1}$$ $$\frac{OC}{P}=\frac{CA}{S}$$ $$S\times OC=P\times CA\text{ \_\_(1)}$$

The $\mathrm{\Delta }OCB$ and $B{L}_2{N}_2$ are similar, $$\frac{OC}{B{L}_2}=\frac{CB}{L_2{N}_2}$$ $$\frac{OC}{Q}=\frac{CB}{S}$$ $$S\times OC=Q\times CB\text{ \_\_(2)}$$ From $\text{(1)}$ and $\text{(2)}$, $$P\times CA=Q\times CB$$ $$\frac{CA}{CB}=\frac{Q}{P}$$ i.e. $C$ divides $AB$ externally in the inverse ratio of the forces.

Cor.1. $$\frac{P}{CB}=\frac{C}{CA}=\frac{P-Q}{CB-CA}=\frac{R}{AB}$$ If the forces $P$ and $Q$ are unlike and equal, the triangles $A{M}_1{N}_1$ and $B{M}_2{N}_2$ being equal in all respects, $\mathrm{\angle }{M}_{1}A{N}_1=\mathrm{\angle }{M}_{2}B{N}_2$. In this case, $A{N}_1$ and $N_{2}B$ will be parallel and not meet at any such point $O$. Hence, the geometrical condition for finding the resultant fails. Therefore, two equal and unlike parallel forces cannot be compounded into a single force.

Resultant of several parallel forces

There are many cases where a large number of parallel forces act at the same time on a body. These forces are found to combine together to form a single force, for example, the weight of the body.

A body is made up of several particles rigidly connected to one another. Each particle is attracted towards the centre of the earth i.e. each particle of the body has a weight. The line of action of the force is towards the centre of the earth. But the distance of each particle of the body from the centre of the earth is so great that the lines of action of the weights of all particles may be considered parallel to one another. So, all these parallel forces have a resultant which is the weight of the body.

Consider a thin straight rod having particles’ weights $w_1,w_2,\dots$ lying along a straight line at distances $x_1,x_2,\dots$ from a fixed point $O$ on the line.
∴The fixed resultant or the weight of the body is, $$w=w_1+w_2+\dots =\sum w_i$$ and the point of application of the weight is at a distance, $$\overline{x}=\frac{w_1{x}_1+w_2{x}_2+\dots }{w_1+w_2+\dots }$$$$=\frac{\sum w_i{x}_i}{\sum w_i}\text{ from O}$$

This point is a fixed point on the rod and is called the centre of gravity of the rod.
If the rigid body is a plane, then the weight of the body acts at a point $(\overline{x},\overline{y})$ such that, $$\overline{x}=\frac{\sum w_i{x}_i}{\sum w_i}\text{ and, }\overline{y}=\frac{\sum w_i{y}_i}{\sum w_i}$$ This point $(\overline{x},\overline{y})$ is a unique point which denotes the position of any one of the particles and is the centre of gravity of the body.
If a body is uniform and homogeneous having standard geometric shape, then its centre of gravity generally lies at its geometric centre.

---

Two parallel forces of $30\text{ kg wt.}$ and $20\text{ kg wt.}$ are acting at a distance $40\text{ cms}$ apart. Find their resultant if forces are like.

Let $R$ be the resultant of the forces and let it passes through a point $C$.

$$AB=40\text{ cms}$$ $$AC=x\text{ cm}$$ $$\therefore CB=(40-x)\text{ cm}$$

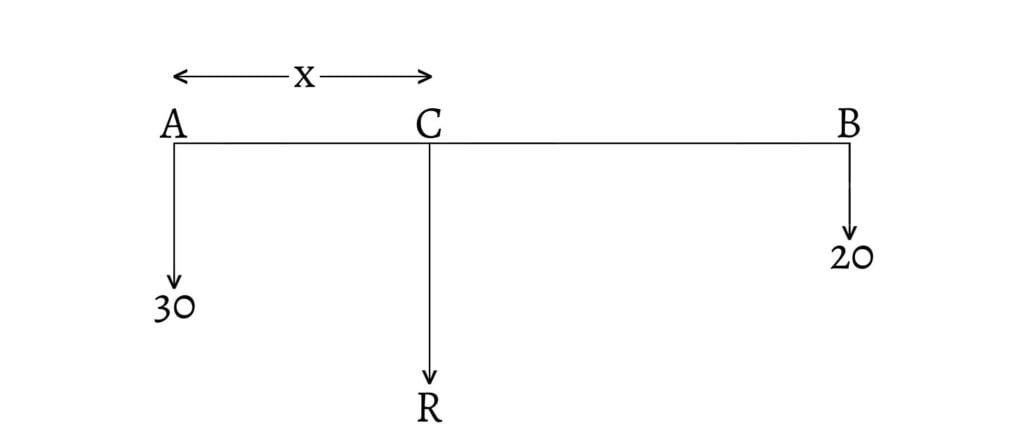
Since the forces are like and parallel, $$R=30+20=50\text{ kg wt.}$$ and, $$30\times AC=20\times CB$$ $$30x=20(40-x)$$ $$\therefore x=16\text{ cms}$$

Thus, the resultant force is $50\text{ kg wt.}$ which acts at a distance $16\text{ cms}$ from the point $A$.

---

A straight weightless rod, $48\text{ cms}$ in length, rests in a horizontal position between two pegs placed at a distance of $6\text{ cms}$ apart, one peg being at one end of the rod, and a weight of $2\text{ kg}$ is suspended from the other end. Find the pressure on the pegs.

Let $AB$ be a straight weightless rod resting between two pegs at $A$ and $C$.

$$AB=48\text{ cms}$$ $$AC=6\text{ cms}$$ $$CB=AB-AC=48-6=42\text{ cms}$$ Let the pressure on the pegs at $A$ and $C$ be $P$ and $Q$ respectively. When a weight of $2\text{ kg}$ is suspended at the end of $B$, the system is in equilibrium. Therefore, $2\text{ kg wt.}$ is the resultant of two unlike parallel forces $P$ and $Q$.

$$\therefore \frac{P}{CB}=\frac{Q}{AB}=\frac{2}{AC}$$ $$\frac{P}{42}=\frac{Q}{48}=\frac{2}{6}$$ $$\therefore P=\frac{42\times 2}{6}=14\text{ kg wt.}$$ $$\text{and, }Q=\frac{48\times 2}{6}=16\text{ kg wt.}$$

---

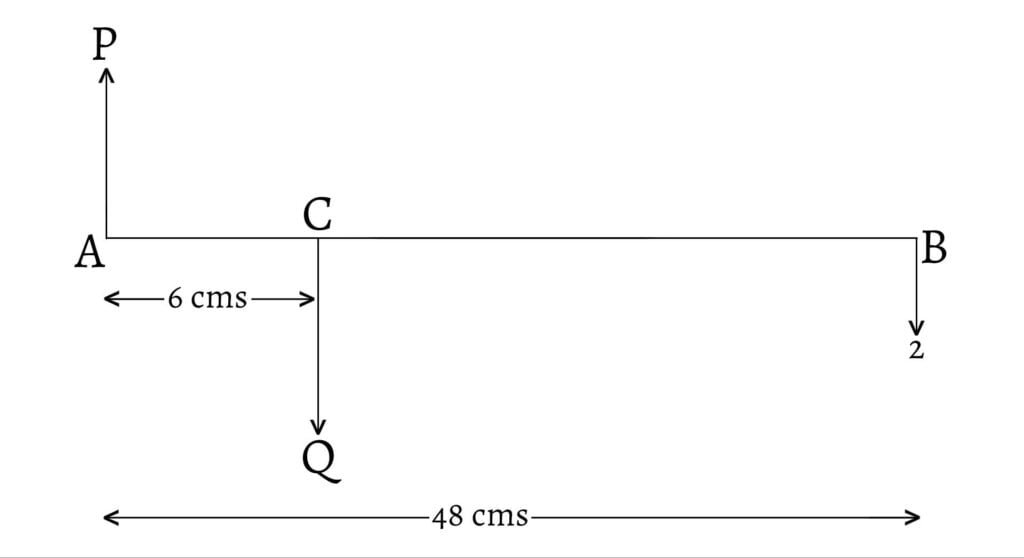
A man carries a bundle at the end of a stick which is placed over the shoulder. What is the distance between his hand and shoulder when the pressure on his shoulder is least?

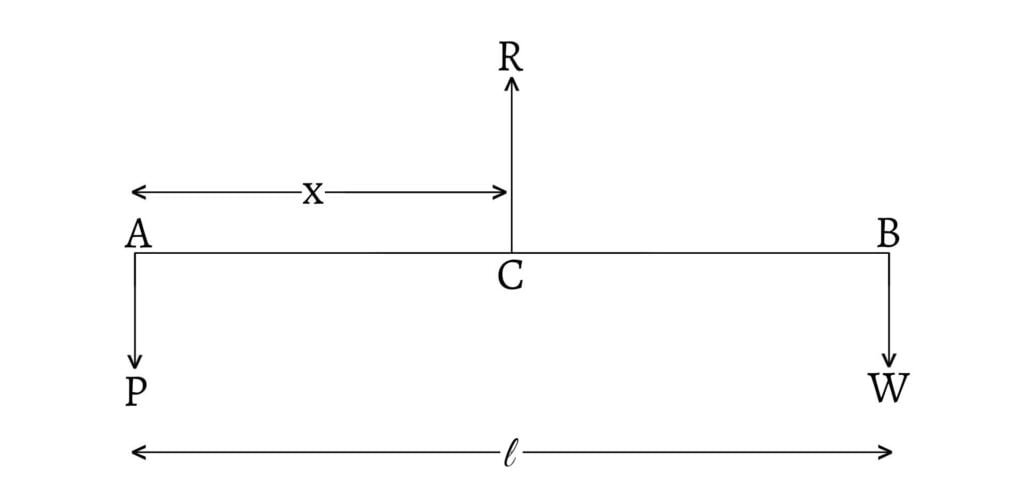
Let $AB$ be a stick of length $l$. Let the position of the shoulder be $C$. If $W$ be the bundle at the end $B$ and $P$ be the pressure due to the hand at $A$, then the shoulder is pressed to the resultant of $P$ and $W$. Let $R$ be the reaction on the shoulder $C$ and let $AC=x$.

Since the forces form the parallel forces, $$\frac{P}{CB}=\frac{W}{AC}=\frac{R}{AB}$$ $$\frac{P}{l-x}=\frac{W}{x}=\frac{R}{l}$$ $$\therefore R=\frac{Wl}{x}$$

Since, $Wl$ is a constant. So, $R$ depends upon $x$. And, we can see that $R$ will be least when $x$ will be greatest. The greatest value of $x$ is $l$. Hence, $R$ will be least when the distance between the hand and the shoulder is equal to the length of the stick.

---