Let $ƒ(x)$ and $g(x)$ be two functions of $x$ such that \[\lim_{x \to a} ƒ(x)=l\] \[\lim_{x \to a} g(x)=m\] then we have the following theorems on limit:
- The limit of the sum or difference of the functions $ƒ(x)$ and $g(x)$ is the sum or difference of the limits of the functions i.e. \[\lim_{x \to a} [ƒ(x)±g(x)]=\lim_{x \to a} ƒ(x) ± \lim_{x \to a} g(x)\]\[=l±m\]
- The limit of the product of the functions $ƒ(x)$ and $g(x)$ is the product of the limits of the functions i.e. \[\lim_{x \to a} [ƒ(x).g(x)]=\left(\lim_{x \to a} ƒ(x)\right).\left(\lim_{x \to a} g(x) \right)\] \[=l.m\]
- The limit of the quotient of the functions $ƒ(x)$ and $g(x)$ is the quotient of the limits of the functions, provided that the limit of the denominator is not zero i.e. \[\lim_{x \to a} \frac{ƒ(x)}{g(x)}=\frac{\lim_{x \to a} ƒ(x)} {\lim_{x \to a} g(x)}\] \[=\frac{l}{m} \text{ } \left(\lim_{x \to a} g(x)=m≠0\right)\]
- The limit of the $n^{\text{th}}$ root of a function $ƒ(x)$ is the $n^{\text{th}}$ root of the limit of the function i.e. \[\lim_{x \to a} \sqrt[n]{ƒ(x)}=\sqrt[n]{\lim_{x \to a} ƒ(x)}=\sqrt[n]{l}\]
An important theorem on limit
For all rational values of $n$, \[\lim_{x \to a} \frac{x^n-a^n}{x-a}=na^{n-1}\]
The proof of this theorem consists of the following three cases:
Case I: When $n$ is a positive integer: \[\frac{x^n-a^n}{x-a}\]\[=x^{n-1}+x^{n-2}.a+x^{n-3}.a^2+…+a^{n-1}\]
Now, \[\lim_{x \to a} \frac{x^n-a^n}{x-a}\]\[=\lim_{x \to a} [x^{n-1}+x^{n-2}.a+x^{n-3}.a^2+…+a^{n-1}]\] \[=a^{n-1}+a^{n-1}+a^{n-1}+…+a^{n-1}\] \[=na^{n-1}\]
Case II: When $n$ is a negative integer:
Let $n=-m$ where $m$ is a positive integer. Then, \[\lim_{x \to a} \frac{x^n-a^n}{x-a}=\lim_{x \to a} \frac{x^{-m}-a^{-m}}{x-a}\] \[=\lim_{x \to a} \frac{\frac{1}{x^m}-\frac{1}{a^m}} {x-a}\] \[=\lim_{x \to a} \frac{a^m-x^m}{x^ma^m(x-a)}\] \[=\lim_{x \to a} \left[-\frac{x^m-a^m}{x-a}×\frac{1}{x^ma^m}\right]\] \[=-\left(\lim_{x \to a} \frac{x^m-a^m}{x-a}\right) \left(\lim_{x \to a} \frac{1}{x^ma^m}\right)\] \[=-m.a^{m-1}\frac{1}{a^m.a^m} \text{ (using case I)}\] \[=(-m)a^{(-m)-1}\] \[=na^{n-1}\]
Case III: When $n$ is a rational fraction:
Let $n=\frac{p}{q}$ where $p$ and $q$ are integers and $q≠0$. Then, \[\lim_{x \to a} \frac{x^n-a^n}{x-a}=\lim_{x \to a} \frac{x^{\frac{p}{q}}-a^{\frac{p}{q}}}{x-a}\] \[=\lim_{x \to a} \frac{x^{(\frac{1}{q})p}-a^{(\frac{1}{q})p}}{x-a}\]
Put $x^{\frac{1}{q}}=y$ and $a^{\frac{1}{q}}=b$ so that $x=y^q$ and $a=b^q$. When $x\to a$, $y \to b$.
Now, \[\lim_{x \to a} \frac{x^n-a^n}{x-a}=\lim_{y \to b} \frac{y^p-b^p}{y^q-b^q}=\lim_{y \to b} \frac{\frac{y^p-b^p}{y-b}} {\frac{y^q-b^q}{y-b}}\] \[=\frac{\lim_{y \to b} \frac{y^p-b^p}{y-b}} {\lim_{y \to b} \frac{y^q-b^q}{y-b}}=\frac{p.b^{p-1}} {q.b^{q-1}}=\frac{p}{q}b^{p-q}\]\[=\frac{p}{q}b^{q(\frac{p}{q}-1)}=\frac{p}{q}(b^q)^{\frac{p}{q}-1}=na^{n-1}\]
Therefore, for all rational values of $n$, \[\lim_{x \to a} \frac{x^n-a^n}{x-a}=na^{n-1}\]
Limits of Algebraic Functions
Example 1: Find the limiting value of $ƒ(x)=3x^2-5x+6$ when $x\to 2$. \[\lim_{x \to 2} (3x^2-5x+6)=12-10+6=8\]
Example 2: Evaluate \[\lim_{x \to 0} \frac{5x^2+3x}{x}\]
When $x=0$, the given function takes the indeterminate form $\frac{0}{0}$. But, \[\lim_{x \to a}\frac{5x^2+3x}{x}=\lim_{x \to 0} \frac{x(5x+3)}{x}\] \[=\lim_{x \to 0} (5x+3)=0+3=3\]
Example 3: Evaluate \[\lim_{x \to \infty} \frac{3x^2+2x+1}{4x^2+x+5}\]
When $x=\infty$, the given function takes the indeterminate form $\frac{\infty}{\infty}$. Therefore, \[\lim_{x \to a} \frac{3+\frac{2}{x}+\frac{1}{x^2}}{4+\frac{1}{x}+\frac{5}{x^2}}=\frac{3+0+0}{4+0+0}=\frac{3}{4}\]
Example 4: Evaluate \[\lim_{x \to \infty} (\sqrt{x+a}-\sqrt{x})\]
When $x=\infty$, the given function takes the indeterminate form $\infty-\infty$. But, \[\lim_{x \to \infty} (\sqrt{x+a}-\sqrt{x})\]\[=\lim_{x \to \infty} \frac{(\sqrt{x+a}-\sqrt{x})(\sqrt{x+a}+\sqrt{x})}{(\sqrt{x+a}+\sqrt{x})}\] \[=\lim_{x \to \infty} \frac{x+a-x}{\sqrt{x+a}+\sqrt{x}}=\lim_{x \to \infty} \frac{a}{\sqrt{x+a}+\sqrt{x}}\] \[=\frac{a}{\infty+\infty}=\frac{a}{\infty}=0\]
Limits of Trigonometric Functions
\[\text{1. } \lim_{\theta \to 0} \sin\theta = 0\text{ and, 2. } \lim_{\theta \to 0}\cos\theta=1\]
Let $\angle AOB=\theta$. Take any point $P$ on the line $OB$. From $P$ draw $PM$ perpendicular to $OA$.

Then, \[\sin\theta=\frac{MP}{OP}\text{ and }\cos\theta=\frac{OM}{OP}\] When $\theta$ is small, $MP$ will be small and $P$ will be near to $M$. When $\theta$ is small enough, $MP$ will be small enough and $P$ will be very close to $M$. This implies that as $\theta \to 0$, $MP\to 0$ and $OP\to OM$. \[\therefore \lim_{\theta \to 0} \sin\theta=\lim_{\theta \to 0} \frac{MP}{OP}=0\] \[\lim_{\theta \to 0} \cos\theta=\lim_{\theta \to 0} \frac{OM}{OP}=1\] $\text{3. } \lim_{\theta \to \alpha} \sin\theta=\sin\alpha$
Put $\theta=\alpha+h$ so that when $\theta \to \alpha$, $h\to 0$. Now, \[\lim_{\theta \to \alpha} \sin\theta =\lim_{h \to 0} \sin(\alpha+h)\] \[=\lim_{h \to 0} [sin\alpha\cosh+\cos\alpha\sinh]\] \[=\sin\alpha \lim_{h \to 0} \cos h + \cos\alpha\lim_{h \to 0} \sin h\] \[=\sin\alpha.1+\cos\alpha.0\]\[=\sin\alpha\] \[\therefore \lim_{\theta \to \alpha} \sin\theta = \sin\alpha\]
Theorem: \[\lim_{\theta \to 0} \frac{\sin\theta}{\theta}=1\] Where $\theta$ is measured in radian.
Let $AB$ be a diameter of a circle with centre at $O$ and radius $r$. Take any point $P$ on the circle which is very close to $B$ so that $\theta \to 0$. Join $P$ and $B$ and draw $PN$ perpendicular to $OB$.
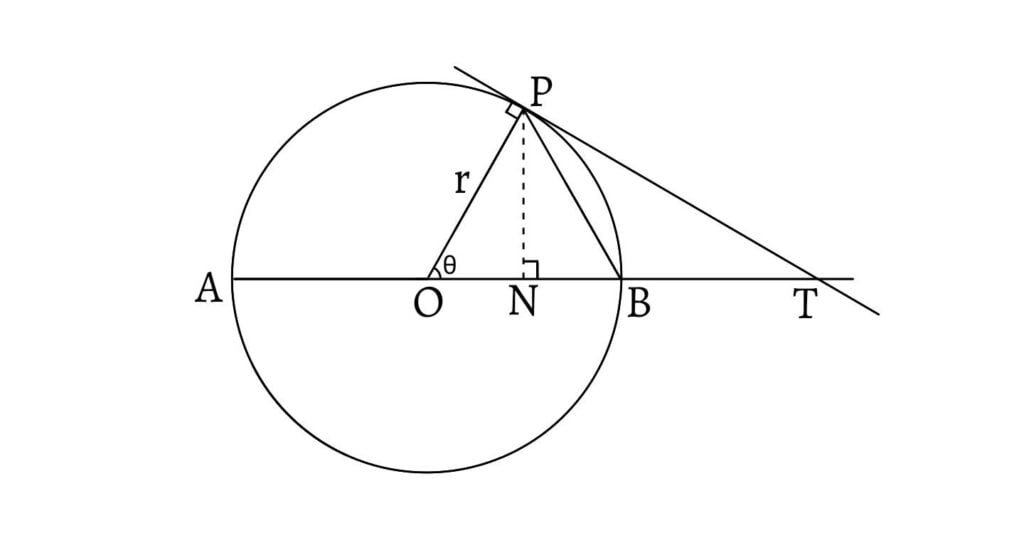
Then, \[∆OPB≤\text{Area of sector OPB}≤∆OPT\] Now, \[∆OPB=\frac{1}{2}OB.PN=\frac{1}{2}r.r\sin\theta\]\[=\frac{1}{2}r^2\sin\theta\] \[\text{Area of sector OPB}=\frac{1}{2}lr\] \[=\frac{1}{2}r.r\theta=\frac{1}{2}r^2 \theta\] \[∆OPT=\frac{1}{2}OP.PT\] \[=\frac{1}{2}r.r\tan\theta=\frac{1}{2}r^2\tan\theta\] \[\therefore \frac{1}{2}r^2\sin\theta≤\frac{1}{2}r^2\theta≤\frac{1}{2}r^2\tan\theta\] \[\sin\theta≤\theta≤\tan\theta\] \[1≤\frac{\theta}{\sin\theta}≤\frac{1}{\cos\theta}\] \[1≥\frac{\sin\theta}{\theta}≥\cos\theta\] Making $\theta \to 0$, \[\lim_{\theta \to 0} 1 ≥ \lim_{\theta \to 0} \frac{\sin\theta}{\theta} ≥ \lim_{\theta \to 0} \cos\theta\] \[1≥\lim_{\theta \to 0} \frac{\sin\theta}{\theta}≥1\] \[1=\lim_{\theta \to 0} \frac{\sin\theta}{\theta}=1\] \[\therefore \lim_{\theta \to 0} \frac{\sin\theta}{\theta}=1\]
Also, $\text{1. } \lim_{\theta \to 0} \frac{\theta}{\sin\theta}=1$ \[\lim_{\theta \to 0} \frac{\theta}{\sin\theta}=\lim_{\theta \to 0} \frac{1}{\frac{\sin\theta}{\theta}}=\frac{1}{\lim_{\theta \to 0}\frac{sin\theta}{\theta}}=1\] $\text{2. } \lim_{\theta \to 0}\frac{\tan\theta}{\theta}=1$ \[\lim_{\theta \to 0} \frac{\tan\theta}{\theta}=\lim_{\theta \to 0} \frac{\sin\theta}{\theta\cos\theta}\]\[=\lim_{\theta \to 0} \frac{\sin\theta}{\theta}\lim_{\theta \to 0} \frac{1}{\cos\theta}=1.\frac{1}{\cos 0}=1\]
Limits of Logarithmic and Exponential Functions
According to the definition of $e$, \[e=\lim_{n \to \infty} \left(1+\frac{1}{n}\right)^n\] Putting $n=\frac{1}{h}$ so that when $n\to \infty$, $h\to 0$, then \[\lim_{n \to \infty}\left(1+\frac{1}{n}\right)^n=\lim_{h \to 0}(1+h)^{\frac{1}{h}}=e\] $\text{1. } \lim_{x \to 0} \frac{\log(1+x)}{x}=1$ \[\lim_{x \to 0} \frac{\log(1+x)}{x}=\lim_{x \to 0}\frac{1}{x}\log(1+x)\] \[=\lim_{x \to 0} \log(1+x)^{\frac{1}{x}}\] \[=\log \left\{\lim_{x \to 0}(1+x)^{\frac{1}{x}}\right\}=\log e=1\] $\text{2 .} \lim_{x \to 0} \frac{e^x-1}{x}=1$
Put $e^x-1=y$, then, $e^x=1+y$ and $x=\log(1+y)$ so that when $x\to 0$, $y\to 0$. \[\lim_{x \to 0}\frac{e^x-1}{x}=\lim_{y \to 0} \frac{y}{\log(1+y)}\] \[=\lim_{y \to 0} \frac{1}{\frac{1}{y}\log(1+y)}=\frac{1}{1}=1\] $\text{3. }\lim_{x \to 0} \frac{a^x-1}{x}=\log a$
Put $a^x-1=y$, then, $a^x=1+y$ which implies $x\log a=\log(1+y)$ and $x=\frac{\log(1+y)}{\log a}$ so that when $x\to 0$, $y\to 0$. \[\lim_{x \to 0} \frac{a^x-1}{x}=\lim_{y \to 0} \frac{y}{\frac{\log(1+y)}{\log a}}\] \[=\log a\lim_{y \to 0} \frac{1}{\frac{1}{y}\log(1+y)}\] \[=\log a.1=\log a\]
Previous: Limit of a Function
Next: Continuity
Explore Derivatives
- Origin of Differential Calculus
- Derivative
- Techniques of Differentiation
- Derivatives of Trigonometrical Functions
- Derivatives of Inverse Circular Functions
- Derivatives of Logarithmic and Exponential Functions
- Derivatives of Hyperbolic and Inverse Hyperbolic Functions
