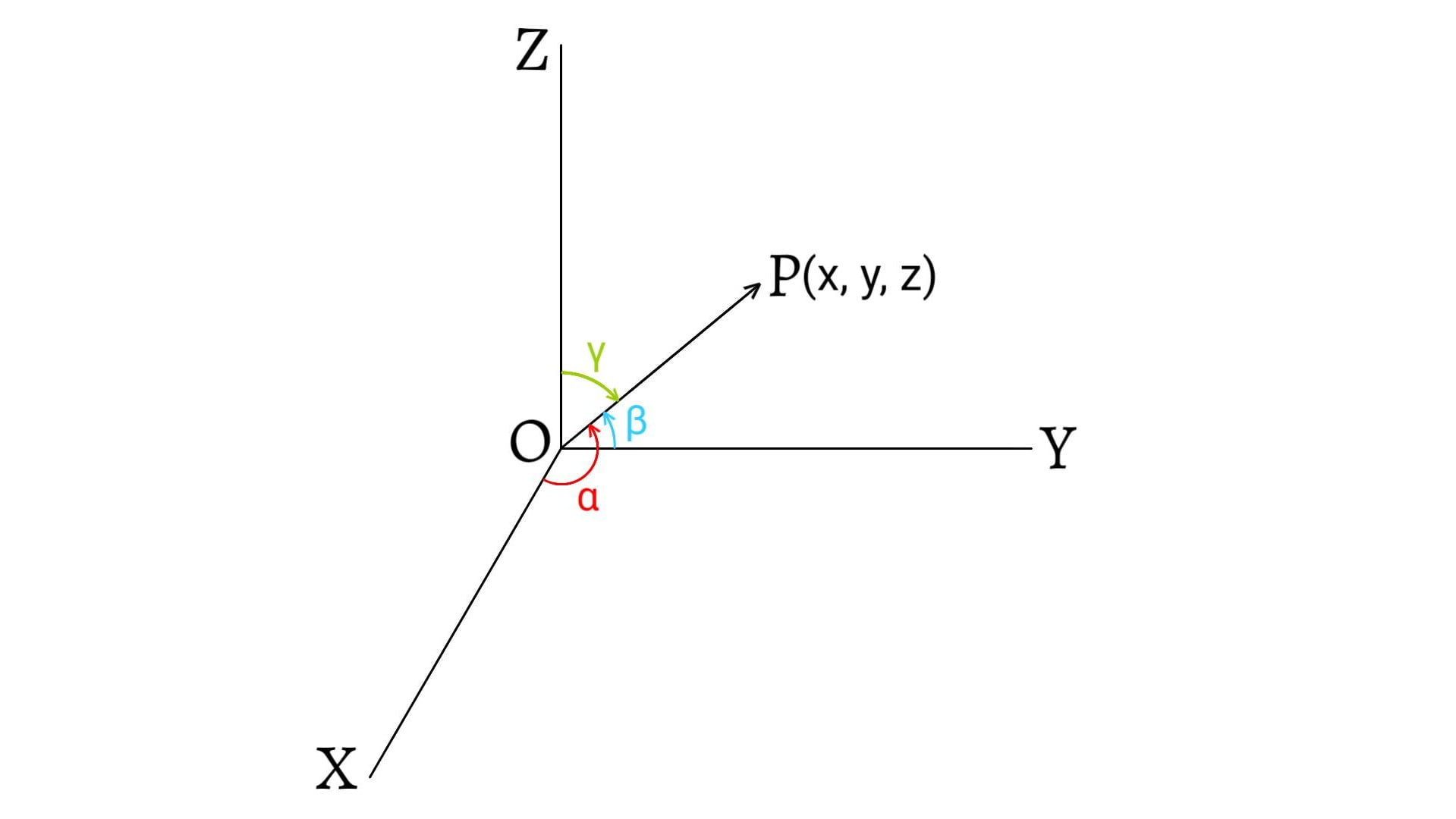
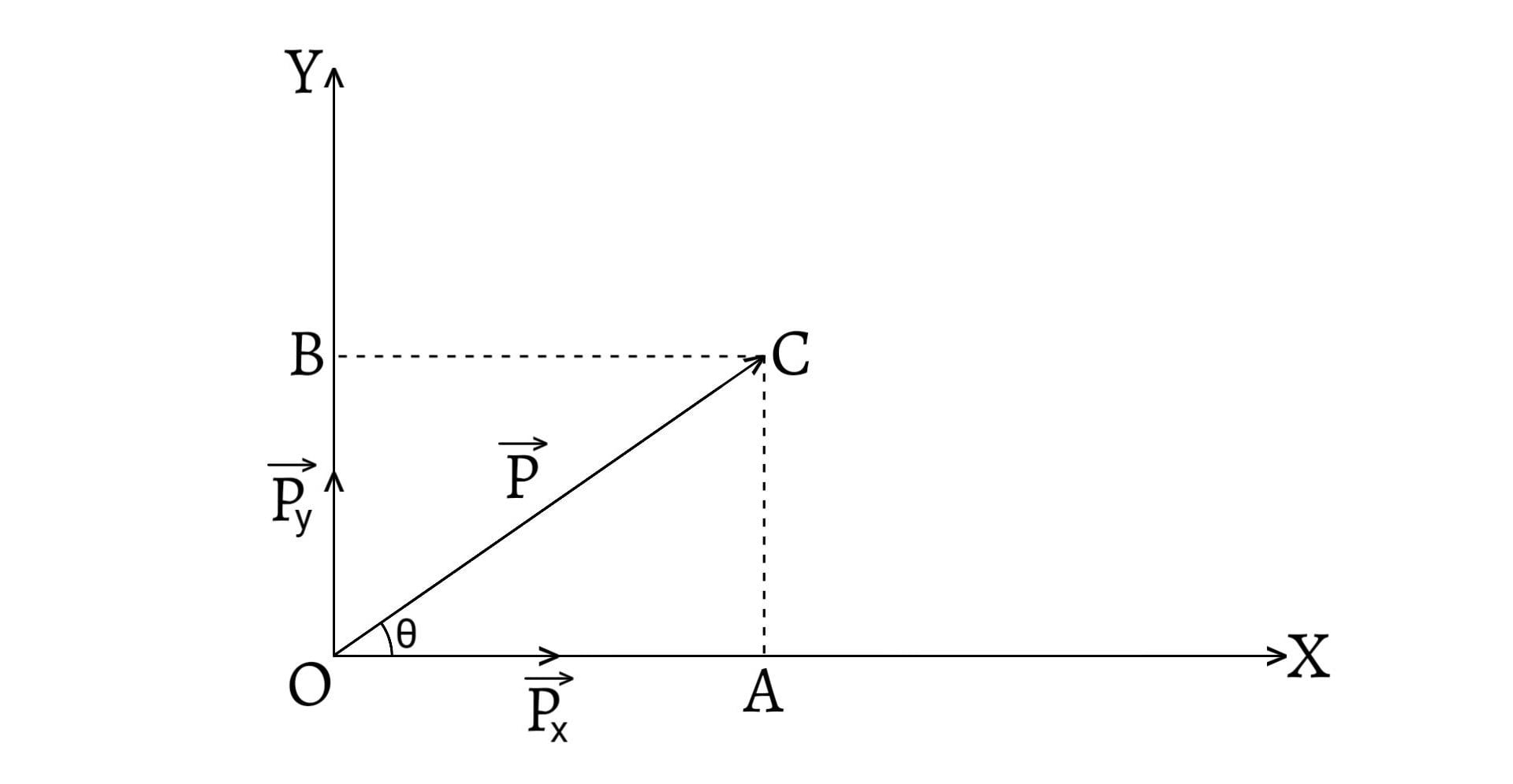
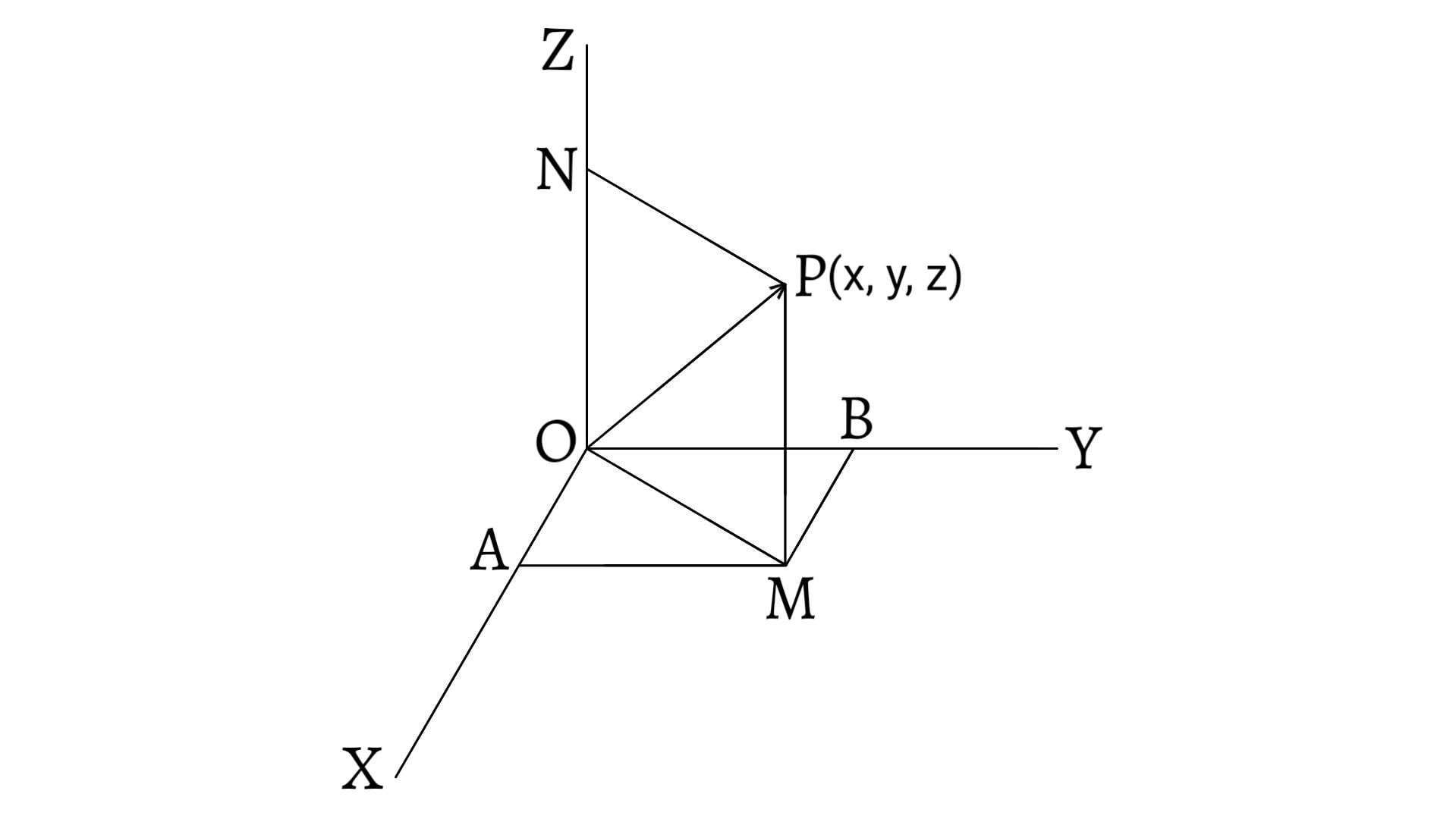
Polygon law of vectors states that if a particle simultaneously possesses a number of vectors which are represented in magnitude and direction by the sides of a polygon taken in order, then their resultant vector is represented both in magnitude and direction by the closing side of the polygon taken in opposite order.
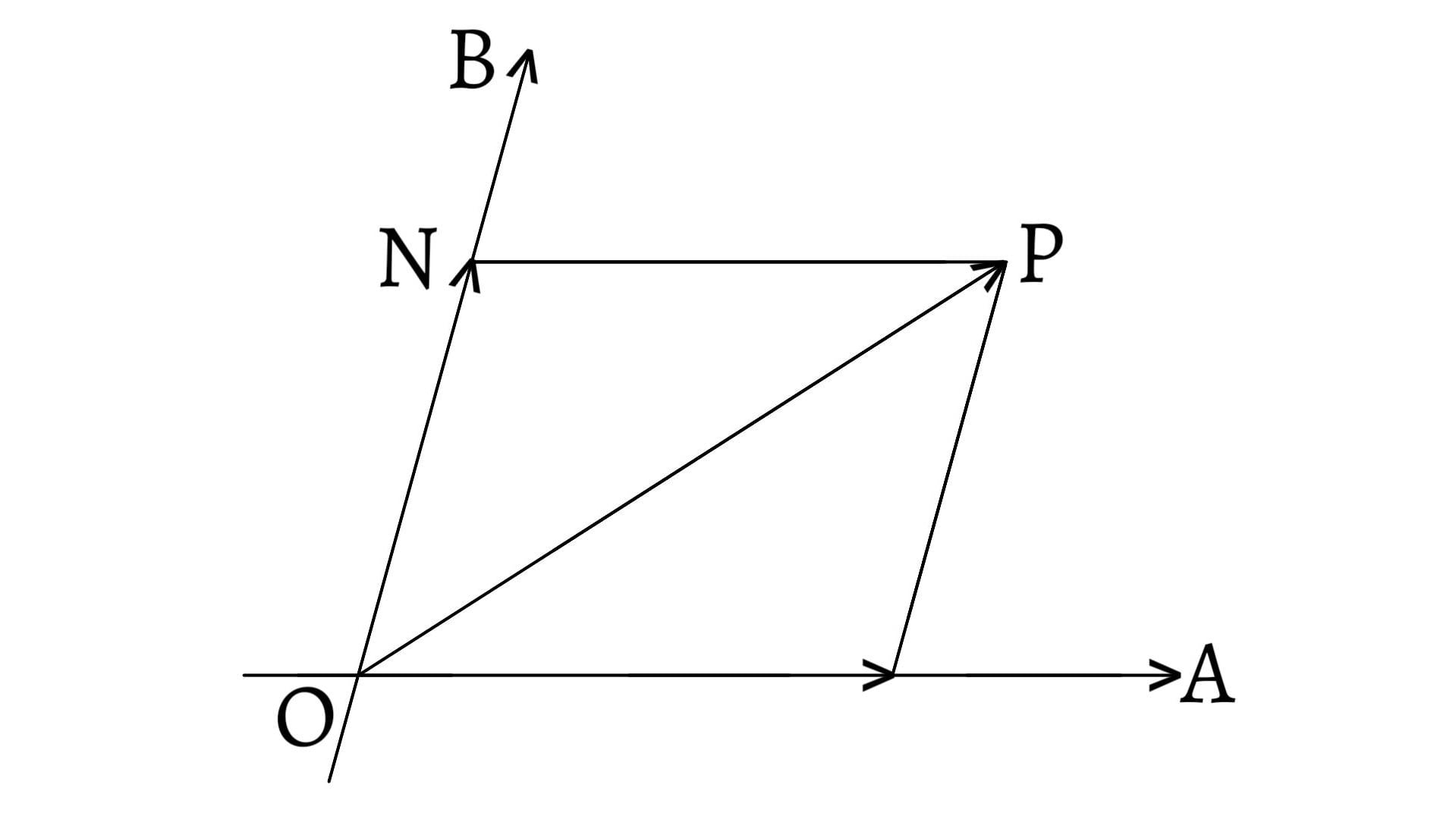
Consider a particle $O$ which possesses vectors $\overrightarrow{u}$, $\overrightarrow{v}$, $\overrightarrow{w}$, $\overrightarrow{x}$ and $\overrightarrow{y}$ simultaneously.
Draw a vector $\overrightarrow{AB}$ parallel and equal to $\overrightarrow{u}$ such that $\overrightarrow{AB}$ represents the vector $\overrightarrow{u}$ of the particle both in magnitude and direction. Similarly, represent the magnitude and direction of the vectors $\overrightarrow{v}$, $\overrightarrow{w}$, $\overrightarrow{x}$ and $\overrightarrow{y}$ by $\overrightarrow{BC}$, $\overrightarrow{CD}$, $\overrightarrow{DE}$ and $\overrightarrow{EF}$ respectively.
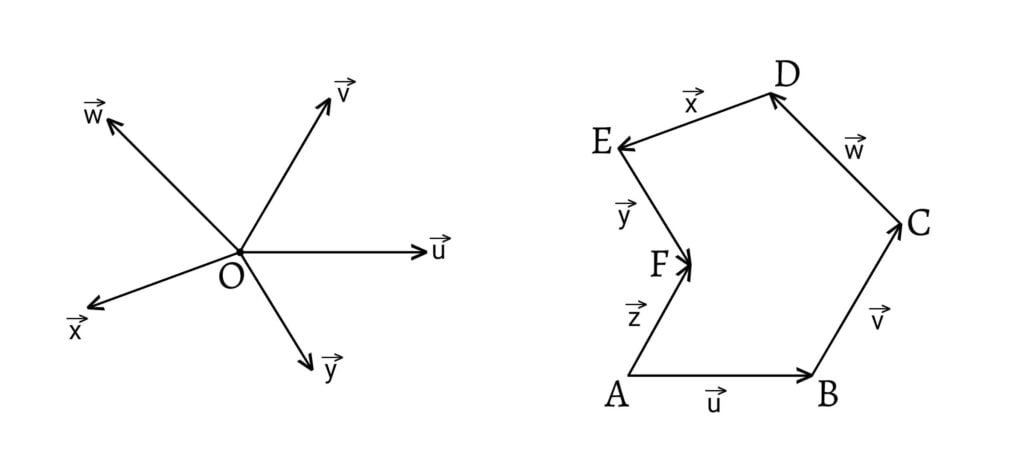
Now, join $AF$. Then, the resultant $\overrightarrow{z}$ of the vectors $\overrightarrow{u}$, $\overrightarrow{v}$, $\overrightarrow{w}$, $\overrightarrow{x}$ and $\overrightarrow{y}$ is represented in magnitude and direction by the vector $\overrightarrow{AF}$, the closing side of the polygon.
\[\therefore\overrightarrow{AF}=\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DE}+\overrightarrow{EF}\]
\[\text{or,}\;\overrightarrow{z}=\overrightarrow{u}+\overrightarrow{v}+\overrightarrow{w}+\overrightarrow{x}+\overrightarrow{y}\]
If the particle possesses a number of vectors which can be represented in magnitude and direction by the sides of a closed polygon taken in order then the particle is in equilibrium state.
Represent the vectors $\overrightarrow{u}$, $\overrightarrow{v}$, $\overrightarrow{w}$, $\overrightarrow{x}$, $\overrightarrow{y}$ and $\overrightarrow{z}$ of the particle $O$ in magnitude and direction by the sides $\overrightarrow{AB}$, $\overrightarrow{BC}$, $\overrightarrow{CD}$, $\overrightarrow{DE}$, $\overrightarrow{EF}$ and $\overrightarrow{FA}$ of the closed polygon $ABCDEF$.

We know that the resultant of $\overrightarrow{u}$, $\overrightarrow{v}$, $\overrightarrow{w}$, $\overrightarrow{x}$ and $\overrightarrow{y}$ must have the same magnitude but opposite direction as that of $\overrightarrow{z}$.
\[\overrightarrow{u}+\overrightarrow{v}+\overrightarrow{w}+\overrightarrow{x}+\overrightarrow{y}+\overrightarrow{z}\]
\[=-\overrightarrow{z}+\overrightarrow{z}=0\]
Hence, the result of $\overrightarrow{u}$, $\overrightarrow{v}$, $\overrightarrow{w}$, $\overrightarrow{x}$, $\overrightarrow{y}$ and $\overrightarrow{z}$ will be zero and the particle will be in equilibrium state.
Previous: Triangle Law of Vector Addition
Next: Resolution of a Vector