A vector whose magnitude is unity is called a unit vector. Hence, if $|\overrightarrow{OP}|=1$, then $\overrightarrow{OP}$ is said to be a unit vector. The examples of unit vectors are $(1,0)$ and $(0,1)$.
Unit vector is dimensionless and represents only direction. The unit vector of a non zero vector $\overrightarrow{A}$ in the direction of $\overrightarrow{A}$ is represented by $\hat{A}$ (read A-cap or A-hat) and is given by \[\hat{A}=\frac{\overrightarrow{A}}{|\overrightarrow{A}|}\]
Hence, if $\overrightarrow{A}=(a_1,a_2)≠0$ then the unit vector $\hat{A}$ in the direction of $\overrightarrow{A}$ is defined by \[\left(\frac{a_1}{\sqrt{a_1^2+a_2^2}},\frac{a_2}{\sqrt{a_1^2+a_2^2}}\right)\]
The unit vectors along X, Y and Z axes of Cartesian coordinates system are represented by $\hat{i}$, $\hat{j}$ and $\hat{k}$ respectively.
The Unit Vectors $\overrightarrow{i}$, $\overrightarrow{j}$ and $\overrightarrow{k}$
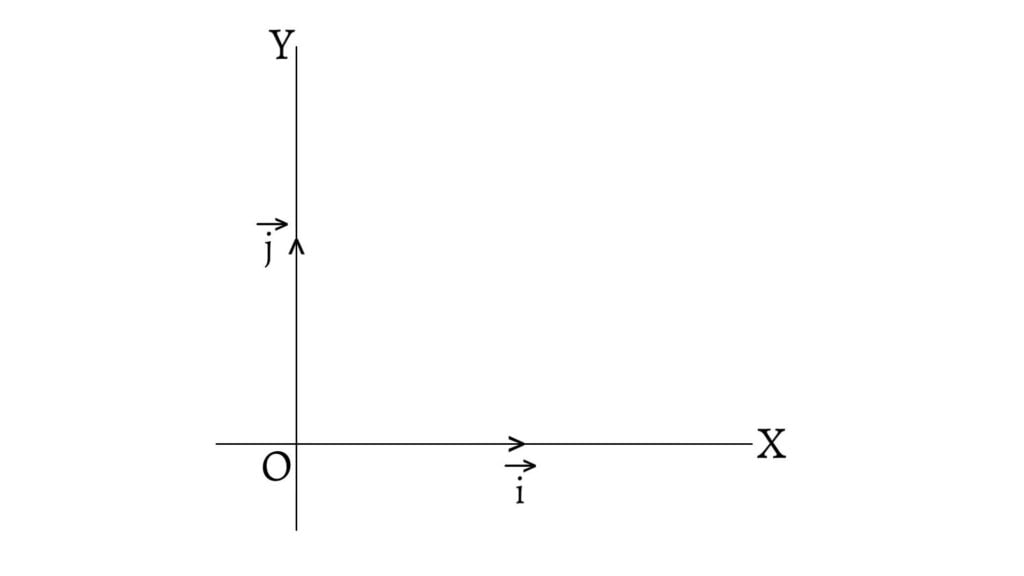
Let $\overrightarrow{i}$ and $\overrightarrow{j}$ be the unit vectors along two mutually perpendicular straight lines $OX$ and $OY$ respectively. Then, $\overrightarrow{i}$ and $\overrightarrow{j}$ are defined by,
\[\overrightarrow{i}=(1,0)\] \[\overrightarrow{j}=(0,1)\]

Again, let $\overrightarrow{i}$, $\overrightarrow{j}$ and $\overrightarrow{k}$ be the unit vectors along three mutually perpendicular straight lines $OX$, $OY$ and $OZ$ respectively. Then, $\overrightarrow{i}$, $\overrightarrow{j}$ and $\overrightarrow{k}$ are defined by,
\[\overrightarrow{i}=(1,0,0)\] \[\overrightarrow{j}=(0,1,0)\] \[\overrightarrow{k}=(0,0,1)\]
Theorem: Every plane vector is of the form $a_1\overrightarrow{i}+a_2\overrightarrow{j}$ and conversely.
Let $(a_1,a_2)$ be a plane vector. Then, \[(a_1,a_2)=(a_1+0,0+a_2)\] \[=(a_1,0)+(0,a_2)\] \[=a_1(1,0)+a_2(0,1)\] \[=a_1\overrightarrow{i}+a_2\overrightarrow{j}\] The converse part easily follows by the definitions of $\overrightarrow{i}$ and $\overrightarrow{j}$.
Theorem: Every space vector is of the form $a_1\overrightarrow{i}+a_2\overrightarrow{j}+a_3\overrightarrow{k}$ and conversely.
Let $(a_1,a_2,a_3)$ be a space vector. Then, \[(a_1,a_2,a_3)=(a_1+0+0,0+a_2+0,0+0+a_3)\] \[=(a_1,0,0)+(0,a_2,0)+(0,0,a_3)\] \[=a_1(1,0,0)+a_2(0,1,0)+a_3(0,0,1)\] \[=a_1\overrightarrow{i}+a_2\overrightarrow{j}+a_3\overrightarrow{k}\]
The converse part easily follows by the definitions of $\overrightarrow{i}$, $\overrightarrow{j}$ and $\overrightarrow{k}$.
Unit Vector of a Space Vector or a Line
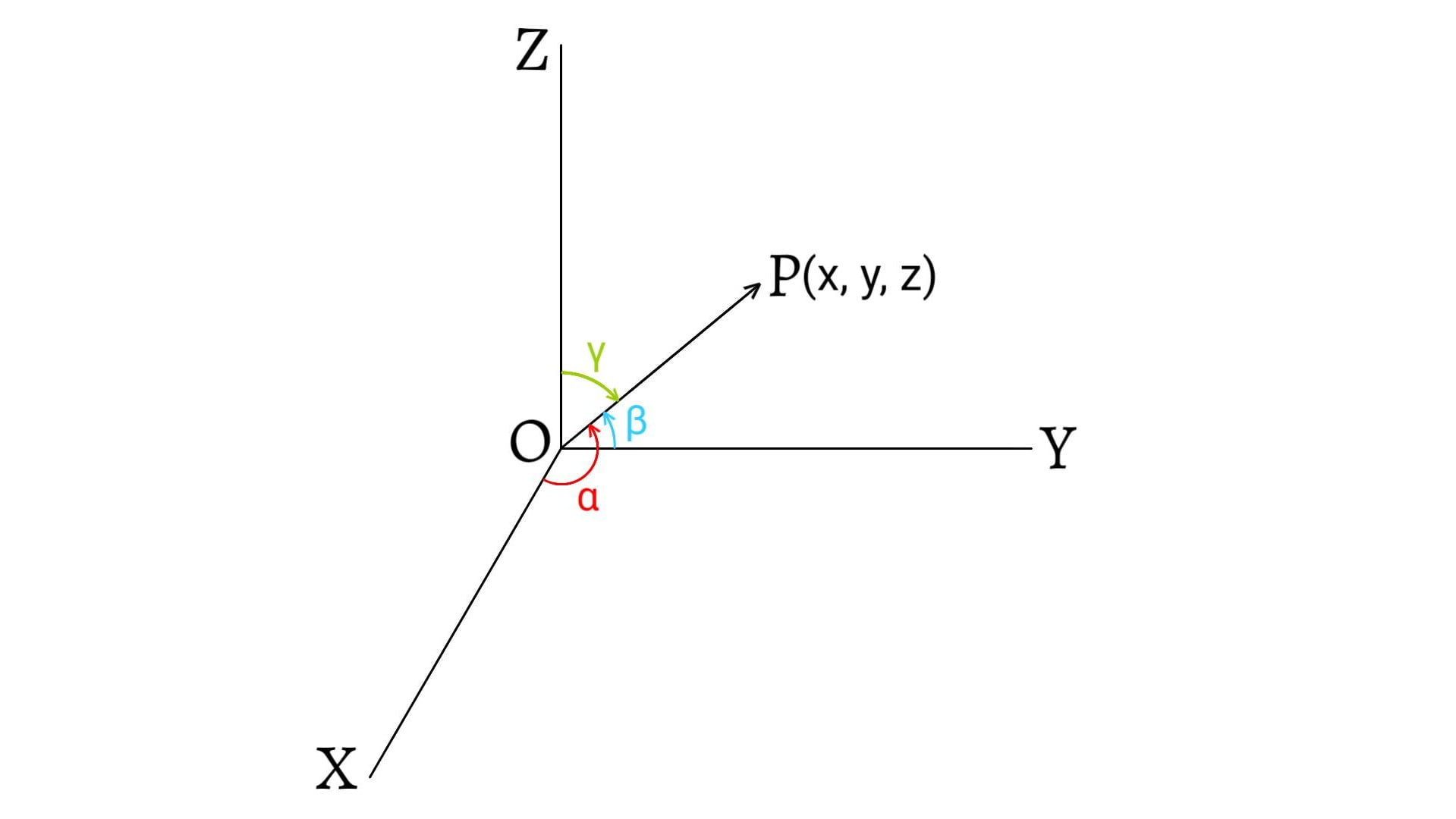
Let $O$ be the origin. Let $P(x,y,z)$ be a point in space. Then, \[\overrightarrow{OP}=(x,y,z) =x\:\overrightarrow{i}+y\:\overrightarrow{j}+z\:\overrightarrow{k}\] and, modulus of $\overrightarrow{OP}$ is given by \[|\overrightarrow{OP}=\sqrt{x^2+y^2+z^2}\]
Then, the unit vector along $\overrightarrow{OP}$ denoted by $\hat{OP}$ is defined by, \[\hat{OP}=\frac{\overrightarrow{OP}}{|\overrightarrow{OP}|}=\frac{ x\:\overrightarrow{i}+y\:\overrightarrow{j}+z\:\overrightarrow{k}}{\sqrt{x^2+y^2+z^2}}\]
\[=\frac{x}{\sqrt{x^2+y^2+z^2}}\overrightarrow{i}+\frac{y}{\sqrt{x^2+y^2+z^2}}\overrightarrow{j} +\frac{z}{\sqrt{x^2+y^2+z^2}}\overrightarrow{k}\] \[=\left(\frac{x}{\sqrt{x^2+y^2+z^2}},\frac{y}{\sqrt{x^2+y^2+z^2}},\frac{z}{\sqrt{x^2+y^2+z^2}}\right)\]
Previous: Zero Vector (Null Vector)
Next: Collinear Vectors