Double Intercept Form

Here, we will discuss about the double intercept form of the equation of straight lines.

Let a straight line intersect x-axis and y-axis at $A(a,0)$ and $B(0,b)$ respectively. Then, the intercepts on the x-axis and y-axis are $OA=a$ and $OB=b$ respectively. Also, let $P(x,y)$ be any point on $AB$.

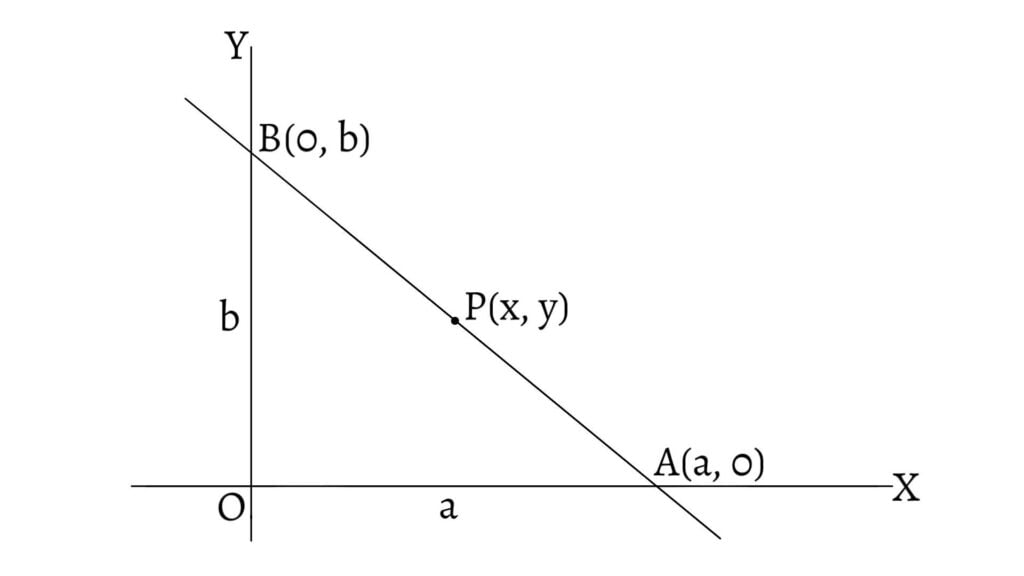
Then, \[\text{Slope of AP}=\text{Slope of PB}\] \[\frac{y-0}{x-a}=\frac{b-y}{0-x}\] \[\frac{y}{x-a}=\frac{b-y}{-x}\] \[-xy=bx-xy-ab+ay\] \[ab=bx+ay\] \[1=\frac{x}{a}+\frac{y}{b}\] \[\therefore\frac{x}{a}+\frac{y}{b}=1\]

This is the equation of the line whose intercepts are $a$ and $b$ and is known as the double intercept form. This form of the equation of a straight line cannot be used if the line passes through the origin or if it be parallel to any one of the axes.

---

Obtain the equation of the straight line passing through the point $(3,4)$ cutting off equal intercepts on the axes.

Here, \[\text{x-intercept}=\text{y-intercept}\] \[\therefore a=b\] Then the equation of the line is, \[\frac{x}{a}+\frac{y}{b}=1\] \[\frac{x}{a}+\frac{y}{a}=1\] \[x+y=a\text{ __(1)}\]

Since this line passes through the point $(3,4)$, \[3+4=a\] \[\therefore a=7\]

Putting the value of $a$ in $\text{(1)}$, \[x+y=7\] which is the required equation of the line.

---

Find the equation of the straight line which passes through the point $(3,4)$ and makes intercepts on the axes, the sum of whose lengths is $14$.

\[\text{Let x-intercept}=a\] \[\text{y-intercept}=b\] \[\text{Then, }a+b=14\] \[b=14-a\text{ __(1)}\]

The equation of the line is, \[\frac{x}{a}+\frac{y}{b}=1\] \[bx+ay=ab\] Since this line passes through $(3,4)$, \[3b+4a=ab\text{ __(2)}\]

Solving $\text{(1)}$ and $\text{(2)}$, \[3(14-a)+4a=a(14-a)\] \[42-3a+4a=14a-a^2\] \[a^2-13a+42=0\] \[(a-6)(a-7)=0\] \[\therefore a=6,7\]

Taking $a=6$, $b=14-6=8$. Then, the required equation of the line is \[\frac{x}{6}+\frac{y}{8}=1\] \[\therefore 4x+3y=24\]

Taking $a=7$, $b=14-7=7$. Then, the required equation of the line is, \[\frac{x}{7}+\frac{y}{7}=1\] \[\therefore x+y=7\]

---

Determine the equation of the line the portion of which, intercepted by the axes, is divided by the point $(-5,4)$ in the ratio $1:2$.

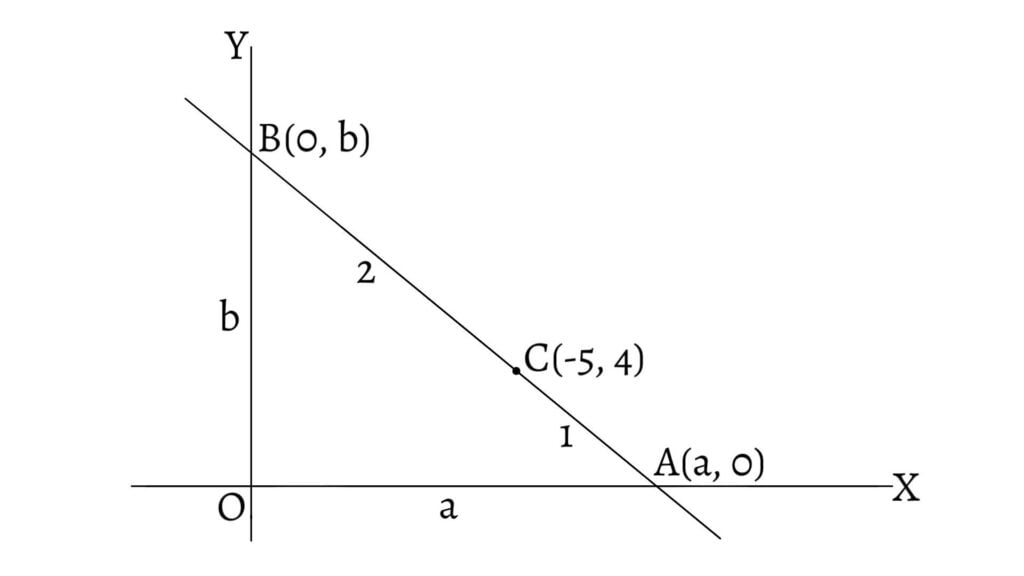
Let the line intersect x-axis and y-axis at $A(a,0)$ and $B(0,b)$ respectively and $AB$ is divided at $C$ in the ratio $1:2$. Then, from section formula for internal division, we have, \[-5=\frac{1×0+2×a}{1+2}\text{ and }4=\frac{1×b+2×0}{1+2}\] \[-5=\frac{2a}{3}\text{ and }4=\frac{b}{3}\] \[\therefore a=\frac{-15}{2}\text{ and }b=12\]

Thus, equation of line is, \[\frac{x}{a}+\frac{y}{b}=1\] \[\frac{-2x}{15}+\frac{y}{12}=1\] \[-8x-5y=60\] \[\therefore 8x-5y+60=0\]

---

---