Point Slope Form and Two Points Form

Point slope form is used to find the equation of a line whose slope is given and which passes through a given point. Two points form is used to find the equation of a line passing through two given points.

Point Slope Form

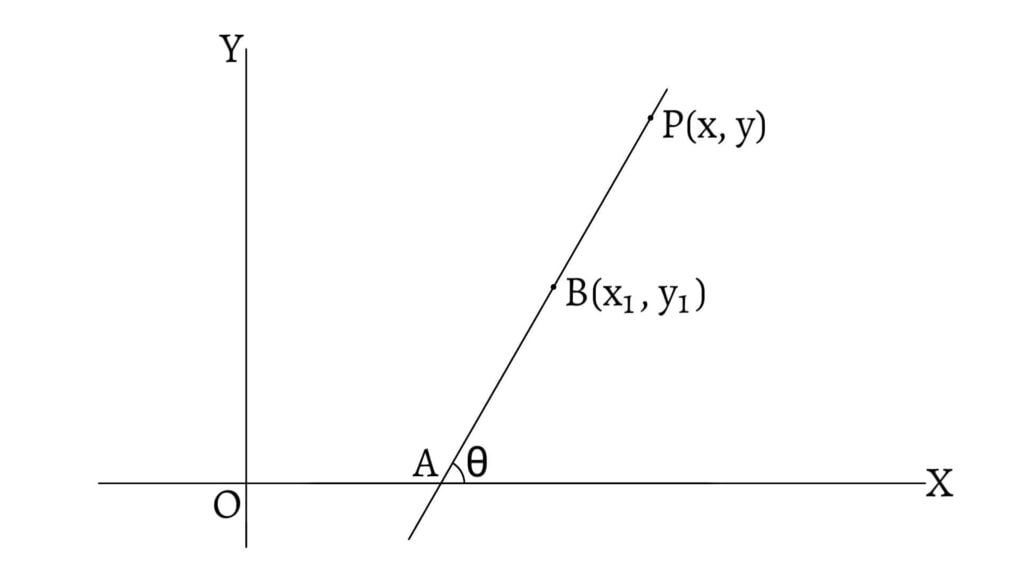
Let a straight line passing through a point $B(x_1,y_1)$ have its slope equal to $m=\tan\theta$. Let $P(x,y)$ be any point on the line. Then, \[\text{Slope of BP}=\frac{y-y_1}{x-x_1}\] \[\text{But, Slope of the line}=m\] \[\therefore \frac{y-y_1}{x-x_1}=m\] \[\therefore y-y_1=m(x-x_1)\] This is the required equation of the line which is known as point slope form.

Two Points Form

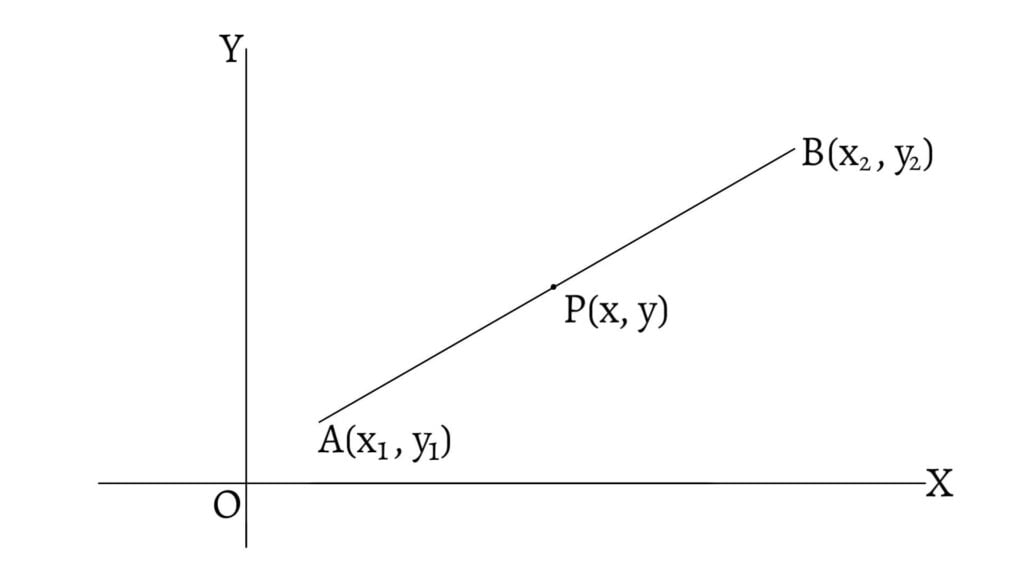
Let a straight line pass through the points $A(x_1,y_1)$ and $B(x_2,y_2)$. Let $P(x,y)$ be any point on the line. Then, \[\text{Slope of AP}=\frac{y-y_1}{x-x_1}\] \[\text{Slope of AB}=\frac{y_2-y_1}{x_2-x_1}\] Since $AP$ and $AB$ are the segments of the same straight line, their slopes are equal. \[\therefore \frac{y-y_1}{x-x_1}=\frac{y_2-y_1}{x_2-x_1}\] \[\therefore y-y_1=\frac{y_2-y_1}{x_2-x_1}(x-x_1)\] This is the required equation of the line which is known as two points form.

---

---