Circle
Consider a fixed point. Then, a circle is a closed curve around the point such that every point on the curve is at a constant distance from that point. In terms of locus, a circle may be defined as the locus of a point which moves so that its distance from a fixed point is constant.
The fixed point is called the centre and the constant distance is called the radius of the circle.
Equation of a Circle
Centre at the origin (Standard form)
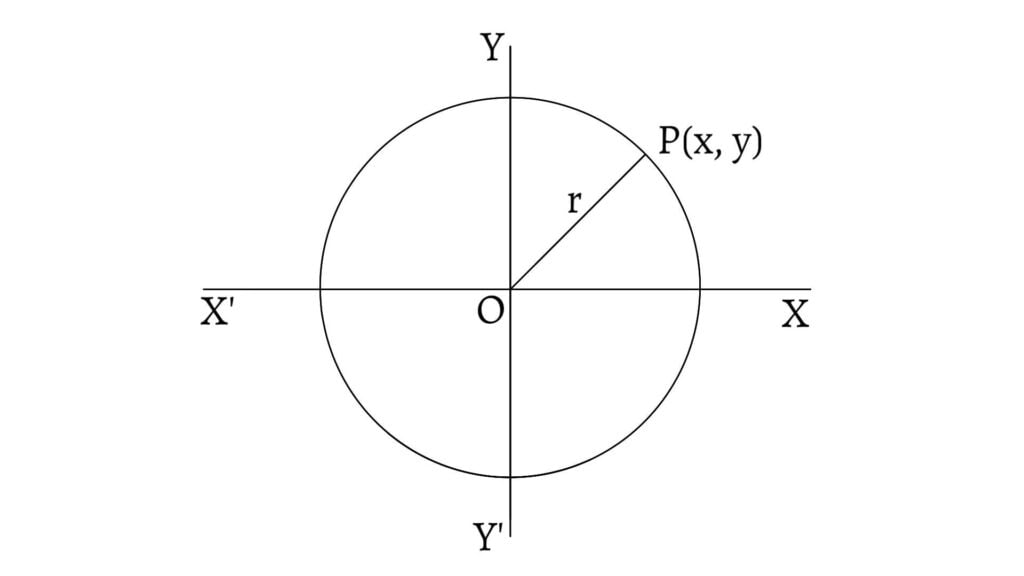
Let $O(0,0)$ be the centre and $r$ be the radius of the circle. Let $P(x,y)$ be any point on the circle. Then, \[OP=r\] \[\text{or, }OP^2=r^2\] \[\therefore x^2+y^2=r^2\] This relation is true for any point $P(x,y)$ on the circle. Hence it is the equation of the circle.
Centre at any point (Central form)

Let $C(h,k)$ be the centre and $r$ be the radius of the circle. Let $P(x,y)$ be any point on the circle. Then, \[CP=r\] \[\text{or, }CP^2=r^2\] \[\therefore (x-h)^2+(y-k)^2=r^2\] This is the equation of the circle. This relation can be used to find the equation of the circle for the following particular cases.
Equation of the circle touching the x-axis

Let $(h,k)$ be the centre of the circle. If the circle touches the x-axis, then the radius of the circle $(r)=k$. Hence, the equation of the circle touching the x-axis is \[(x-h)^2+(y-k)^2=k^2\]
Equation of the circle touching the y-axis

Let $(h,k)$ be the centre of the circle. If the circle touches the y-axis, then the radius of the circle $(r)=h$. Hence, the equation of the circle touching the y-axis is \[(x-h)^2+(y-k)^2=h^2\]
Equation of the circle touching both axes

Let $(h,k)$ be the centre of the circle. If the circle touches both axes, then the radius of the circle $(r)=h=k$. Hence, the equation of the circle touching both axes is \[(x-h)^2+(y-h)^2=h^2\]
General equation of the circle
Consider an equation \[x^2+y^2+2gx+2fy+c=0\] in which the coefficients of $x^2$ and $y^2$ are equal, each being unity and there is no term containing $xy$. The given equation may be written as \[x^2+y^2+2gx+2fy=-c\] \[x^2+2gx+g^2+y^2+2fy+f^2=g^2+f^2-c\] \[(x+g)^2+(y+f)^2=\left(\sqrt{g^2+f^2-c}\right)^2\text{ __(1)}\] which is in the form of $(x-h)^2+(y-k)^2=r^2$, hence these equation represents a circle. The equation of a circle in this form is called the general equation of the circle.
Comparing equation $\text{(1)}$ with the equation of a circle \[(x-h)^2+(y-k)^2=r^2\] we have $h=-g$, $k=-f$ and $r=\sqrt{g^2+f^2-c}$. Hence, the equation $x^2+y^2+2gx+2fy+c=0$ represents a circle whose centre is at $(-g,-f)$ and radius equal to $\sqrt{g^2+f^2-c}$.
- If $g^2+f^2-c>0$, the radius is real, hence the equation gives a real geometric locus.
- If $g^2+f^2-c=0$, the radius is zero. In this case, the circle is called a point circle.
- If $g^2+f^2-c<0$, the radius is imaginary. In this case, we say that the equation represents a circle with a real centre and an imaginary radius.
The general equation of second degree \[ax^2+2hxy+by^2+2gx+2fy+c=0\] represents a circle if $a=b$ (coefficients of $x^2$ and $y^2$ are equal) and $h=0$ (coefficient of $xy$ is zero).
Circle with a given diameter (Diameter form)
Let $A(x_1,y_1)$ and $B(x_2,y_2)$ be the ends of a diameter of a circle. Let $P(x,y)$ be any point on the circle. Join $AP$, $BP$ and $AB$. Since $AB$ is a diameter of the circle, $\angle APB$ is a right angle.

\[\text{Slope of AP}=\frac{y-y_1}{x-x_1}\] \[\text{Slope of BP}=\frac{y-y_2}{x-x_2}\] Since $AP\perp BP$, the product of their slopes is $-1$. \[\therefore\frac{y-y_1}{x-x_1}.\frac{y-y_2}{x-x_2}=1\] \[\text{or, }(x-x_1)(x-x_2)+(y-y_1)(y-y_2)=0\] This equation is satisfied by any points of the diameter of the circle. Hence, it is the equation of the circle.
Next: A Point, a Line and a Circle
