The Sine Law

The sine law of trigonometry states that;

1. The area of any triangle is half the product of any two sides and the sine of the angle between them. \[\Delta=\frac{1}{2}bc\sin A=\frac{1}{2}ca\sin B=\frac{1}{2}ab\sin C\]
2. The sides of a triangle are proportional to the sines of the opposite angles. \[\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}\]

Let $ABC$ be a triangle placed in the standard position with the vertex $A$ at the origin and the side $AB$ along the positive x-axis. Let us denote the angle $BAC$, $CBA$, $ACB$ of the triangle $ABC$ by $A$, $B$, $C$ respectively; and the lengths of the sides $BC$, $CA$, $AB$ by $a$, $b$, $c$ respectively.

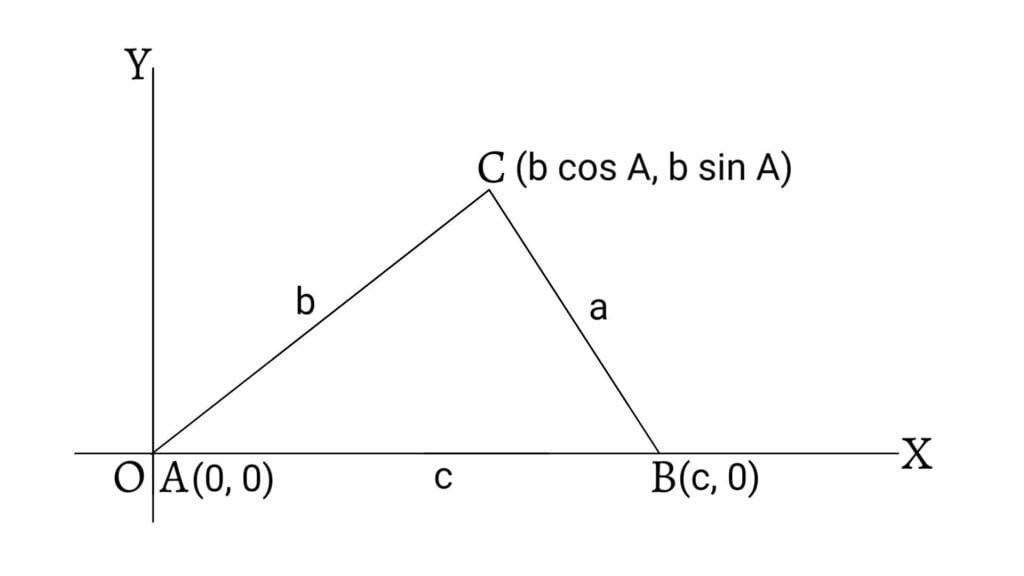
The coordinates of $A$, $B$ and $C$ are respectively $(0,0)$ $(c,0)$ and $(b\cos A, b\sin A)$. Now, the area of the triangle $ABC$ is given by,

\[\Delta ABC=\frac{1}{2}\text{base}×\text{altitude}\] \[=\frac{1}{2}AB×\text{ordinate of }C\] \[=\frac{1}{2}c×b\sin A\] \[=\frac{1}{2}bc\sin A\]

If the vertex $C$ is below the x-axis, then its coordinates will be $(b\cos A, -b\sin A)$. Hence, the area of the triangle will be, \[\Delta=-\frac{1}{2}bc\sin A\] Since, the area of the triangle is a positive quantity, for all the cases, \[\Delta=\frac{1}{2}bc\sin A\]

Similarly, placing the other angles $B$ and $C$ in the standard position, we can prove that \[\Delta=\frac{1}{2}ca\sin B\;\;\;\text{and}\;\;\;\Delta=\frac{1}{2}ab\sin C\]

Combining all these, we get, \[\Delta=\frac{1}{2}bc\sin A=\frac{1}{2}ca\sin B=\frac{1}{2}ab\sin C\]

Hence, we have, \[bc\sin A=ca\sin B=ab\sin C\] \[\Rightarrow \frac{bc\sin A}{abc}=\frac{ca\sin B}{abc}=\frac{ab\sin C}{abc}\] \[\Rightarrow \frac{\sin A}{a}=\frac{\sin B}{b}=\frac{\sin C}{c}\] \[\therefore \frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}\] This is the famous sine law of trigonometry.

[Also see: Vector Method to Prove the Sine Law]

Now, we shall give the second proof of the sine laws which will also give us the relations connecting the circum-radius $R$ with the sine of an angle and its opposite side.

Let $O$ be the circum-centre of a $\Delta ABC$. Join $BO$ and produce upto $D$. Join $DC$.

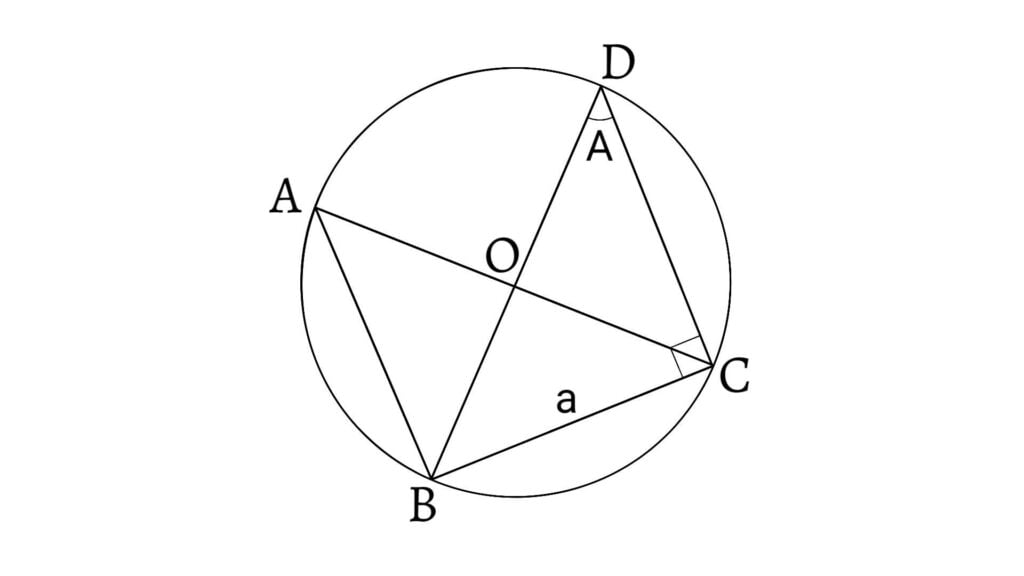
Then, \[\text{Circum-radius}=OB=OD=R\] \[\therefore BD=2R\] Now, \[\sin A=\frac{BC}{BD}=\frac{a}{2R}\] \[\therefore\frac{a}{\sin A}=2R\] Similarly, we can have \[\frac{b}{\sin B}=2R\;\;\;\text{and}\;\;\;\frac{c}{\sin C}=2R\] From above relations, \[\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R\]

---

Next: The Cosine Law

---