AC Through Circuit Elements

---

AC Through a Resistor

An AC source of emf $E$ and frequency $f$ is connected to a pure resistor of resistance $R$ as shown in figure.

The instantaneous emf across the resistor is given by \[E=E_0\sin\omega t\text{ __(1)}\]

where, $\omega=2πf$, $f$ being the frequency of the source and $E_0$ is its maximum emf.

Let $I$ be the instantaneous current in the circuit at any time $t$, then,

\[I=\frac{E}{R}=\frac{E_0}{R}\sin\omega t\] \[\therefore I=I_0\sin\omega t\text{ __(2)}\]

where, $I_0=\frac{E_0}{R}$ is the peak value of ac.

From $\text{(1)}$ and $\text{(2)}$, we find that current and voltage are in same phase. Hence, in an ac circuit containing only resistor, the current and voltage are in same phase as shown in the figure given below.

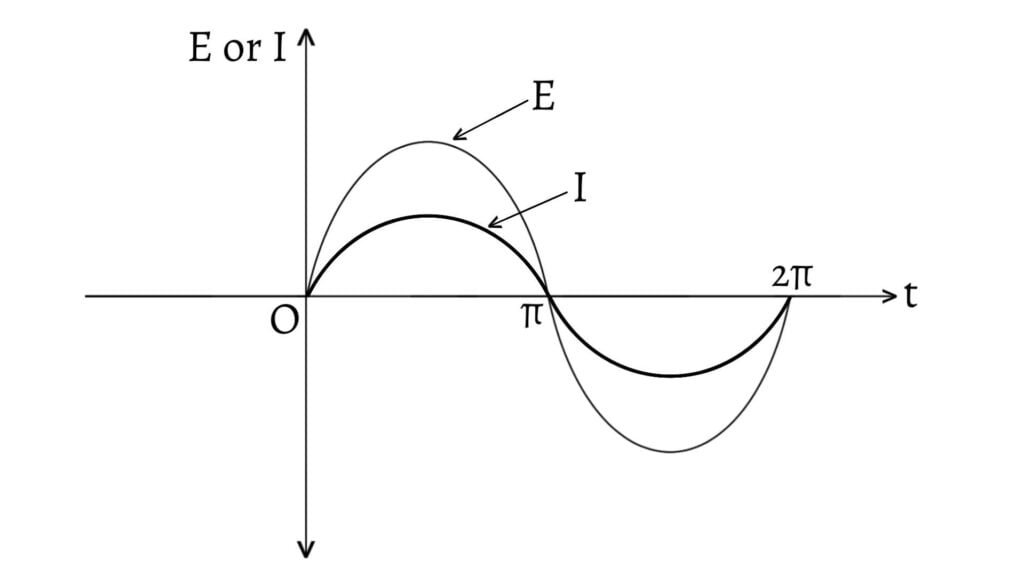
The phasor diagram or vector diagram showing the relationship between alternating current and alternating emf in an ac circuit containing only resistor is shown below.

AC Through an Inductor

An AC source of emf $E$ and frequency $f$ is connected to a pure inductor of inductance $L$ as shown in figure.

The instantaneous emf across the inductor is given by \[E=E_0\sin\omega t\text{ __(a)}\]

According to the Faraday’s laws of electromagnetic induction, an emf $(\varepsilon)$ is induced across the inductor given by \[\varepsilon=-L\frac{dI}{dt}\]

As there is no potential drop in the circuit, using Kirchhoff’s voltage law $(\sum V=\sum IR)$, the net emf in the circuit is given by \[E+\varepsilon=0\] \[E=L\frac{dI}{dt}\] \[E_0\sin\omega t\: dt=L\:dI\]

Integrating both sides, we get \[\int E_0\sin\omega t\:dt=\int L\:dI\] \[-\frac{E_0\cos\omega t}{\omega}=LI+C\text{ __(b)}\] where $C$ is an arbitrary constant.

For $I=0$, $\omega t=\frac{π}{2}$, Hence, \[-\frac{E_0\cos\frac{π}{2}}{\omega}=L×0+C\] \[\therefore C=0\]

Putting the value of $C$ in equation $\text{(b)}$, \[-\frac{E_0\cos\omega t}{\omega}=LI\] \[I=\frac{E_0}{\omega L}\sin\left(\omega t-\frac{π}{2}\right)\]

We have, inductive reactance $(X_L)$$=\omega L$. \[\therefore I=\frac{E_0}{X_L}\sin\left(\omega t-\frac{π}{2}\right)\] \[\therefore I=I_0\sin\left(\omega t-\frac{π}{2}\right)\]

where, $I_0=\frac{E_0}{X_L}$ is the peak value of ac.

Comparing $\text{(a)}$ and $\text{(c)}$, we find that current $I$ lags behind voltage $E$ by a phase angle of $\frac{π}{2}$. Conversely, the voltage $E$ leads the current $I$ by a phase angle of $\frac{π}{2}$.

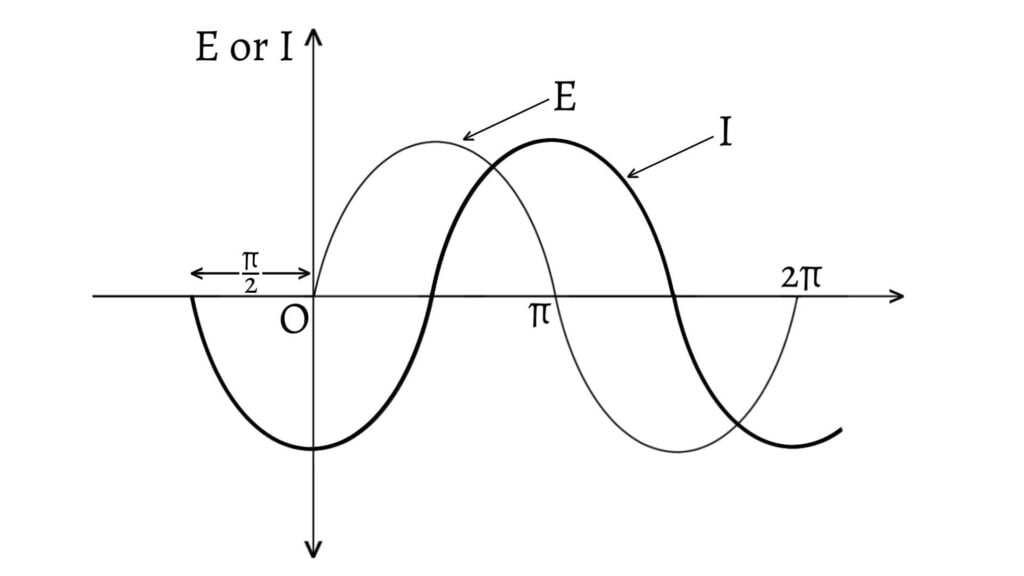
The phasor diagram or vector diagram of an ac circuit containing only an inductor is shown below.

AC Through a Capacitor

An AC source of emf $E$ and frequency $f$ is connected to a pure capacitor of capacitance $C$ as shown in figure.

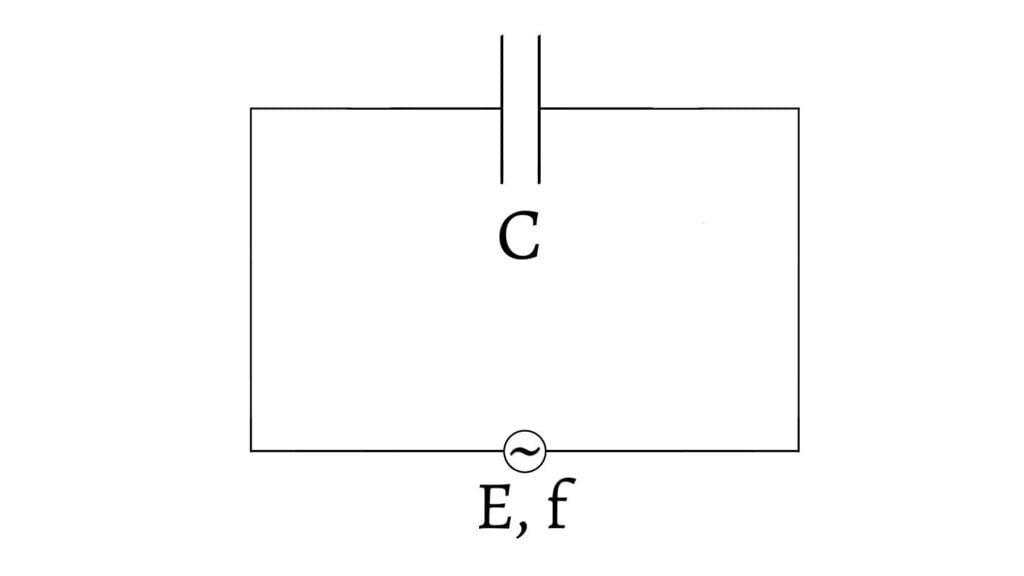
The instantaneous emf across the resistor is given by \[E=E_0\sin\omega t\text{ __(i)}\]

Let $q$ be the charge on the capacitor at any instant. Then, we can write \[q=CE\] \[q=CE_0\sin\omega t\]

The instantaneous current $(I)$ is given by \[I=\frac{dq}{dt}\] \[=\frac{d}{dt}(CE_0\sin\omega t)\] \[=\omega CE_0\cos\omega t\] \[=\omega CE_0\sin\left(\omega t+\frac{π}{2}\right)\]

We have, capacitive reactance $(X_C)$$=\frac{1}{\omega C}$. \[\therefore I=\frac{1}{X_C}E_0\sin\left(\omega t+\frac{π}{2}\right)\] \[\therefore I=I_0\sin\left(\omega t+\frac{π}{2}\right)\text{ __(ii)}\]

where, $I_0=\frac{E_0}{X_C}$ is the peak value of ac.

Comparing $\text{(i)}$ and $\text{(ii)}$, we find that current $I$ leads voltage $E$ by a phase angle of $\frac{π}{2}$. Conversely, the voltage $E$ lags behind the current $I$ by a phase angle of $\frac{π}{2}$.

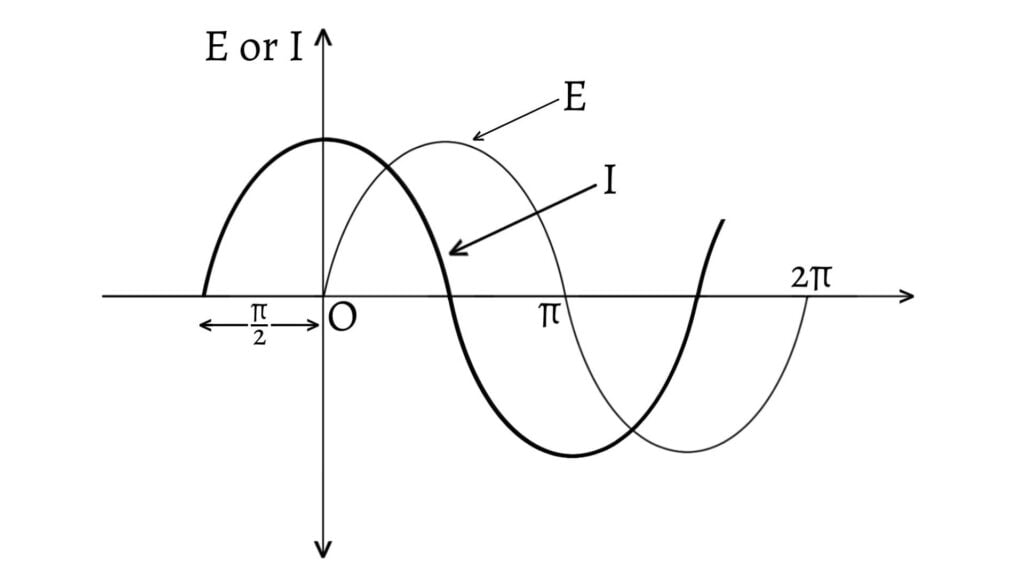
The phasor diagram or vector diagram of an ac circuit containing only a capacitor is shown below.

---

---