Transformer is an electric device which is used to convert low alternating voltage at high current into high alternating voltage at low current and vice versa. [Alternating Current and emf]
The circuit symbol of transformer is shown in the figure given below.
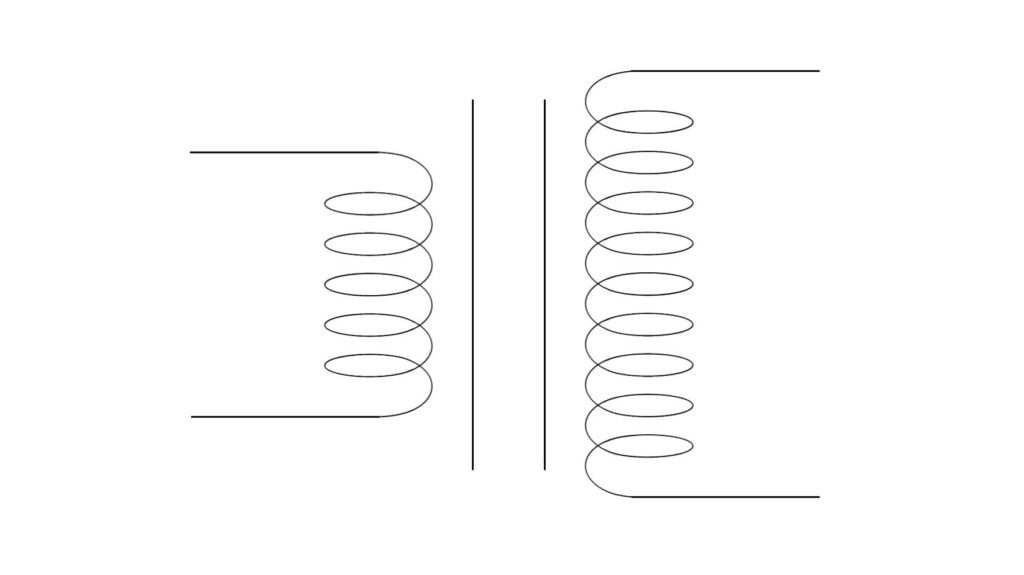
Types of Transformers
There are two types of transformers. They are:
Step up transformer
The transformer which converts low alternating voltage at high current into high alternating voltage at low current is called step up transformer. A step up transformer gives increased alternating output voltage. In this transformer, the number of turns in the secondary coil $(N_s)$ is greater than the number of turns in the primary coil $(N_p)$ i.e. $N_p<N_s$.
Step down transformer
The transformer which converts high alternating voltage at low current into low alternating voltage at high current is called step down transformer. A step down transformer gives decreased alternating output voltage. In this transformer, the number of turns in the primary coil $(N_p)$ is greater than the number of turns in the secondary coil $(N_s)$ i.e. $N_p>N_s$.
Principle
It is based on the principle of mutual induction i.e. when there is change in the current or magnetic flux of the primary coil, magnetic flux linked with the secondary coil changes and hence an emf is induced in the secondary coil.
Construction
Transformer consists of two windings or coils electrically insulated from each other and wound upon common laminated soft iron core made up of thin sheets. The thin rectangular sheets of soft iron (or silicon steel) are placed one above other. These plates are insulated from each other by painting or varnishing the consecutive sheets. In this way, we get a rectangular frame called a laminated core.

The coil connected to ac source is called primary coil and the coil connected to load is called secondary coil. The relative number of turns in the two coils depends upon whether it is required to transform up or down the ac voltage. The primary coil along with a source of alternating voltage is called primary circuit and the secondary coil along with load is called secondary circuit.
Soft iron (or silicon steel) is the ferromagnetic substance which has high permeability so it concentrates the magnetic lines of force and reduces the loss of energy. The lamination of the core prevents the formation of eddy currents. The two sets of coils are wound on a soft iron core on separate limbs of the core.
Working and Theory
When an ac source is connected to the primary coil, the magnetic flux linked with the primary coil and hence with the secondary coil changes. Due to self induction, an emf $(\varepsilon_p)$ is induced in the primary coil and due to mutual induction, an alternating emf $(\varepsilon_p)$ is induced in the secondary coil.
A transformer operates only on ac because if the primary coil is connected to a dc supply then there will be no changing flux in the primary coil and therefore no emf is induced in the secondary coil and hence it does not work.
Let $\frac{d\phi}{dt}$ be the rate of change of magnetic flux. This rate $\frac{d\phi}{dt}$ is same for both primary and secondary coils because the iron core is capable of coupling the whole of the magnetic flux $\phi$ produced by the turns of the primary coil with the secondary coil. It is assumed that there is no leakage of magnetic lines of force (magnetic flux) out of the iron core.
Let $N_p$ and $N_s$ be the number of turns in the primary coil and the secondary coil respectively. From Faraday’s laws of electromagnetic induction, the induced emf in the primary coil is given by \[\varepsilon_p=-N_p\frac{d\phi}{dt}\text{ __(1)}\] and, the induced emf in the secondary coil is given by \[\varepsilon_s=-N_s\frac{d\phi}{dt}\text{ __(2)}\] Dividing $\text{(2)}$ by $\text{(1)}$, we get \[\frac{\varepsilon_s}{\varepsilon_p}=\frac{N_s}{N_p}\text{ __(3)}\] This relation is called transformer equation.
The equation $\text{(3)}$ can also be written as \[\frac{\varepsilon_p}{N_p}=\frac{\varepsilon_s}{N_s}\]
Hence, emf induced per unit turn is the same in primary as well as in secondary coil.
Here, \[\frac{N_s}{N_p}=\sqrt{\frac{L_s}{L_p}}=K\] where, $L_p$ and $L_s$ are the coefficients of self induction of primary and secondary coils respectively. This ration $\frac{N_s}{N_p}$ is called transformation ratio $(K)$.
Let $I_p$ and $I_s$ be the currents in the primary coil and secondary coil respectively. Then \[\text{Input power}=\varepsilon_p I_p\] \[\text{Output power}=\varepsilon_s I_s\]
An ideal transformer is a transformer that has no winding resistance and no leakage flux i.e. the same flux links both the windings and there is no iron loss in the core. Hence for an ideal transformer, there is no loss of power and hence we can write
\[\text{Input power}=\text{Output power}\] \[\varepsilon_p I_p=\varepsilon_s I_s\] \[\therefore\frac{\varepsilon_s}{\varepsilon_p}=\frac{I_p}{I_s}=K\]
Hence, in general, \[\varepsilon∝\frac{1}{I}\]
From this relation, it is clear that for a step up transformer, $\varepsilon_s>\varepsilon_p$ so $I_s<I_p$ i.e. secondary current is low when secondary voltage is high. Hence, whatever we gain in voltage, we lose in current in the same ratio. Similarly, for a step down transformer, whatever we lose in voltage, we gain in current in the same ratio.
Thus, a step up transformer increases the alternating voltage by decreasing the alternating current and a step down transformer decreases the alternating voltage by increasing the alternating current. The output signal has the same frequency as the input signal. It means that ac voltage and current change but frequency remains same in a transformer.
Efficiency of a Transformer
The efficiency of a transformer is defined as the ratio of output power to the input power. \[\text{Efficiency }(\eta)=\frac{\text{Output power}}{\text{Input power}}=\frac{\varepsilon_s I_s}{\varepsilon_p I_p}\]
For an ideal transformer, efficiency is $100\%$ but efficiency of a real transformer is not $100\%$ due to loss of energy. The efficiency of a transformer varies from $90-99\%$.
Energy Losses in a Transformer
Copper Loss
Primary and secondary coils of a transformer are generally made up of copper wires. These copper wires have resistance $R$, and according to the Joule’s law of heating, if current $I$ flows through the wire then $I^2R$ amount of heat is produced. Hence, power loss of $I^2R$ takes place. This loss of energy in the form of heat is known as copper loss. Copper loss can be reduced by using thick wires for windings.
Iron Losses:
a) Eddy Current Loss
Due to the change in magnetic flux linked with the iron core, eddy currents are set up. These eddy currents produce heat which leads to the loss of energy. It is minimised by using a laminated iron core.
b) Hysteresis Loss
When ac passes the primary coil, the iron core gets magnetized and demagnetized over a complete cycle. Due to the repeated magnetization and demagnetization of the iron core, there is loss of energy which is equal to the area of the hysteresis loop. This loss of energy can be minimised by using suitable material having narrow hysteresis loop such as silicon iron core.
Flux Linkage Loss
In an actual transformer, the coupling between the primary coil and the secondary coil is not same. It means that the magnetic flux linked with the primary coil is not equal to the magnetic flux linked with the secondary coil. Hence, magnetic flux is not confined entirely to the iron core. Some of the flux lines return through air. The leakage of magnetic flux takes place in both primary and secondary coils which causes loss in the magnetic energy. This loss is called flux linkage loss.
Loss due to vibration of core
Due to magnetostriction, vibration is produced in the core. Hence, some electrical energy is lost in the form of mechanical energy to produce vibration.
Uses of a Transformer
A transformer is used in almost all ac operations. It is used in voltage regulator for almost all ac appliances like TV, computer, refrigerator, etc. A step down transformer is used for welding purposes. It is mainly used in transmission of ac over a long distance to minimise the power loss.
Previous: Eddy Current
