Here, we will discuss about the different cases and analyse the motion of a body in a vertical circle.
Suppose a body of mass $m$ is tied at the end of a string. Let the body be moving in a vertical circle with constant speed $v$. Let the radius of the circle be $r$ which is the length of the string. Let $P$ be any point on the circle at angle $θ$ from mean position. Consider four positions $A$, $B$, $C$ and $D$ on the circle. $A$ is the lowest point and $C$ is the highest point. Different components of force at $P$ are shown in figure given below.
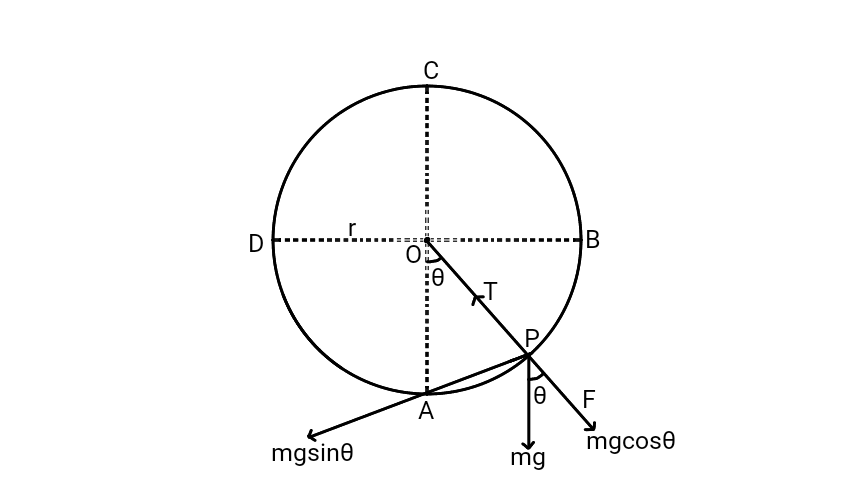
Let $F$ be the centripetal force, $T$ be the tension in the string which always acts towards the point $O$ and $mg$ is the weight of the body which always acts downward. From the figure, it is clear that the tension in the string is balanced by $mg\cos θ$ and the centripetal force of the body. \[T = F + mg\cos θ\] \[T = \frac{mv^2}{r} + mg\cos θ\]
Maximum Tension in the String

At the lowest point $A$, tension $T$ acts upward while the weight of the body acts downward. So, tension is maximum in the string at this point. \[\text{At point A, }θ=0°,\] \[T_{\text{max}} = \frac{mv^2}{r} + mg\cos 0\] \[T_{\text{max}} = \frac{mv^2}{r} + mg\]
Minimum Tension in the String

At highest point $C$, tension $T$ and weight $mg$ both acts downward. So, tension in the string at this point is minimum. \[\text{At point C, }θ=180°,\] \[T_{\text{min}} = \frac{mv^2}{r} + mg\cos 180\] \[T_{\text{min}} = \frac{mv^2}{r} – mg\]
Tension in the String at B and D
\[\text{At point B or D, }θ=90°,\] \[T = \frac{mv^2}{r} + mg\cos 90\] \[T = \frac{mv^2}{r}\]
Minimum Velocity required to Loop in the Vertical Circle
At highest point $C$, tension is minimum. If the tension is zero at this point, then the weight of the body provides necessary centripetal force to loop in a vertical circle. \[0+mg=\frac{mv_{\text{min}}^2}{r}\] \[mg=\frac{mv_{\text{min}}^2}{r}\] \[v_{\text{min}}^2=gr\] \[v_{\text{min}}=\sqrt{gr}\] This is the minimum velocity also called as critical velocity required at the top so that the string does not slack.
At lowest point $A$, tension is maximum. According to the principle of conservation of energy, \[\text{K.E. of body at A}=\text{(K.E.+P.E.) of the body at C}\] \[\frac{1}{2}mv^2=\frac{1}{2}mv_{\text{min}}^2+mg(2r)\] \[\frac{1}{2}v^2=\frac{1}{2}v_{\text{min}}^2+2gr\] \[v^2=v_{\text{min}}^2+4gr\] \[\text{Here, }v_{\text{min}}^2=gr\] \[v^2=gr+4gr\] \[v=\sqrt{5gr}\] Hence, the velocity must be equal to or greater than $\sqrt{5gr}$ for the body to move in a vertical circle.
- If a bucket containing water is rotated along a vertical circle such that its velocity at the lowest point is equal to or greater than $\sqrt{5gr}$, the water will not spill, even at the highest point.
- The pilot of a jet plane who is not tied to his seat will not fall down while looping the vertical circle.
- For the same reason, in circus, the motorcyclists are able to move in a vertical circle inside a cage.
More on Circular Motion
