Angle of Friction
Angle of friction is defined as the angle made by the resultant of normal reaction and frictional force with the normal reaction.
Consider a body lying on a horizontal surface. Let $R$ be the normal reaction and $F_c$ be the frictional force. If $\alpha$ is the angle made by the resultant of normal reaction and frictional force with the normal reaction, then, $\alpha$ is the angle of friction.
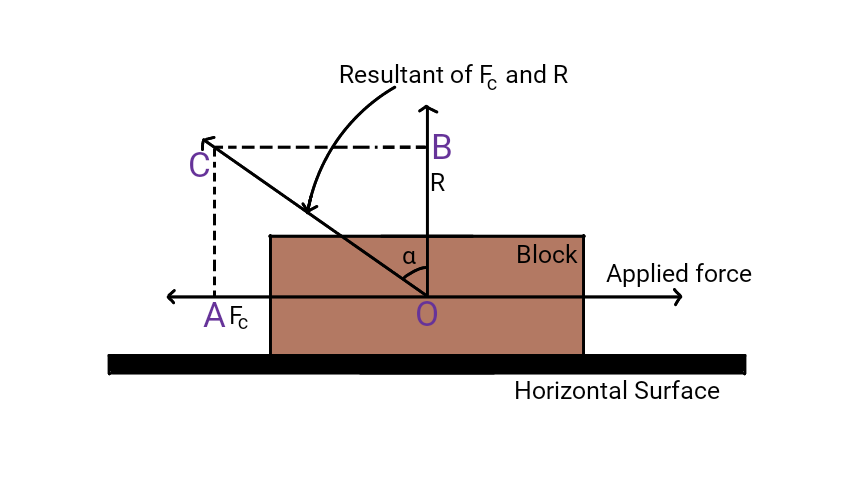
Here, \[\tan\alpha = \frac{BC}{OB}\] \[\tan\alpha = \frac{OA}{OB}\] \[\tan\alpha = \frac{F_c}{R}\] \[\therefore \tan\alpha=\mu\text{ ___(1)}\] Therefore, coefficient of limiting friction is equal to the tangent of angle of friction.
Angle of Repose
Angle of repose is defined as the angle of an inclined plane, at which a body placed on it just begins to slide.
Place a body of mass $m$ on an inclined plane. Increase the angle of inclined plane till the body just begins to slide. If $\theta$ is the angle of inclination at which the body just begins to slide, then $\theta$ is the angle of repose.
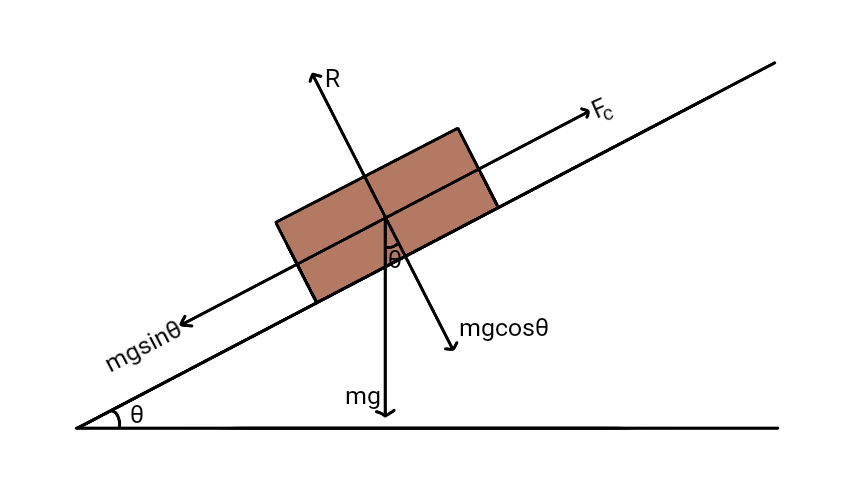
The weight $mg$ of the body acts vertically downwards. Because of the angle of inclination, this weight can be resolved into two components; $mg\cos\theta$ and $mg\sin\theta$ as shown in fig.
If the body just begins to slide, then
1. $mg\sin\theta$ is equal to the frictional force \[mg\sin\theta=F_c\text{ __(a)}\]
2. $mg\cos\theta$ is equal to the normal reaction \[mg\cos\theta=R\text{ __(b)}\]
Dividing $\text{(a)}$ by $\text{(b)}$, \[\frac{mg\sin\theta}{mg\cos\theta}=\frac{F_c}{R}\] \[\tan\theta=\frac{F_c}{R}\] \[\tan\theta=\mu\text{ ___(2)}\]
Thus, coefficient of limiting friction is equal to the tangent of the angle of repose.
Relation between Angle of Friction and Angle of Repose
From $\text{(1)}$ and $\text{(2)}$, \[\tan\alpha=\mu=\tan\theta\] \[\tan\alpha=\tan\theta\] \[\alpha=\theta\] Thus, angle of friction is equal to the angle of repose.
Previous: Friction
