Forces produce various effects on a material body. One of them is turning effect. This effect of the force comes into action many times in our daily life. Opening a door, turning a tap, operating a screw driver are some of these effects. This turning effect is known as moment of a force.
It has been observed that if we use long-handled screw driver to unscrew a nut rather than a short-handled, then we have to apply a very small force. These observations lead us to the fact that turning effect of force depends upon;
- the magnitude of the force
- the perpendicular distance of the line of action of the force from the point or axis about which the turning takes place.

The combined effect of these two factors is known as the moment of the force applied.
The moment of a force about a given point is the product of the magnitude of the force and the perpendicular distance of the point from the line of action of the force.
Let $F$ be the force and $p$ be the perpendicular distance of the point $O$ from $AB$ (line of action of the force $F$). Then, \[\text{Moment of F about O}=F×p\] The moment of $F$ about $O$ is zero if;
- $F=0$, i.e. the force itself is zero
- $p=0$ i.e. when the line of action of the force passes throught the point about which the moment is to be taken.
Geometrical Interpretation of Moment
Let a force $F$ be represented in magnitude and direction by $AB$ and $O$ be the point about which the moment is taken. Join $OA$ and $OB$. Draw $OD⊥AB$ or $AB$ produced.

Thus, the moment of the force $F$ about $O$, \[=F×OD\] \[=AB×OD\] \[=2×\frac{1}{2}×AB×OD\] \[=2∆OAB\]
Thus, the moment of the force $F$ about $O$ is represented numerically by twice the area of a triangle whose base is the line representing the force and vertex is the point about which the moment is taken.
Physical Meaning of Moment
Let a plane lamina can turn freely about a point $O$.
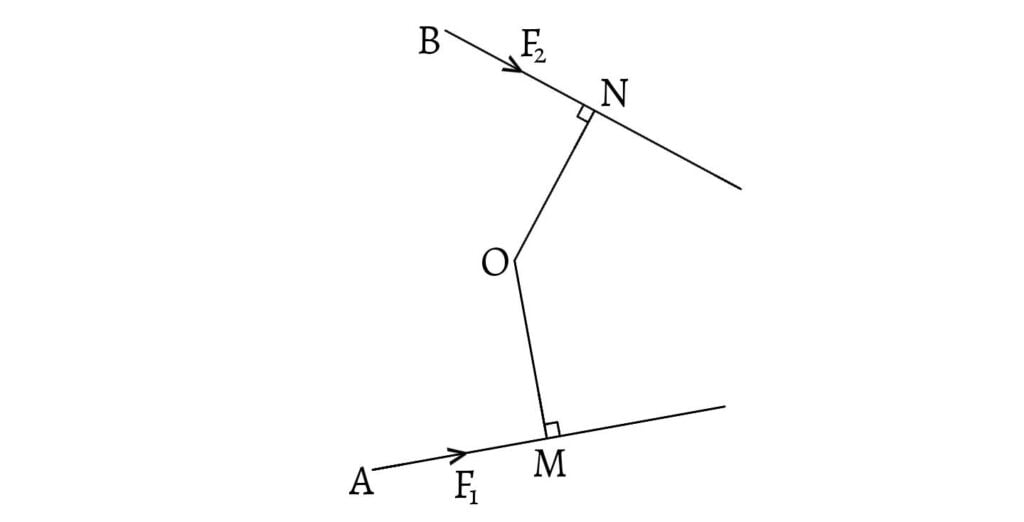
If a force $F_1$ is applied at $A$, then the force $F_1$ will make the body to turn about $O$ in anticlockwise direction. In the same way, if a force $F_2$ is applied at $B$, then the force $F_2$ will make the body to turn about $O$ in clockwise direction.
From $O$, draw $OM$ and $ON$ perpendicular to the line of action of the forces $F_1$ and $F_2$ at $M$ and $N$ respectively.
- If $F_1×OM=F_2×ON$, the body remains at rest.
- If $F_1×OM>F_2×OM$, the body turns about $O$ in anticlockwise direction.
- If $F_1×OM<F_2×OM$, the body turns about $O$ in clockwise direction.
Sign of the Moment
The force tends to turn the lamina clockwise or anticlockwise. Since these tendencies are opposite in nature, we have to distinguish between them by adopting sign convention. Thus, if the force tends to turn the body anticlockwise, the moment would be positive and if the force tends to turn the body clockwise, the moment would be negative.
Varignon’s Theorem
The algebraic sum of the moments of any two forces about any point in their plane is equal to the moment of their resultant about the same point.
Let $P$ and $Q$ be the two forces and let $R$ be their resultant.
Case I: When $P$ and $Q$ meet at a point
Let $AB$ represents the force $P$ and $AC$ represents the force $Q$ in magnitude and direction. Let $O$ be a point about which moments are to be taken. Through $O$, draw $OC//AB$ to meet the line of action of $Q$ at $C$. Complete the parallelogram $ABDC$. Then, $AD$ represents the resultant $R$. Join $OA$ and $OB$.

From both the figures, the moments of $P$, $Q$ and $R$ about $O$ are represented numerically by $2∆OAB$, $2∆OAC$ and $2∆OAD$ respectively.
In figure $(1)$, the moments of $P$ and $Q$ about $O$ are both positive, their algebraic sum is
\[2∆OAB+2∆OAC=2∆ADB+2∆OAC \text{ } (\because ∆OAB=∆ADB)\] \[=2∆ACD+2∆OAC\] \[=2∆OAD\] \[=\text{Moment of R about O}\]
In figure $(2)$, the moment of $P$ about $O$ is positive and the moment of $Q$ about $O$ is negative, their algebraic sum is
\[2∆OAB-2∆OAC=2∆ADB-2∆OAC\]\[=2∆ACD-2∆OAC\] \[=2∆OAD\] \[=\text{Moment of R about O}\]
Case II: When $P$ and $Q$ are parallel
Consider $P$ and $Q$ to be two parallel forces having $R$ as their resultant. Let $O$ be any point in their plane.

Through $O$, draw a line perpendicular to the lines of action of the forces $P$, $Q$ and $R$ to meet them in $A$, $B$ and $C$ respectively. Since the forces are parallel, \[R=P+Q\] \[P×AC=Q×BC \text{ __(1)}\]
In figure $(i)$, the algebraic sum of the moments of the forces $P$ and $Q$ about $O$
\[=P×OA+Q×BO\] \[=P(AC+OC)+Q(OC-BC)\] \[=P×AC+P×OC+Q×OC-Q×BC\] \[=P×OC+Q×OC \text{ } (\because P×AC=Q×BC)\] \[=(P+Q)OC\] \[=R×OC\] \[=\text{Moment of R about O}\]
In figure $(ii)$, the algebraic sum of the moments of the forces $P$ and $Q$ about $O$
\[=P×AO-Q×OB\] \[=P(AC+OC)-Q(BC-OC)\] \[=P×AC+P×OC-Q×BC+Q×OC\] \[=(P+Q)OC\] \[=R×OC\] \[=\text{Moment of R about O}\]
Varignon’s Generalised Theorem of Moments
If any number of coplanar forces acting on a rigid body have a resultant, then the algebraic sum of the moments about any point in their plane is equal to the moment of their resultant about the same point.
Let $O$ be a point in a plane about which moments are to be taken. Let $P_1, P_2, P_3, …$ be the number of forces acting in the plane.
Let $R_1$ be the resultant of $P_1$ and $P_2$, and $R_2$ be the resultant of $R_1$ and $P_3$. Then, $R_2$ is the resultant of $P_1$, $P_2$ and $P_3$. Similarly, let $R_3$ be the resultant of $R_2$ and $P_4$, then $R_3$ is the resultant of $P_1$, $P_2$, $P_3$ and $P_4$. In this way, we can find the resultant of all the forces.
Now, the algebraic sum of the moments of $P_1$ and $P_2$ about $O$ is equal to the moment of $R_1$ about $O$. Again, the algebraic sum of the moments of $R_1$ and $P_3$ i.e. $P_1$, $P_2$ and $P_3$ about $O$ is equal to the moment of $R_2$ about $O$ and so on till all the forces have been considered.
Hence, the algebraic sum of the moments of $P_1, P_2, P_3, …$ about $O$ is equal to the moment of their resultant about the same point.
Q. Masses of $1$ $\text{kg}$, $2$ $\text{kg}$, $3$ $\text{kg}$ and $4$ $\text{kg}$ are suspended from a uniform rod of length $5$ $\text{m}$, at a distance of $1$ $\text{m}$, $2$ $\text{m}$, $3$ $\text{m}$ and $4$ $\text{m}$ respectively from one end. If the mass of the rod is $4$ $\text{kg}$, find the position of the point about which it will balance.
Let $AB$ be the rod and $A$ be the end from which the given distances are measured. Let $O$ be the point about which moments are taken which is at $x$ distance from $A$.

Taking moments about $O$,
\[4(4-x)+3(3-x)=4\left(x-\frac{5}{2}\right)+2(x-2)+1(x-1)\] \[25-7x=7x-15\] \[14x=40\] \[x=\frac{20}{7} \text{ m}\]
Hence, the rod will balance about a point which is at a distance of $20/7$ $\text{m}$ from the end $A$.
Q. At what height from the base of a tree must the end of a rope be fixed so that a man on the ground, pulling at its other end with a given force, may have the greatest tendency to make the tree overturn?
Let $OA$ be the tree whose base is $O$. Let $BC$ be a rope of length $l$ fixed on the tree at a point $B$.
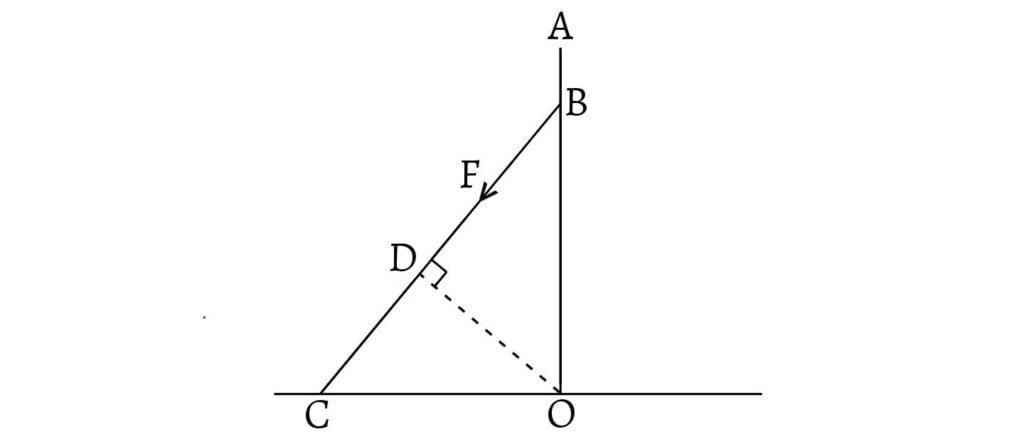
Let a man at $C$, on the ground pull the rope with the force $F$. From $O$, draw $OD⊥BC$. Let $OBC=θ$.
Then, moment of the force about $O$
\[=F×OD\] \[=F×OB\sin\theta\] \[=F×BC\cos\theta×\sin\theta\] \[=\frac{1}{2}F×l×2\sin\theta \cos\theta\] \[=\frac{1}{2}Fl\sin2\theta\]
For the moment to be greatest, \[\sin2\theta=1\] \[\therefore \theta=45°\] \[\text{Now, } OB=BC\sin45°=\frac{l}{\sqrt{2}}\]
Thus, the rope must be fixed at a height of $l/√2$ from the base of the tree.
More on Rotational Dynamics
- Torque and Couple
- Moment of Inertia and Radius of Gyration
- Angular Momentum and Rotational Kinetic Energy
