Torque
The turning effect of force is called moment of force or torque. It is the product of magnitude of force and the perpendicular distance of the line of action of force from the axis of rotation. It is denoted by $τ$.
Torque $=$ Force $×$ perpendicular distance from the axis of rotation.
If force $= F$ and perpendicular distance $= r$, then, \[τ=Fr\]
Its SI unit is $\text{Nm}$.
Relation Between Torque And Angular Acceleration
Consider a rigid body which has a particle of mass $m$ situated at distance $r$ from the axis of rotation. Suppose an external torque $τ$ is applied on the body which will produce an angular acceleration $α$ in the motion of the particle.
Then, \[τ=Fr\] \[τ=mar\] \[τ=mαr^2\]
This gives the torque for a single particle. But there are large number of particles in the body.
Suppose there are $n$ particles of masses $m_1, m_2, m_3, …, m_n$ situated at distances $r_1, r_2, r_3, …, r_n$ respectively from the axis of rotation. Then, the net torque is given by the total sum of the torque acting on each particles.
\[τ=τ_1+τ_2+τ_3+…+τ_n\]
\[τ=m_1r_1^2α+m_2r_2^2α+m_3r_3^2α+…+m_nr_n^2α\]
\[τ=(m_1r_1^2+m_2r_2^2+m_3r_3^2+…+m_nr_n^2)α\]
\[τ=\left(\sum_{i=1}^nm_ir_i^2\right)α\] \[∴τ=Iα\]
\[\sum_{i=1}^nm_ir_i^2=I\text{ (Moment of Inertia)}\] \[\text{If α=1, } I=τ\]
Therefore, moment of inertia of a rigid body about an axis of rotation is numerically equal to the external torque required to produce a unit angular acceleration in the rotational motion of the body about that axis.
In translation motion, an external force is required to produce change in the motion of body and is given by, \[F=ma\]
In rotational motion, an external torque is required to produce change in the motion of body and is given by, \[τ=Iα\]
Work Done By A Torque
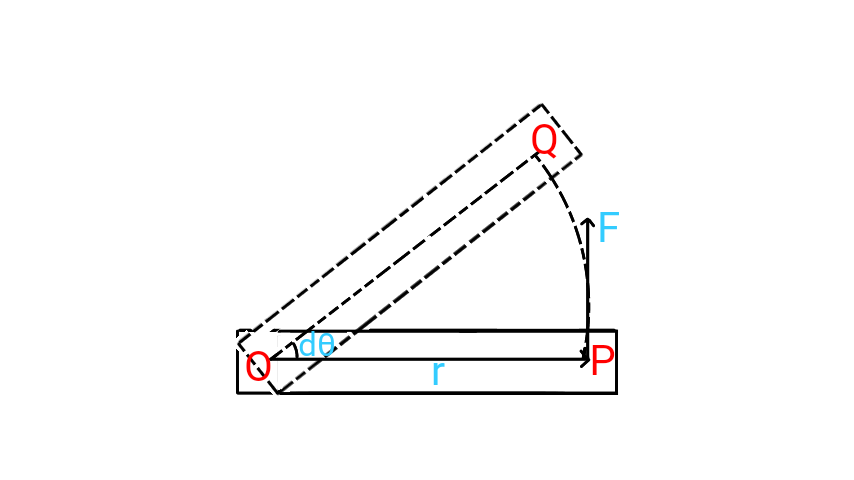
Consider a rigid body rotating about an axis passing through point $O$. Suppose on applying force $F$ at point $P$ such that $OP=r$, it rotates through infinitesimally small distance $dθ$. Since the distance moved is infinitesimally small, the distance moved $PQ$ can be approximately taken as linear. Therefore, small work done in moving the body from infinitesimally small distance $dθ$ is,
\[dW=F(PQ)\] \[dW=F(rdθ)\] \[dW=Frdθ\]
Here, \[Fr=\text{torque due to applied force (τ)}\] \[∴dW=τdθ\]
If the body is rotated through an angle $θ$, the total work done by the torque is given by, \[W=\int_0^θτ\;dθ\] \[W=τθ\]
If the body moves from $P$ to $Q$ in time $t$, then,
\[\text{Power}=\frac{τθ}{t}\] \[\text{Power}=τω\]
Couple
Two equal and opposite parallel forces acting on a rigid body at different points constitute a couple. Such a pair of forces acting upon a rigid body cannot produce a motion of translation but produce only rotation.
The perpendicular distance between the lines of the action of the two forces is known as the arm of the couple. The moment of a couple or torque is the product of the magnitude of one of the forces forming the couple and the arm of the couple.
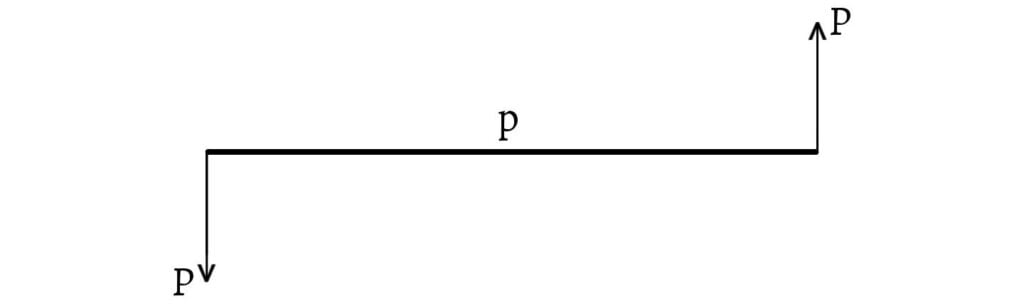
If $P$ is the magnitude of the forces and the arm of the couple is $p$, then the couple is denoted by $(P, p)$ and its moment is $P×p$. The moment of the couple is considered positive or negative according as the couple tends to rotate the body in anticlockwise or clockwise direction. The axis of the couple is a line perpendicular to the plane of the couple through any point in the plane and of length proportional to the moment of the couple.
The forces appied to the handle of screw driver, to the lid of a bottle while opening or closing it, to the key of a clock in winding it up or to the handle of the door while opening it are some examples of couple.

Let us consider a flywheel with radius $r$ rotating about its centre at $O$. Suppose two equal and opposite forces are applied tangentially at points $A$ and $B$ of a diameter of the wheel.
Let $θ$ be the angle of rotation of the wheel with force $F$ when the point $A$ is shifted to $A’$ and consequently $B$ to $B’$. Then, torque couple is,
\[τ_{\text{couple}}=F×2r=2Fr\]
Then, the work done due to angular displacement of wheel by $θ$ is,
\[W=W_1+W_2\]
\[W=Frθ+Frθ\]
\[W=2Frθ\]
\[W=τ_{\text{couple}}θ\]
Hence, work done by couple is the product of torque applied and angular displacement of rotational body.
Theorems of Couple
Theorem 1: The algebraic sum of the moments of two forces forming a couple about any point in their plane is constant and equal to the moment of the couple.
Let $(P, p)$ be a couple and $O$ be any point in the plane of the forces. Through $O$, draw a line perpendicular to the lines of action of the forces meeting them at $A$ and $B$.
Case I:
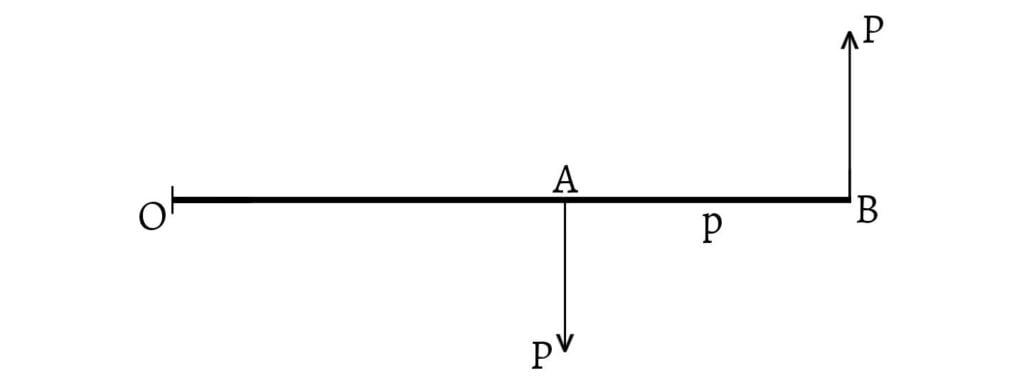
The algebraic sum of the moments of the forces about $O$
\[=P×OB-P×OA\] \[=P(OB-OA)\] \[=P×AB\] \[=P×p\] \[=\text{Moment of the couple}\]
Case II:
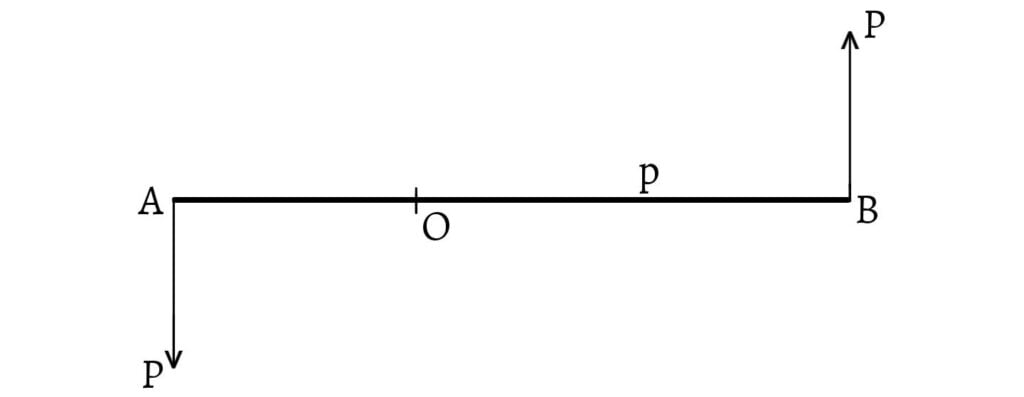
The algebraic sum of the moments of the forces about $O$
\[=P×OA+P×OB\] \[=P(OA+OB)\] \[=P×AB\] \[=P×p\] \[=\text{Moment of the couple}\]
Case III:

The algebraic sum of the moments of the forces about $O$
\[=P×OA-P×OB\] \[=P(OA-OB)\] \[=P×AB\] \[=P×p\] \[=\text{Moment of the couple}\]
Hence, in every cases, the algebraic sum of the moments is constant and equal to the moment of the couple wherever maybe the point $O$ is taken in the plane of the forces.
Theorem 2: Two couples, acting in the same plane upon a rigid body, whose moments are equal in magnitude but opposite in sign, balance one another.
Let $(P, p)$ and $(Q, q)$ be the given couples, then, \[P×p=Q×q\]
Case I: When the forces forming the couples are not parallel

Let one of the forces $P$ of one of the couples intersect one of the forces $Q$ of the other couple at $O$. Let the other two forces intersect at $O’$.
Draw $OM⊥O’P$ and $ON⊥O’Q$ so that
\[OM=p \;\;\; \text{and} \;\;\; ON=q\]
The two forces $P$ and $Q$ at $O$ are respectively equal and opposite to the forces at $O’$. Since both of the pairs act at the same angle, their resultants must be equal in magnitude but opposite in sign i.e. the resultant of the two forces $P$ and $Q$ at $O$ acts along $OO’$ and the resultant of the two forces $P$ and $Q$ at $O’$ acts along $O’O$. Hence, they cancel each other.
The sum of the moments of $P$ and $Q$ acting at $O’$ about $O$
\[=P×p-Q×q=0\]
Thus, the resultant of the forces forming the two couples vanish and hence the couples balance one another.
Case II: When the forces forming the couples are parallel

Draw a straight line perpendicular to the lines of action of the forces, meeting them at $A$, $B$, $C$ and $D$.
Since the moments of the couples are equal in magnitude,
\[P×AB=Q×CD \text{ ____(1)}\]
Let the resultant $P+Q$ of the like parallel forces $P$ at $B$ and $Q$ at $C$ act at a point $O$, then,
\[P×BO=Q×CO \text{ ____(2)}\]
Subtracting $(2)$ from $(1)$,
\[P(AB-BO)=Q(CD-CO)\] \[P×AO=Q×DO\]
Thus, the resultant $P+Q$ of the like parallel forces $P$ at $A$ and $Q$ at $D$ also acts at the same point $O$. Since these two resultants are equal in magnitude but opposite in directions and act at the same point, they are in equilibrium and hence, the two couples balance one another.
Cor. Two couples in the same plane, having equal moments are equivalent to one another.
Theorem 3: The effect of a couple upon a rigid body is unaltered if it is transferred to any plane parallel to its own.
Let $AB$ be the arm of a couple $(P, p)$. Now, move the couple so that the arm occupies the position $CD$ in a parallel plane. Join $AD$ and $BC$. Let the point of intersection be $O$. Since $AB$ and $CD$ are equal and parallel, $O$ is the middle point of both $AD$ and $BC$.
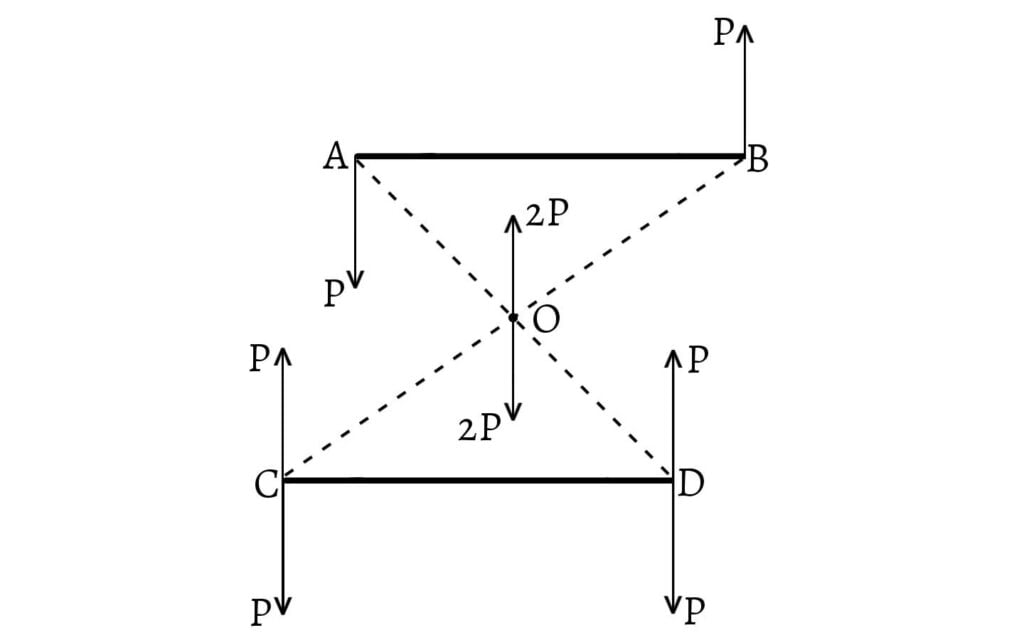
At $C$ and $D$, let two equal and opposite forces act, each being equal and parallel to $P$. Now, like parallel forces $P$ at $A$ and $P$ at $D$ have a resultant force $2P$ at $O$. Similarly, like parallel forces $P$ at $C$ and $P$ at $B$ have a resultant force $2P$ at $O$ which is in the direction opposite to that of the resultant of the forces at $A$ and $D$. These two resultants balance each other. Now, the two unlike parallel forces $P$ at $C$ and $P$ at $D$ are left, which form a couple equivalent to the original one. Also, the plane of the new couple is parallel to that of the original couple.
Cor. A couple may be replaced by any other couple acting in a parallel plane, provided the moments of the two couples are the same.
Theorem 4: Any number of couples in the same plane acting on a rigid body are equivalent to a single couple whose moment is equal to the algebraic sum of the moments of the couples.
Let $(P, p), (Q, q), (R, r), …$ be the number of couples acting in the same plane upon a body.

Since the couples of equal moments in the sme plane are equivalent, the couple $(Q, q)$ can be replaced by the couple $(X, p)$, such that \[X×p=Q×q\] \[X=\frac{Qq}{p}\]
Hence, by the couple
\[\left(\frac{Qq}{p}, \text{ }p\right)\]
Similarly, the couple $(R, r)$ can be replaced by
\[\left(\frac{Rr}{p}, \text{ } p\right)\]
If we replace all the couples in this way, then a single couple is obtained with the arm $p$ having component forces equal to
\[\left(P+\frac{Qq}{p}+\frac{Rr}{p}+…\right)\]
Hence, the moment of the single couple is equal to
\[\left(P+\frac{Qq}{p}+\frac{Rr}{p}+…\right)×p\]
\[=Pp+Qq+Rr+…\] which is the algebraic sum of the moments of the given couples.
Theorem 5: A force and a couple acting in the same plane upon a rigid body are equivalent to a single force, equal and parallel to the original single force.
Let $F$ be the given force acting at $O$ along $OA$ and let the couple be $(P, p)$.

Replace the given couple by another couple having its forces each equal to $F$. Let the arm of the new couple be $x$. Then, its moment is equal to the moment of the original couple, i.e.
\[F×x=P×p\] \[x=\frac{Pp}{F}\]
Now, place the couple such that one of its component force $F$ acts at $O$ along the line of the action of the given force $F$ but in opposite direction i.e. it acts along $OB$.

The two equal forces acting along $OA$ and $OB$ balance each other and a single force $F$ is left at $C$ which is parallel to the original force. Thus, a force $F$ and a couple $(P, p)$ are equivalent to a single force $F$ equal and parallel to the original force but displaced to a distance \[\frac{Pp}{F}\] from its original position.
Theorem 6: If three forces, acting upon a rigid body, be represented in magnitude, direction and line of action by the sides of a triangle taken in order, they are equivalent to a couple whose moment is represented by twice the area of the triangle.
Let $ABC$ be the triangle whose sides $BC$, $CA$ and $AB$ represent the three forces $P$, $Q$ and $R$ respectively, acting upon a rigid body.

Draw $DAE$ parallel to $BC$. Let two equal and opposite forces $P$ act along $AD$ and $AE$. Draw $AN⊥BC$. By triangle law of forces, the three forces $P$ along $AD$, $Q$ along $AC$ and $R$ along $AB$ are in equilibrium.
Hence, two forces are left; $P$ along $AE$ and $P$ along $BC$. These two forces form a couple of moment
\[=P × AN\]
\[=BC×AN\]
\[=2×\left(\frac{1}{2}BC×AN\right)\]
\[=2×∆ABC\]
Hence, three forces represented by the sides of a traingle taken in order are equivalent to a couple whose moment is equal to the twice the area of the triangle.
