To find the maxima and minima (maximum and minimum) value of a function $ƒ$ in an interval $(a,b)$, it is necessary to know the nature of the curve in the neighborhood of the point where the maximum or minimum value of the function occurs. The nature of the curve at a particular point is known by studying the slopes of the tangents at the point in its neighborhood. The slope or the gradient of a tangent line at a point of the graph of a function $ƒ$ may be positive, negative or zero.
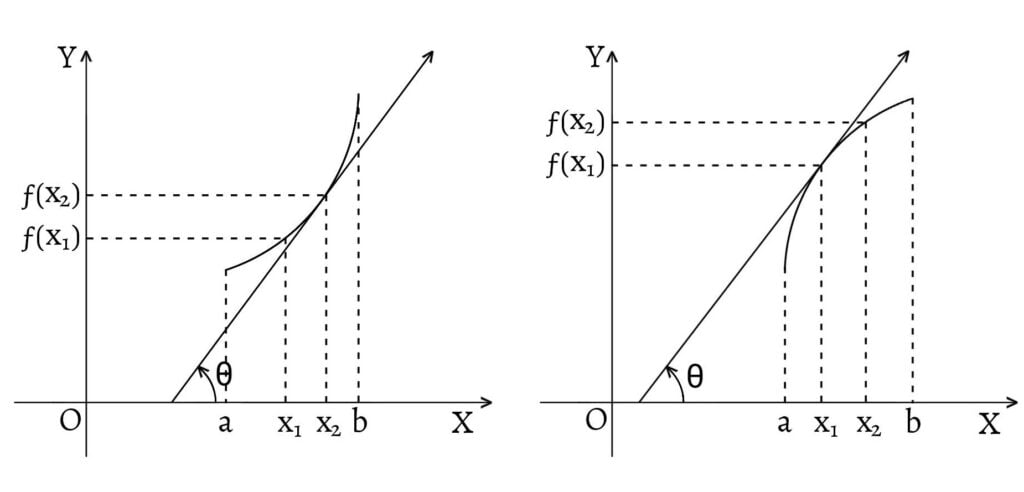
If the slope of $ƒ(x)$ is positive $\left(\text{i.e. } ƒ'(x)>0\right)$, the inclination $\theta$ of the tangent line is positive and the tangent line slopes upwards from left to right as shown in above figure. In the figures, within the interval $(a,b)$, where the slope of the tangent line at any point is positive, \[x_2>x_1\Rightarrow ƒ(x_2)>ƒ(x_1)\] i.e. the function is increasing in its neighborhood.

If the slope of $ƒ(x)$ is negative $\left(\text{i.e. } ƒ'(x)<0\right)$, the inclination $\theta$ of the tangent line is negative and the tangent line slopes downwards from left to right as shown in above figure. In the figures, within the interval $(a,b)$, where the slope of the tangent line at any point is negative, \[x_2>x_1\Rightarrow ƒ(x_2)<ƒ(x_1)\] i.e. the function is decreasing in its neighborhood.
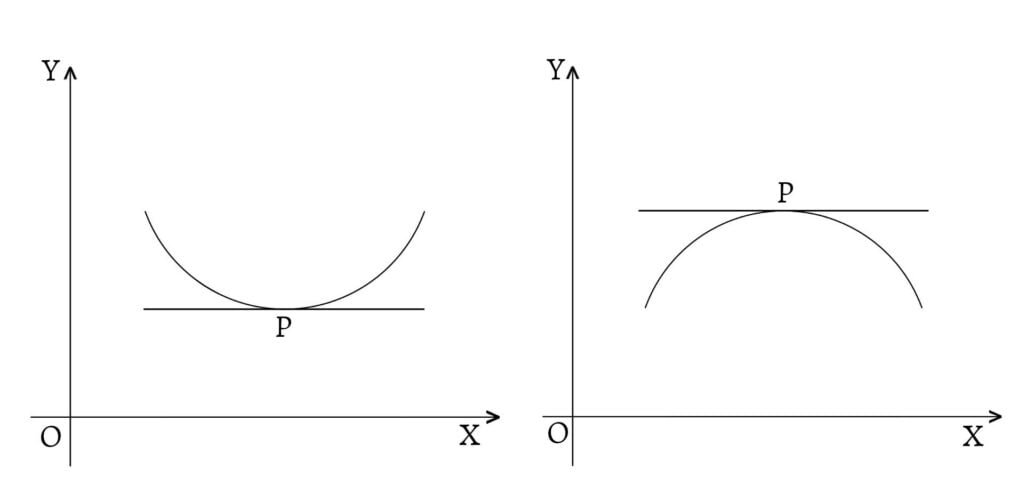
If the slope of $ƒ(x)$ is zero $\left(\text{i.e. }ƒ'(x)=0\right)$, the tangent line neither slopes upwards nor downwards i.e. it remains horizontal or stationary. The points at which $ƒ'(x)=0$ or $ƒ'(x)$ is not defined are called critical (or stationary) points.

$ƒ^{\prime\prime}(x)$ is the derivative of $ƒ'(x)$. If $ƒ^{\prime\prime}(x)>0$, $ƒ'(x)$ is increasing i.e. the slope of the tangent line is increasing. In the figure $\text{(a)}$, the slope $ƒ'(x)$ is increasing from a smaller positive value to a larger positive value and in the figure $\text{(b)}$, the slope is increasing from a larger negative value to a smaller negative value. The curve in the figure $\text{(c)}$ is just a combination of the figures $\text{(a)}$ and $\text{(b)}$. These curves are said to be concave upwards. Hence, if $ƒ^{\prime\prime}(x)>0$ in an interval $(a,b)$, the graph of $ƒ$ is concave upwards in the interval.

If $ƒ^{\prime\prime}(x)<0$, $ƒ'(x)$ is decreasing i.e. the slope of the tangent line is decreasing. In the figure $\text{(a’)}$, the slope $ƒ'(x)$ is decreasing from a larger positive value to a smaller positive value, while in the figure $\text{(b’)}$, the slope is decreasing from a smaller negative value to a larger negative value. The curve in the figure $\text{(c’)}$ is just a combination of the figures $\text{(a’)}$ and $\text{(b’)}$. These curves are said to be concave downwards. Hence, if $ƒ^{\prime\prime}(x)<0$ in an interval $(a,b)$, the graph of $ƒ$ is concave downwards in the interval.

Consider a function $ƒ$ with a portion of curve concave downwards in the interval $(a,b)$ as shown in figure. Hence, $ƒ^{\prime\prime}(x)<0$ so $ƒ'(x)$ decreases throughout the portion of the curve in the interval $(a,b)$. But in the interval $(a,c)$, $ƒ'(x)>0$ and in the interval $(c,b)$, $ƒ'(x)<0$. As the curve is continuous, there must exist a point $x_o$ such that $ƒ'(x_o)=0$ and at that point $x_o$, the function $ƒ$ has a local maximum. So, the conditions for a function $ƒ$ to have a local maximum at a point $x_o$ are \[\text{1. } ƒ'(x_o)=0\] \[\text{2. } ƒ^{\prime\prime}(x_o)<0\]
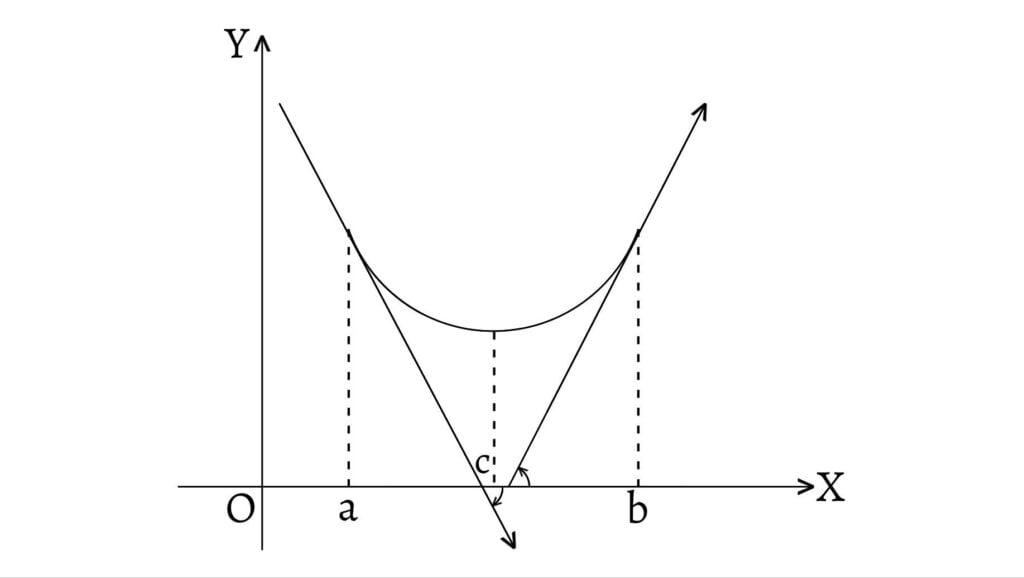
Similarly, consider a function $ƒ$ with a portion of curve concave upwards in the interval $(a,b)$ as shown in figure. Hence, $ƒ^{\prime\prime}(x)>0$ so $ƒ'(x)$ increases throughout the portion of the curve in the interval $(a,b)$. But in the interval $(a,c)$, $ƒ'(x)<0$ and in the interval $(c,b)$, $ƒ'(x)>0$. As the curve is continuous, there must exist a point $x_o$ such that $ƒ'(x_o)=0$ and at that point $x_o$, the function $ƒ$ has a local minimum. So, the conditions for a function $ƒ$ to have a local minimum at a point $x_o$ are \[\text{1. } ƒ'(x_o)=0\] \[\text{2. } ƒ^{\prime\prime}(x_o)>0\]

Again, consider the graph of a function $ƒ$ as shown in the figure. The portion of the graph in the interval $(a,c)$ is concave downwards so $ƒ^{\prime\prime}(x)<0$, while the portion of the graph in the interval $(c,b)$ is concave upwards so $ƒ^{\prime\prime}(x)>0$. Hence, there must exist a point in the interval at which $ƒ^{\prime\prime}(x)=0$. This point of the graph is called a point of inflection and it separates the portion of the graph which is concave downwards from the portion which is concave upwards.
The local maxima and local minima are not necessarily the greatest and the least values of the function but simply the maximum and minimum values on the neighborhood of the point $x=a$. A function may have several maximum and minimum values which occur alternatively. But besides these maximum and minimum values, there may be the values greater than the maximum value and less than the minimum value i.e. there may be the greatest and the least values of the function which are termed as absolute maximum value and the absolute minimum value of the function.
Hence, we have the following definitions for the following terms:
Absolute Maxima
A function $y=ƒ(x)$ is said to have the absolute maximum value or absolute maxima at $x=a$ if $ƒ(a)$ is the greatest of all of its values for all $x$ belonging to the domain of the function. The absolute maximum value is also known as the global maximum value.
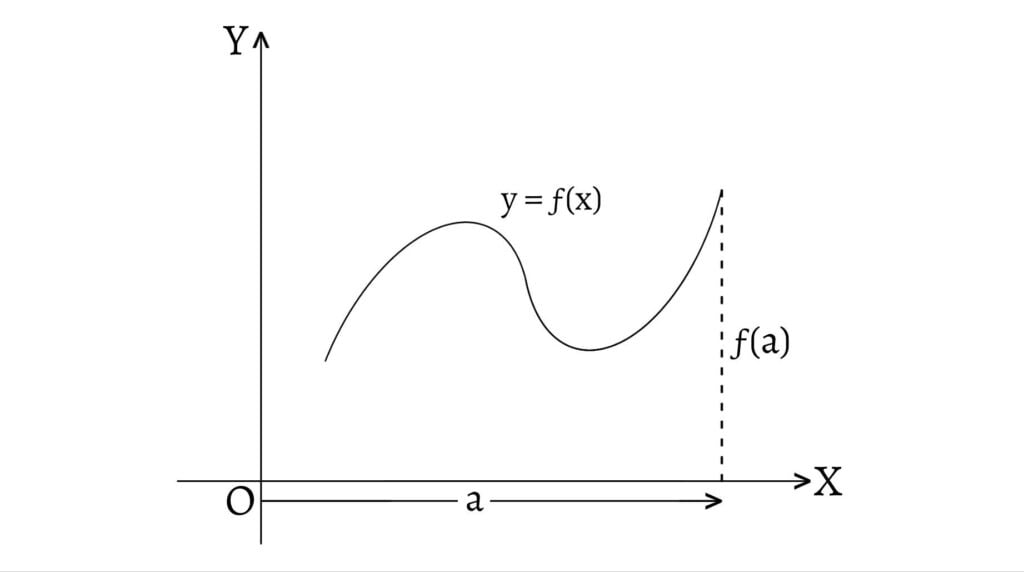
In other words, $ƒ(a)$ is the absolute maximum value of $ƒ(x)$ if $ƒ(a)≥ƒ(x)$ for all $x\in D(ƒ)$. In the figure, $ƒ(a)$ is the absolute maximum value of $ƒ(x)$ at $x=a$.
Absolute Minima
A function $y=ƒ(x)$ is said to have the absolute minimum value or absolute minima at $x=a$ if $ƒ(a)$ is the smallest of all of its values for all $x$ belonging to the domain of the function. The absolute minimum value is also known as the global minimum value.

In other words, $ƒ(a)$ is the absolute minimum value of $ƒ(x)$ if $ƒ(a)≤ƒ(x)$ for all $x\in D(ƒ)$. In the figure, $ƒ(a)$ is the absolute minimum value of $ƒ(x)$ at $x=a$.
Stationary Point
A point on the graph of the function $y=ƒ(x)$ where the tangent is parallel to the $\text{X-axis}$ is known as the stationary point or critical point. At the stationary point, \[\frac{dy}{dx}=ƒ'(x)=0\]
Local Maxima
A function $y=ƒ(x)$ is said to have the local maximum value or local maxima at $x=a$ if $ƒ(a)>ƒ(a\pm h)$ for sufficiently small positive value of $h$. The local maxima is also known as the relative maxima of the function.
Local Minima
A function $y=ƒ(x)$ is said to have the local minimum value or local minima at $x=a$ if $ƒ(a)<ƒ(a\pm h)$ for sufficiently small positive value of $h$. The local minima is also known as the relative minima of the function.
Concavity and Convexity of Curves
The graph of the function $y=ƒ(x)$ defined in an interval $(a,b)$ is concave upward (or convex downward) if each point (except the point of contact) on the graph (i.e. curve) lies above any tangent to it in that interval.
But if each point on the graph (i.e. curve) lies below any tangent to the curve in the interval, then the graph of the function is said to be concave downward (or convex upward).
The graph of the function $y=ƒ(x)$ will be concave upward if $\frac{d^2y}{dx^2}=ƒ^{\prime\prime}(x)>0$ and it will be concave downward if $\frac{d^2y}{dx^2}=ƒ^{\prime\prime}(x)<0$.
Point of Inflection
The point which divides the graph of the function from the shape of upward concavity (or downward concavity) to the downward concavity (or upward concavity) is known as the point of inflection. If $y=ƒ(x)$ represents a continuous curve, then the point where $\frac{d^2y}{dx^2}=ƒ^{\prime\prime}(x)=0$ and $\frac{d^3y}{dx^3}=ƒ^{\prime\prime\prime}(x)≠0$ is said to be the point of inflection.
Find the absolute maximum and the absolute minimum values of the function $ƒ(x)=2x^3-15x^2+36x+10$ on $[1,4]$.
Here, \[ƒ(x)=2x^3-15x^2+36x+10\] \[\therefore ƒ'(x)=6x^2-30x+36\] For stationary point, \[ƒ'(x)=0\] \[6x^2-30x+36=0\] \[x^2-5x+6=0\] \[(x-2)(x-3)=0\] \[\text{either, }x=2 \text{ or, } x=3\] \[\therefore ƒ(2)=2×2^3-15×2^2+36×2+10=38\] \[ƒ(3)=2×3^3-15×3^2+36×3+10=37\] \[ƒ(1)=2×1^3-15×1^2+36×1+10=33\] \[ƒ(4)=2×4^3-15×4^2+36×4+10=42\] \[\therefore \text{Absolute Maximum}=42 \text{ at }x=4\] \[\text{Absolute Minimum}=33\text{ at }x=1\]
Find the local maxima, the local minima and the point of inflection of the function $ƒ=x^3-6x^2+3$.
Here, \[ƒ(x)=x^3-6x^2+3\] \[\therefore ƒ'(x)=3x^2-12x\] \[ƒ^{\prime\prime}(x)=6x-12\] For stationary point, \[ƒ'(x)=0\] \[3x^2-12x=0\] \[x(x-4)=0\] \[\therefore x=0,4\] Now, \[ƒ^{\prime\prime}(0)=0-12=-12<0\] \[\therefore ƒ(x) \text{ is max. at } x=0.\] \[\therefore \text{max. value }(ƒ_{\text{max}})=0-0+3=3\] And, \[ƒ^{\prime\prime}(4)=6×4-12=12>0\] \[\therefore ƒ(x) \text{ is mini. at } x=4.\] \[\therefore \text{mini. value } (ƒ_{\text{mini}})=4^3-6×4^2+3\]\[=-29\] For point of inflection, \[ƒ^{\prime\prime}(x)=0\] \[6x-12=0\] \[\therefore x=2\] Thus, the point of inflection is at $x=2$.
Find the local maxima, the local minima and the point of inflection of the function $ƒ(x)=3x^2-6x+3$.
Here, \[ƒ(x)=3x^2-6x+3\] \[ƒ'(x)=6x-6\] \[ƒ^{\prime\prime}(x)=6\] For stationary point, \[ƒ'(x)=0\] \[6x-6=0\] \[\therefore x=1\] Now, \[ƒ^{\prime\prime}(1)=6>0\] \[\therefore ƒ(x) \text{ is mini at } x=1.\] \[\text{mini. value }(ƒ_{\text{mini}})=3×1-6×1+3=0\] For point of inflection, \[ƒ^{\prime\prime}(x)=0\] \[6=0 \text{ [No solution]}\] Hence, point of inflection does not exist.
Show that the function $ƒ(x)=x^3-6x^2+12x-3$ has neither maximum nor minimum value.
Here, \[ƒ(x)=x^3-6x^2+12x-3\] \[\therefore ƒ'(x)=3x^2-12x+12\] \[ƒ^{\prime\prime}(x)=6x-12\] For stationary point, \[ƒ'(x)=0\] \[3x^2-12x+12=0\] \[x^2-4x+4=0\] \[(x-2)^2=0\] \[x=2\] Now, \[ƒ^{\prime\prime}(2)=6×2-12=0\] Hence, $ƒ(x)$ has neither maximum nor minimum value.
Determine where the graph is concave upwards and where it is concave downwards of the function $ƒ(x)=x^4-8x^3+18x^2-24$.
Here, \[ƒ(x)=x^4-8x^3+18x^2-24$\] \[\therefore ƒ'(x)=4x^3-24x^2+36x\] \[ƒ^{\prime\prime}(x)=12x^2-48x+36\] Now, curve will be concave downwards if \[ƒ^{\prime\prime}(x)<0\] \[12x^2-48x+36<0\] \[x^2-4x+3<0\] \[(x-1)(x-3)<0\] \[\text{either, } (x-1)>0 \text{ and } (x-3)<0\] \[x>1 \text{ and } x<3\] \[\text{or, } (x-1)<0 \text{ and } (x-3)>0\] \[x<1 \text{ and } x>3\]

Hence, curve is concave downwards on $(1,3)$ and concave upwards on $(-\infty,1)\cup(3,\infty)$.
A window is in the form of a rectangle surmounted by a semi-circle. If the total perimeter is $9$ metres, find the radius of the semi-circle for the greatest window area

Let $ABCD$ be the rectangular part of the window. \[AB=x=CD=\text{diameter}\] \[BC=y=DA\] Then, \[\text{Radius }(r)=\frac{x}{2}\] Now, \[AB+BC+\overset{\huge\frown}{CD}+DA=9\] \[x+y+\frac{1}{2}(2πr)+y=9\] \[x+y+\frac{πx}{2}+y=9\] \[2y+\left(1+\frac{π}{2}\right)x=9\] \[2y=9-\left(\frac{π+2}{2}\right)x\] \[y=\frac{9}{2}-\left(\frac{π+2}{4}\right)x\] And, \[\text{Area }(A)=xy+\frac{1}{2}πr^2\] \[A=x\left[\frac{9}{2}-\frac{(π+2)x}{4}\right]+\frac{1}{2}π\frac{x^2}{4}\] \[A=\frac{9x}{2}-\frac{(π+2)x^2}{4}+\frac{π}{8}x^2\] \[A=\frac{9x}{2}-\left(\frac{π+4}{8}\right)x^2\] \[\therefore A(x)=\frac{9x}{2}-\left(\frac{π+4}{8}\right)x^2\] \[A'(x)=\frac{9}{2}-\left(\frac{π+4}{4}\right)x\] \[A^{\prime\prime}(x)=-\left(\frac{π+4}{4}\right)\] For stationary point, \[A'(x)=0\] \[\frac{9}{2}-\left(\frac{π+4}{4}\right)x=0\] \[\frac{9}{2}=\left(\frac{π+4}{4}\right)x\] \[18=(π+4)x\] \[\therefore x=\frac{18}{π+4}\] Now, \[A^{\prime\prime}\left(\frac{18}{π+4}\right)=-\left(\frac{π+4}{4}\right)<0\] Therefore, $A(x)$ is max. at $x=\frac{18}{π+4}$. \[\therefore r=\frac{1}{2}\left(\frac{18}{π+4}\right)=\frac{9}{π+4}\]
Find two numbers whose sum is 10 and the sum of whose squares is minimum.
Let those two numbers be $x$ and $y$. Then, \[x+y=10\] \[y=10-x\] And, \[S=x^2+y^2\] \[S=x^2+(10-x)^2\] \[S=x^2+100-20x+x^2\] \[\therefore S(x)=2x^2-20x+100\] \[S'(x)=4x-20\] \[S^{\prime\prime}(x)=4\] For stationary point, \[S'(x)=0\] \[4x-20=0\] \[x=5\] Now, \[S^{\prime\prime}(x)=4>0\] Therefore, $S(x)$ is mini at $x=5$. And, \[y=10-5=5\] Hence, the required two numbers are 5 and 5.
