Parallelogram law of vector addition states that if two vectors starting from a point represent two adjacent sides of a parallelogram then the diagonal starting from same point represents the resultant magnitude and direction of those two vectors.
Consider two vectors. \[\overrightarrow{a}=\overrightarrow{OA}=(a_1,a_2)\] \[\overrightarrow{b}=\overrightarrow{OB}=(b_1,b_2)\]
Then the sum of the vectors $\overrightarrow{a}$ and $\overrightarrow{b}$ is defined by \[\overrightarrow{a}+\overrightarrow{b}=(a_1,a_2)+(b_1,b_2)\] \[\therefore\overrightarrow{a}+\overrightarrow{b}=(a_1+b_1,a_2+b_2)\text{ __(1)}\]
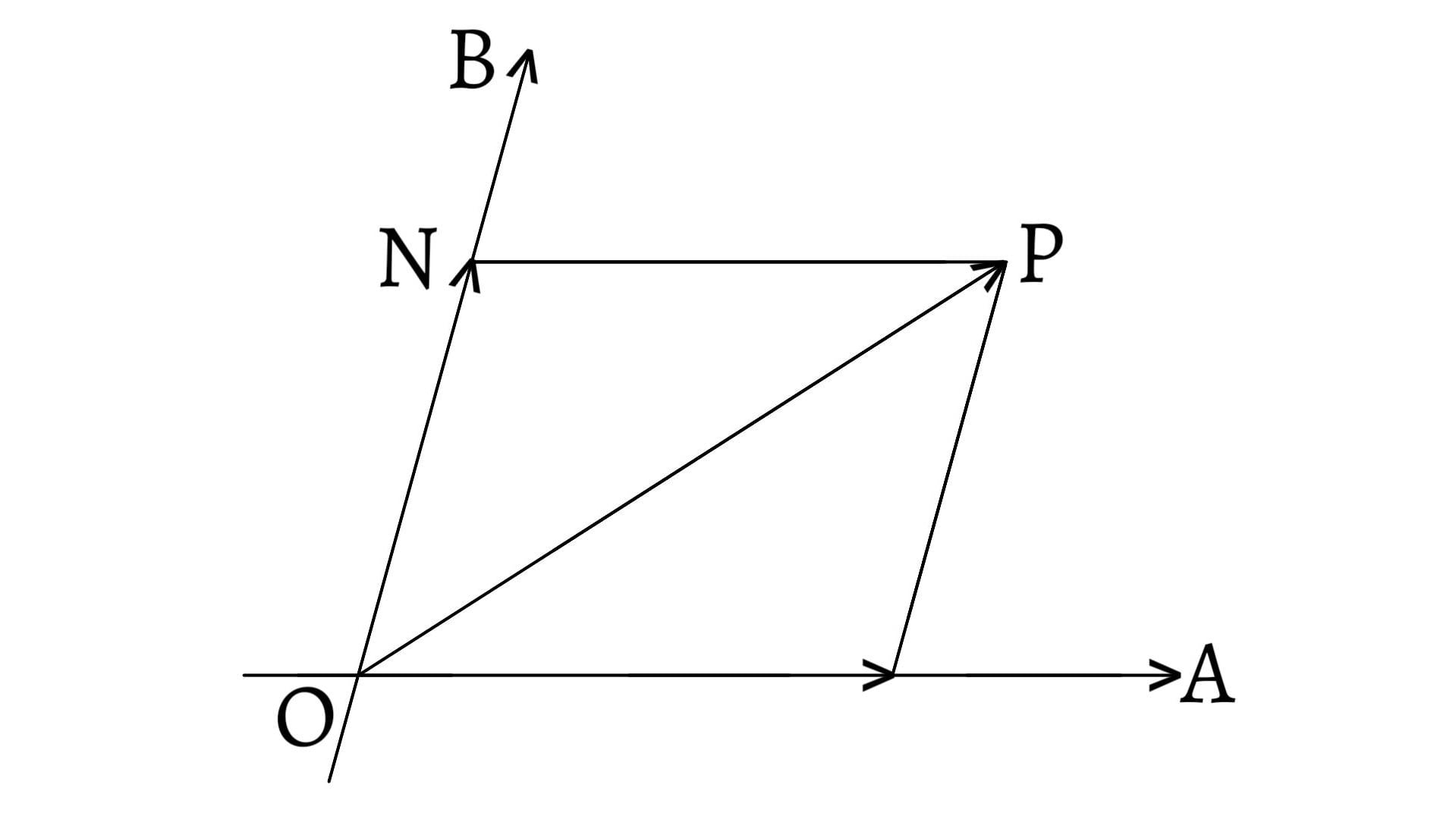
Now, draw a parallelogram $OACB$ with magnitudes of $\overrightarrow{OA}$ and $\overrightarrow{OB}$ as its adjacent sides. Join $OC$. From $A$, $B$ and $C$, draw $AP$, $BQ$ and $CR$ perpendiculars to $OX$. Again, from $A$ and $C$, draw $AN$ and $CM$ perpendiculars to $CR$ and $OY$ respectively.
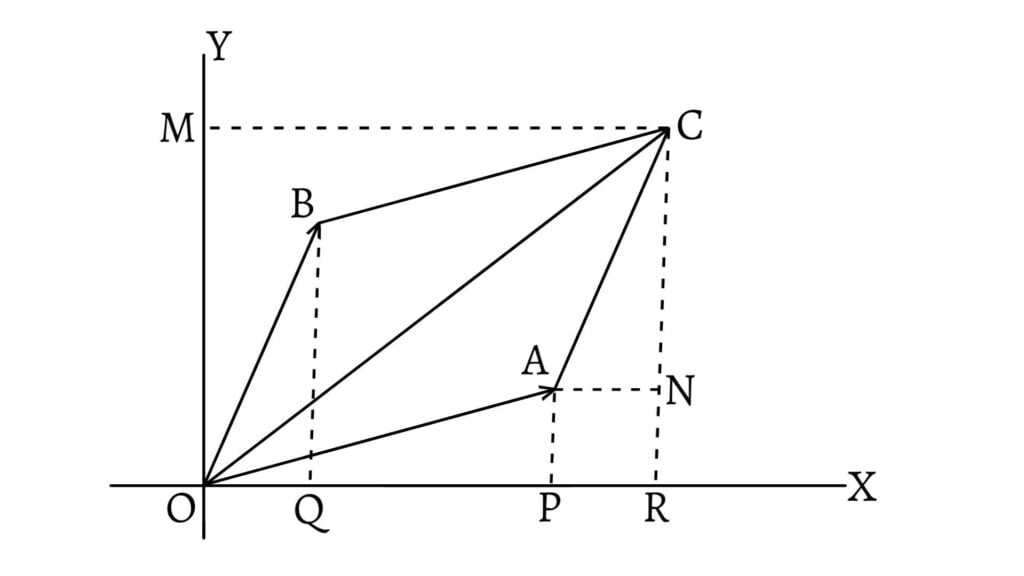
\[\begin{array}{c}\text{Then,}\;&OP=a_1,&PA=a_2\\ \text{and,}\;&OQ=b_1&QB=b_2\end{array}\]
Since, $OB$ and $OQ$ are parallel to $AC$ and $AN$ respectively and also $OB=AC$, so the two triangles $OQB$ and $ANC$ are congruent. \[\therefore OQ=AN\] \[\therefore PR=AN=OQ=b_1\] \[\text{also,}\;CN=QB=b_2\]
Now, projection of $OC$ on x-axis \[=OR=OP+PR=a_1+b_1\]
Again, projection of $OC$ on y-axis \[=OM=RC=RN+NC\] \[=PA+QB=a_2+b_2\] \[\therefore\overrightarrow{OC}=(OR,RM)=(OR,RC)\] \[\therefore\overrightarrow{OC}=(a_1+b_1,a_2+b_2)\text{ __(2)}\]
Also, we have, \[\overrightarrow{OA}+\overrightarrow{OB}=(a_1,a_2)+(b_1,b_2)\text{ __(3)}\] Hence, from $\text{(1)}$, $\text{(2)}$ and $\text{(3)}$, \[\overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{OC}\]
Thus, the sum of the vectors $\overrightarrow{OA}$ and $\overrightarrow{OB}$ is represented by $\overrightarrow{OC}$, the vector represented by the diagonal of the parallelogram having the magnitudes of $\overrightarrow{OA}$ and $\overrightarrow{OB}$ as its adjacent sides. This is the parallelogram law of vector addition.
It states that if a particle simultaneously possesses two vectors represented in magnitude and direction by the two adjacent sides of a parallelogram drawn from a point, then the resultant vector is represented both in magnitude and direction by the diagonal passing through the same point.
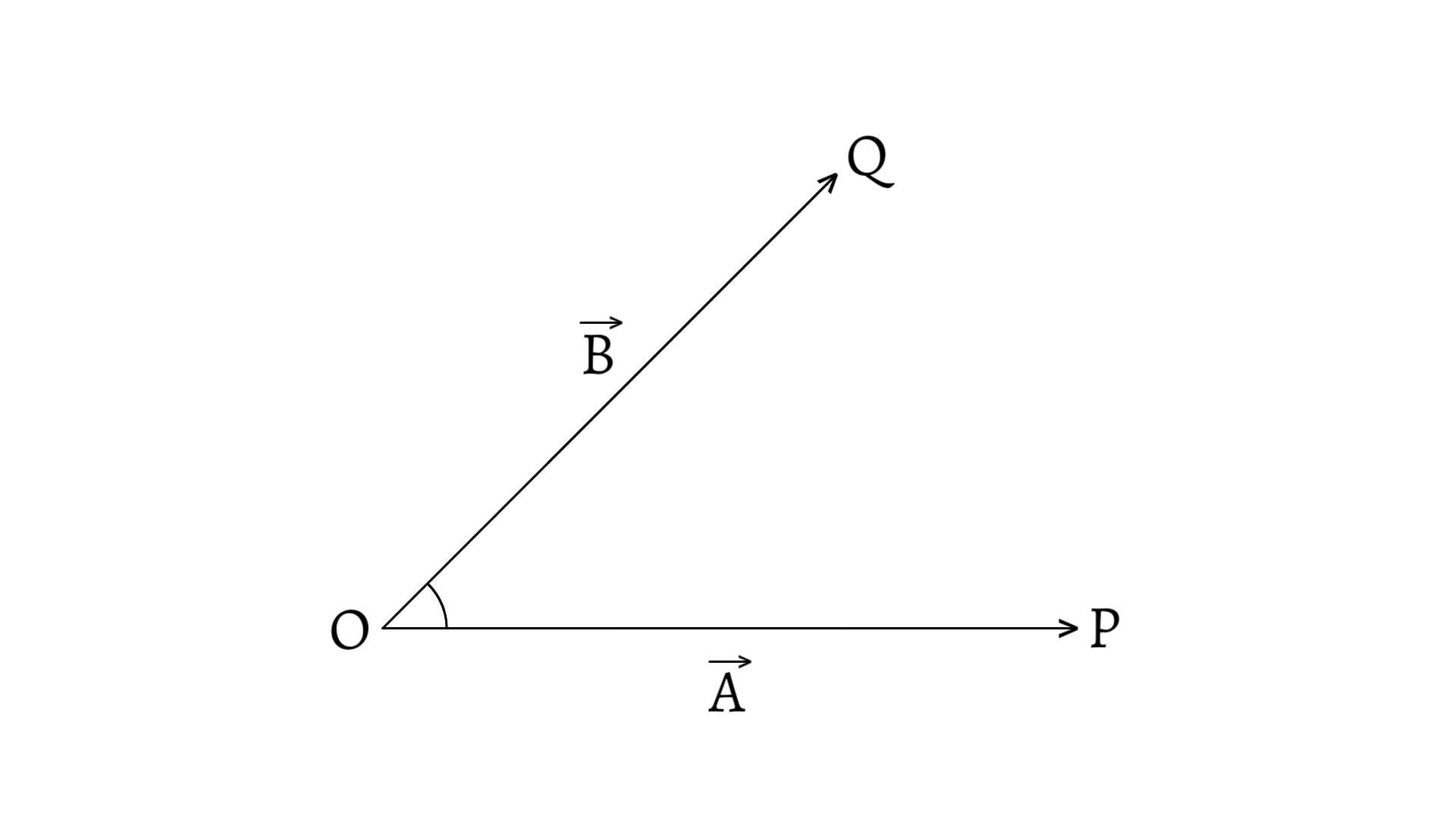
Consider two vectors $\overrightarrow{P}$ and $\overrightarrow{Q}$ represented in magnitude and direction by the two adjacent sides $\overrightarrow{AB}$ and $\overrightarrow{AD}$ of a parallelogram $ABCD$. Let $\theta$ be the angle between them. Then, the diagonal $\overrightarrow{AC}$ of the parallelogram represents the resultant $\overrightarrow{R}$ of the vectors $\overrightarrow{P}$ and $\overrightarrow{Q}$ in magnitude and direction.
Magnitude of $\overrightarrow{R}$
From $C$, draw $CM\perp AB$, produced upto $M$.

By using Pythagoras theorem in right angled $\Delta AMC$, \[AC^2 = AM^2 + MC^2\] \[AC^2 = (AB + BM)^2+ MC^2 \text{ __(a)}\] \[\text{and,}\; \sin\theta=\frac{MC}{BC}\] \[\therefore MC=Q\sin\theta \text{ __(b)}\] \[\text{Similarly,}\;\cos\theta=\frac{BM}{BC}\] \[\therefore BM=Q\cos\theta \text{ __(c)}\] \[\text{From (a),}\;R^2 = (P + Q\cos\theta)^2+ (Q\sin\theta)^2\] \[R^2 = P^2+ 2PQ\cos\theta + Q^2\cos^2\theta + Q^2\sin^2\theta\] \[R^2= P^2+ 2PQ\cos\theta + Q^2 (\cos^2\theta + \sin^2\theta)\] \[R^2= P^2+ 2PQ\cos\theta + Q^2\] \[\therefore R^2 = \sqrt{P^2 + 2PQ\cos\theta + Q^2}\]
Let the angle of the resultant $\overrightarrow{R}$ with the vector $\overrightarrow{P}$ be $\beta$. \[\text{Then,}\;\tan\beta = \frac{MC}{AM}\] \[\tan\beta = \frac{Q\sin\theta}{P+Q\cos\theta}\] \[\therefore\beta=\tan^{-1}\left(\frac{Q\sin\theta}{P+Q\cos\theta}\right)\]
Special Cases
Case I:
When the vectors are parallel to each other, i.e. $\theta=0°$, \[R^2 = \sqrt{P^2 + 2PQcos0 + Q^2}\] \[R^2 = \sqrt{P^2 + 2PQ + Q^2}\] \[R^2 = \sqrt{(P + Q)^2}\] \[∴R = P + Q\;\text{(Maximum value of R)}\]
Case II:
When the vectors are perpendicular to each other, i.e. $\theta=90°$, \[R^2 = \sqrt{P^2+ 2PQcos90 + Q^2}\] \[\therefore R^2 = \sqrt{P^2 + Q^2}\]
Case III:
When the angle between the vectors $(\theta)$ is $180°$. \[\text{Then,}\; R^2 = \sqrt{P² + 2PQcos180 + Q²}\] \[R^2 = \sqrt{P^2 – 2PQ + Q^2}\] \[R^2 = \sqrt{(P – Q)^2}\] \[\therefore R = P – Q\;\text{(Minimum Value of R)}\]
Previous: Composition of Vectors