Application of Dot Product

As an application of dot product of two vectors, we use it to prove the following formulae.

---

cos(A-B)=cosAcosB+sinAsinB

Let $O$ be the origin and, $OX$ and $OY$ be the two mutually perpendicular straight lines representing x-axis and y-axis respectively.

Let $\angle XOS=B$ and $\angle XOR=A$ so that $\angle XOR=A-B$.

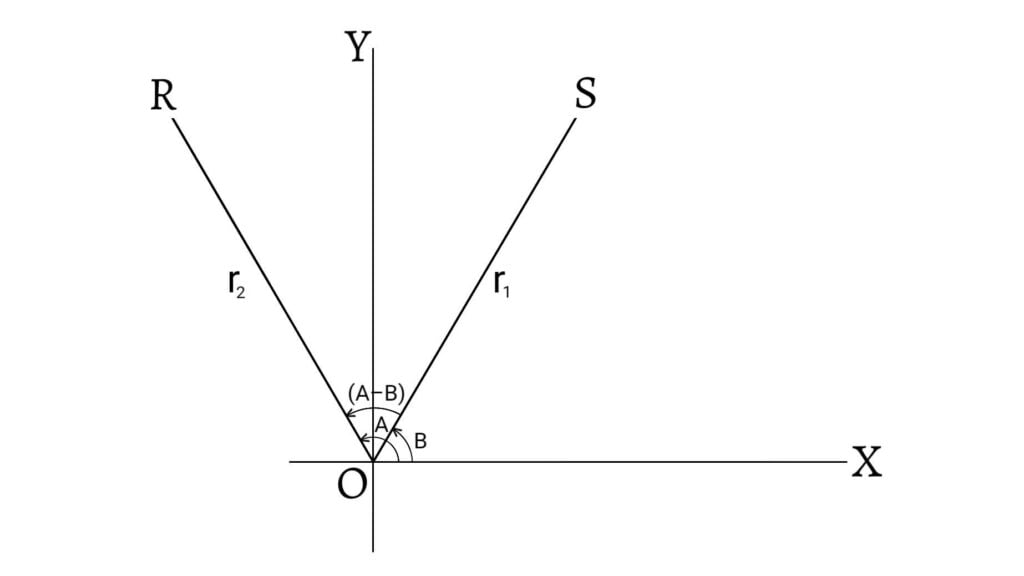
Again, let $OS=r_1$ and $OR=r_2$. Then, the coordinates of $S$ and $R$ are $(r_1\cos B, r_1\sin B)$ and $(r_2\cos A, r_2\sin A)$ respectively.

\[\therefore\overrightarrow{OS}=(r_1\cos B, r_1\sin B)\] \[\text{and,}\;\overrightarrow{OR}=(r_2\cos A, r_2\sin A)\] Then, \[\overrightarrow{OS}\cdot\overrightarrow{OR}=(r_1\cos B, r_1\sin B)\cdot(r_2\cos A, r_2\sin A)\] \[=r_1r_2\cos A\cos B+r_1r_2\sin A\sin B\] \[=r_1r_2(\cos A\cos B+\sin A\sin B)\]

Since $(A-B)$ is the angle between $OS$ and $OR$, so \[\cos(A-B)=\frac{\overrightarrow{OS}\cdot \overrightarrow{OR}}{|\overrightarrow{OS}||\overrightarrow{OR}|}\] \[=\frac{r_1r_2(\cos A\cos B+\sin A\sin B)}{r_1r_2}\] \[=\cos A\cos B+\sin A\sin B\] \[\therefore\cos(A-B)=\cos A\cos B+\sin A\sin B\]

---

cos(A+B)=cosAcosB-sinAsinB

Let $O$ be the origin and, $OX$ and $OY$ be the two mutually perpendicular straight lines representing x-axis and y-axis respectively.

Let $\angle XOS=A$ and $\angle XOR=B$ so that $\angle XOR=A+B$.

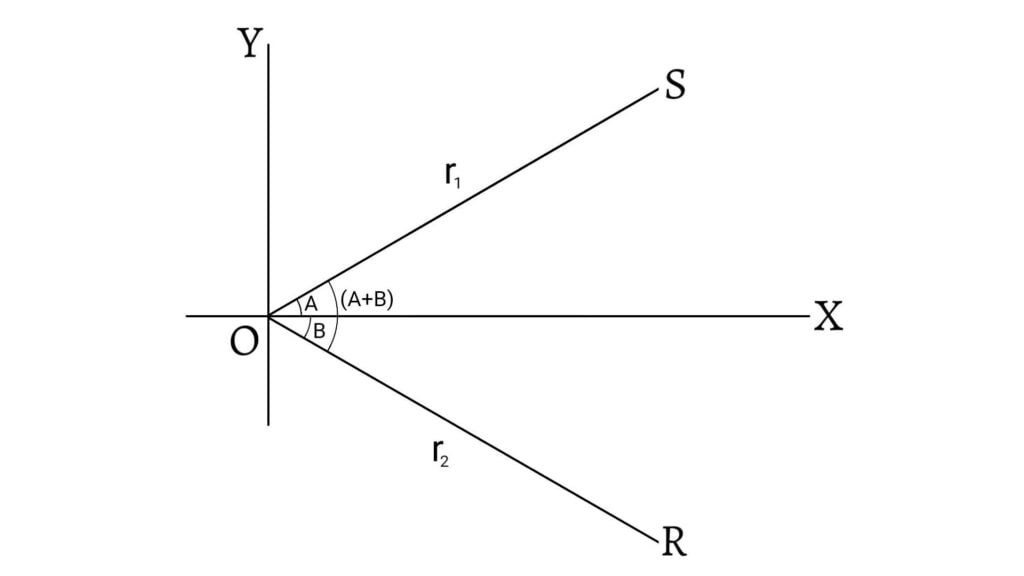
Again, let $OS=r_1$ and $OR=r_2$. Then, the coordinates of $S$ and $R$ are $(r_1\cos A, r_1\sin A)$ and $(r_2\cos B, -r_2\sin B)$ respectively.

\[\therefore\overrightarrow{OS}=(r_1\cos A, r_1\sin A)\] \[\text{and,}\;\overrightarrow{OR}=(r_2\cos B, -r_2\sin B)\] Then, \[\overrightarrow{OS}\cdot\overrightarrow{OR}=(r_1\cos A, r_1\sin A)\cdot(r_2\cos B, -r_2\sin B)\] \[=r_1r_2\cos A\cos B-r_1r_2\sin A\sin B\] \[=r_1r_2(\cos A\cos B-\sin A\sin B)\]

Since $(A+B)$ is the angle between $OS$ and $OR$, so \[\cos(A-B)=\frac{\overrightarrow{OS}\cdot \overrightarrow{OR}}{|\overrightarrow{OS}||\overrightarrow{OR}|}\] \[=\frac{r_1r_2(\cos A\cos B-\sin A\sin B)}{r_1r_2}\] \[=\cos A\cos B-\sin A\sin B\] \[\therefore\cos(A+B)=\cos A\cos B-\sin A\sin B\]

---

$a^2=b^2+c^2-2bc\cos A$

In $\Delta ABC$, let $\overrightarrow{BC}=\overrightarrow{a}$, $\overrightarrow{CA}=\overrightarrow{b}$ and $\overrightarrow{AB}=\overrightarrow{c}$.

By triangle law of vector addition, \[\overrightarrow{BC}=\overrightarrow{BA}+\overrightarrow{AC}\] \[\overrightarrow{a}=-\overrightarrow{c}-\overrightarrow{b}\] Squaring both sides, \[a^2=c^2+b^2+2\: \overrightarrow{b}\:\overrightarrow{c}\] \[a^2=b^2+c^2+2bc\cos(π-A)\] \[\therefore a^2=b^2+c^2-2bc\cos A\]

Similarly, we can prove: \[b^2=c^2+a^2-2ca\cos B\] \[c^2=a^2+b^2-2ab\cos C\]

---

$a=c\cos B+b\cos C$

In $\Delta ABC$, let $\overrightarrow{BC}=\overrightarrow{a}$, $\overrightarrow{CA}=\overrightarrow{b}$ and $\overrightarrow{AB}=\overrightarrow{c}$.

By triangle law of vector addition, \[\overrightarrow{BC}=\overrightarrow{BA}+\overrightarrow{AC}\] \[\overrightarrow{a}=-\overrightarrow{c}-\overrightarrow{b}\] Multiplying each term scalarly by $\overrightarrow{a}$, we get,

\[\overrightarrow{a}\cdot\overrightarrow{a}=-\overrightarrow{a}\cdot\overrightarrow{c}-\overrightarrow{a}\cdot\overrightarrow{b}\] \[a^2=-ac\cos(π-B)-ab\cos(π-C)\] \[a^2=ac\cos B+ab\cos C\] \[\therefore a=c\cos B+b\cos C\]

Similarly, we can prove: \[b=c\cos A+a\cos C\] \[c=a\cos B+b\cos A\]

---

---