As an application of cross product of two vectors, we use it to prove the following formulae.
sin(A+B)=sinAcosB+cosAsinB
Let $XOX’$ and $YOY’$ be two mutually perpendicular straight lines representing x-axis and y-axis respectively. Let $\angle XOM=A$ and $\angle X’ON=B$ so that $\angle MON=π-(A+B)$.
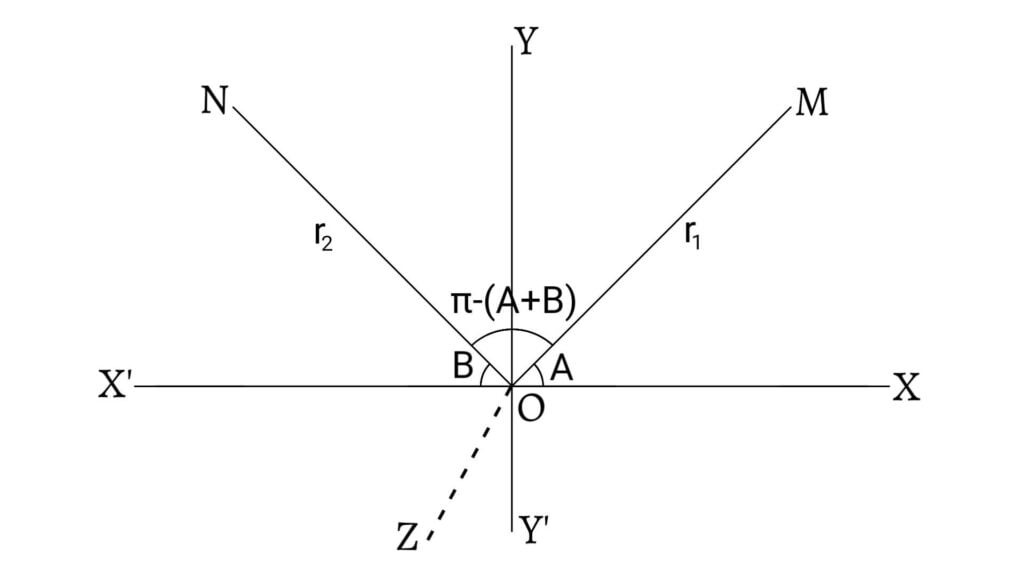
Let $OM=r_1$ and $ON=r_2$. Then, the coordinates of $M$ and $N$ are $(r_1\cos A, r_1\sin A)$ and $(r_2\cos(π-B), r_2\sin(π-B))$ respectively.
\[\therefore\overrightarrow{OM}=(r_1\cos A, r_1\sin A, 0)\] and, \[\overrightarrow{ON}=(r_2\cos(π-B), r_2\sin(π-B), 0)\] \[=(-r_2\cos B, r_2\sin B, 0)\]
Now, \[\begin{array}{c}\overrightarrow{OM}×\overrightarrow{ON}\\=(r_1\cos A, r_1\sin A, 0)×(-r_2\cos B, r_2\sin B, 0)\\ =(0,0,r_1r_2\cos A\sin B+r_1r_2\sin A\cos B)\end{array}\]
\[\therefore |\overrightarrow{OM}×\overrightarrow{ON}|=r_1r_2(\cos A\sin B+\sin A\cos B)\] Since $π-(A+B)$ is the angle between $OM$ and $ON$, so,
\[\begin{array}{c}\sin[π-(A+B)]=\frac{|\overrightarrow{OM}×\overrightarrow{ON}|}{|\overrightarrow{OM}| |\overrightarrow{ON}|}\\ \sin(A+B)=\frac{r_1r_2(\cos A\sin B+\sin A\cos B)}{r_1r_2}\\ \therefore \sin(A+B)=\sin A\cos B+\cos A\sin B\end{array}\]
sin(A-B)=sinAcosB-cosAsinB
Let $XOX’$ and $YOY’$ be two mutually perpendicular straight lines representing x-axis and y-axis respectively. Let $\angle XON=A$ and $\angle XOM=B$ so that $\angle MON=A-B$.

Let $OM=r_1$ and $ON=r_2$. Then, the coordinates of $M$ and $N$ are $(r_1\cos B, r_1\sin B)$ and $(r_2\cos A, r_2\sin A$ respectively.
\[\therefore\overrightarrow{OM}=(r_1\cos B, r_1\sin B, 0)\] and, \[\overrightarrow{ON}=(r_2\cos A, r_2\sin A, 0)\]
Now, \[\begin{array}{c}\overrightarrow{OM}×\overrightarrow{ON}\\=(r_1\cos B, r_1\sin B, 0)×(r_2\cos A, r_2\sin A, 0)\\=(0,0,r_1r_2\sin A\cos B-r_1r_2\cos A\sin B)\end{array}\]
\[\therefore |\overrightarrow{OM}×\overrightarrow{ON}|=r_1r_2(\sin A\cos B-\cos A\sin B)\] Since $A-B$ is the angle between $OM$ and $ON$, so,
\[\begin{array}{c}\sin(A-B)=\frac{|\overrightarrow{OM}×\overrightarrow{ON}|}{|\overrightarrow{OM}| |\overrightarrow{ON}|}\\ \sin(A-B)=\frac{r_1r_2(\sin A\cos B-\cos A\sin B)}{r_1r_2}\\ \therefore \sin(A-B)=\sin A\cos B-\cos A\sin B\end{array}\]
sinA/a=sinB/b=sinC/c
In $\Delta ABC$, let $\overrightarrow{BC}=\overrightarrow{a}$, $\overrightarrow{CA}=\overrightarrow{b}$ and $\overrightarrow{AB}=\overrightarrow{c}$.

By triangle law of vector addition, \[\overrightarrow{BC}=\overrightarrow{BA}+\overrightarrow{AC}\] \[\overrightarrow{a}=-\overrightarrow{c}-\overrightarrow{b}\text{ __(1)}\] Multiplying $\text{(1)}$ vectorially by $\overrightarrow{b}$, we get,
\[\overrightarrow{a}×\overrightarrow{b}=-\overrightarrow{c}×\overrightarrow{b}-\overrightarrow{b}×\overrightarrow{b}\] \[\therefore\overrightarrow{a}×\overrightarrow{b}=\overrightarrow{b}×\overrightarrow{c}\text{ __(2)}\]
Again, multiplying $\text{(1)}$ vectorially by $\overrightarrow{c}$, we get, \[\overrightarrow{c}×\overrightarrow{a}=-\overrightarrow{c}×\overrightarrow{c}-\overrightarrow{c}×\overrightarrow{b}\] \[\therefore\overrightarrow{c}×\overrightarrow{a}=\overrightarrow{b}×\overrightarrow{c}\text{ __(3)}\]
From $\text{(2)}$ and $\text{(3)}$, \[\overrightarrow{a}×\overrightarrow{b}=\overrightarrow{b}×\overrightarrow{c}=\overrightarrow{c}×\overrightarrow{a}\] Taking modulus, \[|\overrightarrow{a}×\overrightarrow{b}|=|\overrightarrow{b}×\overrightarrow{c}|=|\overrightarrow{c}×\overrightarrow{a}|\] \[\Rightarrow ab\sin(π-C)=bc\sin(π-A)\]\[=ca\sin(π-B)\] \[\Rightarrow ab\sin C=bc\sin A=ca\sin B\] \[\Rightarrow\frac{ab\sin C}{abc}=\frac{bc\sin A}{abc}=\frac{ca\sin B}{abc}\] \[\Rightarrow\frac{ \sin C}{c}=\frac{\sin A}{a}=\frac{\sin B}{b}\]
Therefore, in any triangle $ABC$, \[\frac{\sin A}{a}=\frac{\sin B}{b}=\frac{\sin C}{c}\]
Previous: Vector Product or Cross Product
