Products and Quotients of Complex Numbers

The polar or trigonometric form of complex numbers provides us a quick and efficient method for computing the products and quotients of complex numbers.

The product and quotient of two complex numbers \[\begin{array}{l} & z_1 &=r_1(\cos\theta_1+i\sin\theta_1) \\ \text{and}, & z_2 &= r_2(\cos\theta_2+i\sin\theta_2) \end{array}\] are given by, \[\begin{array}{l} & z_1z_2 &= r_1r_2[\cos(\theta_1+\theta_2)+i\sin(\theta_1+\theta_2)] \\ \text{and,} & \frac{z_1}{z_2} &= \frac{r_1}{r_2}[\cos(\theta_1-\theta_2)+i\sin(\theta_1-\theta_2)\end{array}\]

Proof: \[\begin{array}{l} z_1\cdot z_2 &= r_1(\cos\theta_1+i\sin\theta_1)\cdot r_2(\cos\theta_2+i\sin\theta_2) \\ &= r_1r_2(\cos\theta_1\cos\theta_2+icos\theta_1\sin\theta_2+ i\sin\theta_1\cos\theta_2+i^2\sin\theta_1\sin\theta_2) \\ &= r_1r_2 [(\cos\theta_1\cos\theta_2-\sin\theta_1\sin\theta_2)+i(\sin\theta_1\cos\theta_2+\cos\theta_1\sin\theta_2)] \\ &= r_1r_2 [\cos(\theta_1+\theta_2)+i\sin(\theta_1+\theta_2)] \end{array}\]

And, \[\begin{array}{l} \frac{z_1}{z_2} &= \frac{r_1(\cos\theta_1+i\sin\theta_1)}{r_2(\cos\theta_2+ i\sin\theta_2)} \\ &= \frac{r_1(\cos\theta_1+i\sin\theta_1)}{r_2(\cos\theta_2+ i\sin\theta_2)} × \frac{(\cos\theta_2-i\sin\theta_2)}{(\cos\theta_2-i\sin\theta_2)} \\ &= \frac{r_1}{r_2} \left[\frac{ \cos\theta_1\cos\theta_2-i\cos\theta_1\sin\theta_2+i\sin\theta_1\cos\theta_2-i^2\sin\theta_1\sin\theta_2}{\cos^2\theta_2-i^2\sin^2\theta_2}\right] \\ &= \frac{r_1}{r_2} \left[\frac{(\cos\theta_1\cos\theta_2+\sin\theta_1\sin\theta_2)+i(\sin\theta_1\cos\theta_2-\cos\theta_1\sin\theta_2)}{\cos^2\theta_2+\sin^2\theta_2}\right] \\ &= \frac{r_1}{r_2} [\cos(\theta_1-\theta_2)+i\sin(\theta_1-\theta_2)] \end{array}\]

If we introduce a third complex number in the product considered, then \[r_1(\cos\theta_1+i\sin\theta_1) \cdot r_2(\cos\theta_2+i\sin\theta_2) \cdot r_3(\cos\theta_3+i\sin\theta_3)\] \[=r_1r_2[\cos(\theta_1+\theta_2)+i\sin(\theta_1+\theta_2)]\cdot r_3(\cos\theta_3+i\sin\theta_3)\] \[=r_1r_2r_3[\cos(\theta_1+\theta_2+\theta_3)+i\sin(\theta_1+\theta_2+\theta_3)]\]

Similarly, the product of four or more complex numbers can be obtained. If there are $n$ such complex numbers, then,

\[r_1(\cos\theta_1+i\sin\theta_1)\cdot r_2(\cos\theta_2+i\sin\theta_2)…\cdot r_n(\cos\theta_n+ i\sin\theta_n)\] \[=r_1r_2…\cdot r_n[\cos(\theta_1+\theta_2+…+\theta_n)+i\sin(\theta_1+\theta_2+…+ \theta_n)]\]

This formula for the product of $n$ complex numbers gives us the value of the $n^{\text{th}}$ power of a complex number which can be stated as a theorem known as De Moivre’s Theorem.

The complex numbers \[\begin{array}{l} & z_1 &=r_1(\cos\theta_1+i\sin\theta_1) \\ \text{and,} & z_2 &= r_2(\cos\theta_2+i\sin\theta_2) \end{array}\] \[\begin{array}{l} \text{give} & |z_1|=r_1, & |z_2|=r_2 \\ \text{and,} & \text{amp}(z_1)=\theta_1, & \text{amp}(z_2)=\theta_2 \end{array}\]

Now, \[\begin{array}{l} & z_1z_2 &= r_1r_2[\cos(\theta_1+\theta_2)+i\sin(\theta_1+\theta_2)] \\ \text{gives} & |z_1z_2| &= r_1r_2=|z_1||z_2| \\ \text{and,} & \text{amp}(z_1z_2) &= \theta_1+\theta_2 = \text{amp}(z_1)+\text{amp}(z_2) \end{array}\]

Again, \[\begin{array}{l} & \frac{z_1}{z_2} &= \frac{r_1}{r_2} [\cos(\theta_1-\theta_2)+i\sin(\theta_1-\theta_2)] \\ \text{gives,} & \left|\frac{z_1}{z_2}\right| &=\frac{r_1}{r_2}=\frac{|z_1|}{|z_2|} \\ \text{and,} & \text{amp}\left(\frac{z_1}{z_2}\right) &= \theta_1-\theta_2 =\text{amp}(z_1)-\text{amp}(z_2) \end{array}\]

Geometrical Representation

The product and the quotient of two complex numbers can be represented geometrically as follows:

Let the complex numbers \[\begin{array}{l} & z_1 &= r_1(\cos\theta_1+i\sin\theta_1) \\ \text{and,} & z_2 &= r_2(\cos\theta_2+i\sin\theta_2) \end{array}\] with magnitudes $r_1$ and $r_2$ and the amplitudes $\theta_1$ and $\theta_2$ be represented in the complex plane by the points $P(r_1,\theta_1)$ and $Q(r_2,\theta_2)$ respectively.

Then, the complex number $z_1z_2$ with magnitude $r_1r_2$ and amplitude $\theta_1+\theta_2$ will be represented by the point $R$ such that $\angle XOR=\theta_1+\theta_2$ and $OR=r_1r_2$.

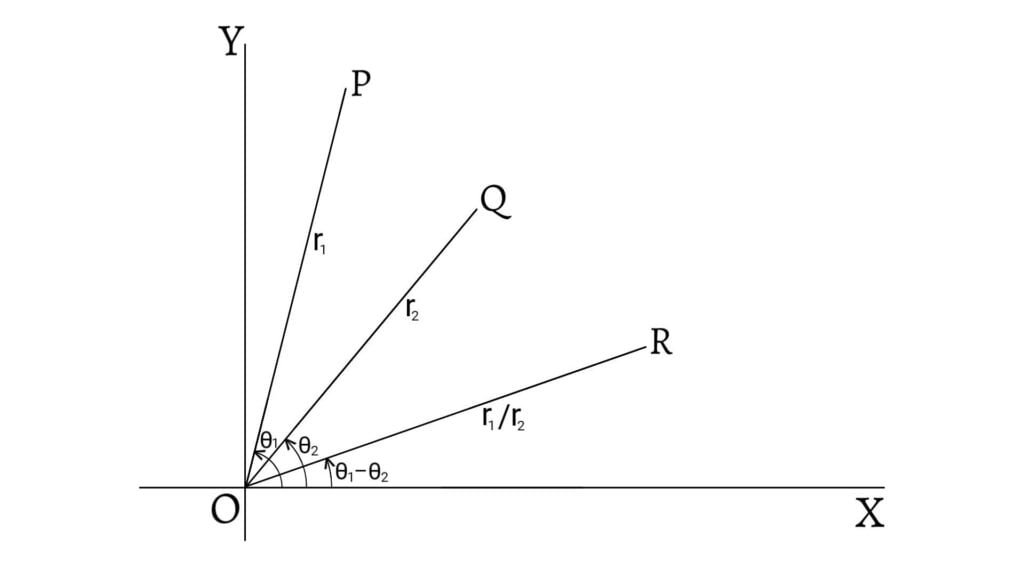
Similarly, the complex number $\frac{z_1}{z_2}$ with magnitude $\frac{r_1}{r_2}$ and amplitude $\theta_1-\theta_2$ will be represented by the point $R$ such that $\angle XOR=\theta_1-\theta_2$ and $OR=\frac{r_1}{r_2}$.