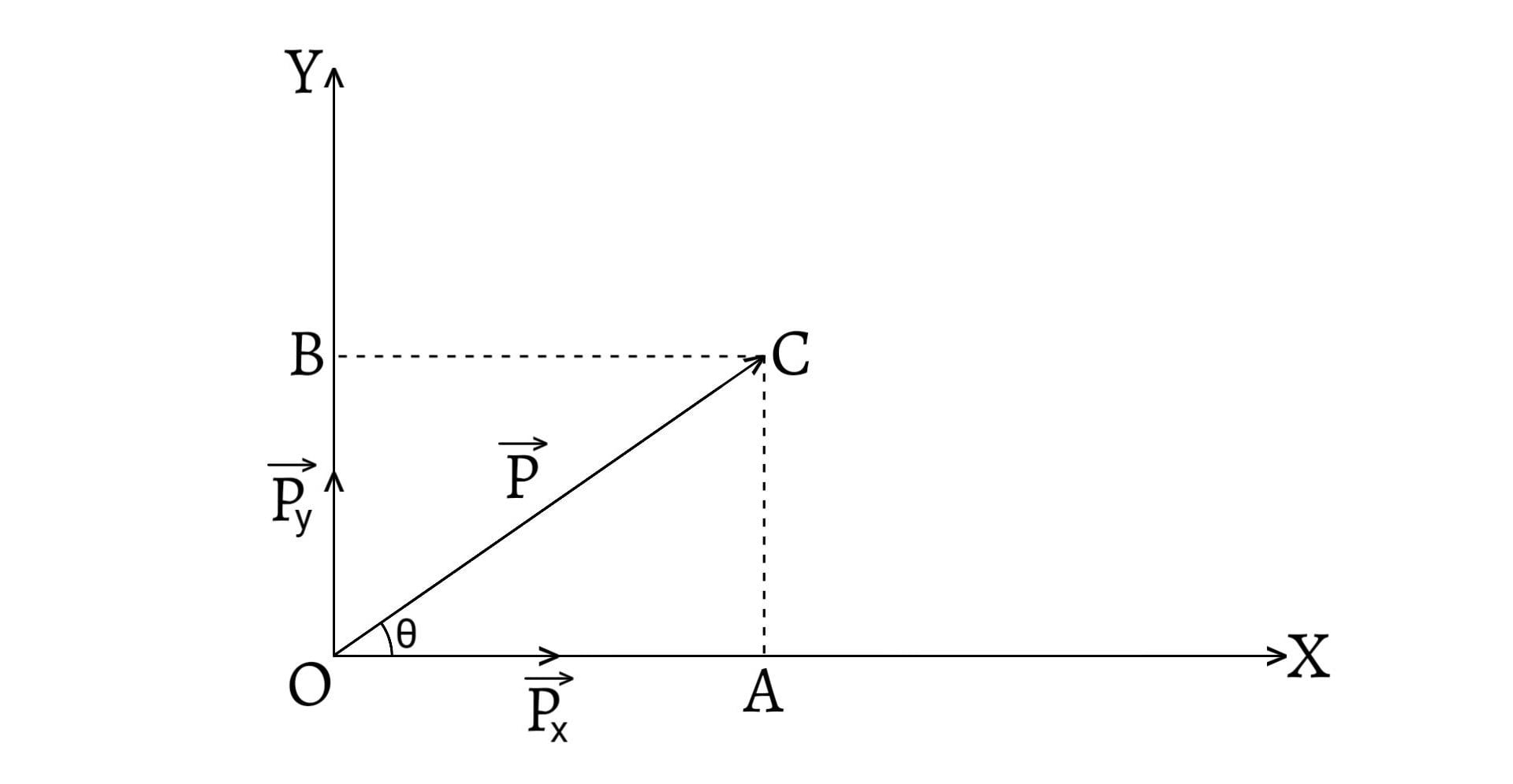
Let $O$ be the origin and let $OX$, $OY$ and $OZ$ represent x-axis, y-axis and z-axis respectively. Let $P(x,y,z)$ be a point in space. Then, \[\overrightarrow{OP}=(x,y,z)= x\:\overrightarrow{i}+ y\:\overrightarrow{j}+ z\:\overrightarrow{k}\] and the modulus of $\overrightarrow{OP}$ is given by, \[OP=|\overrightarrow{OP}|=\sqrt{x^2+y^2+z^2}\]

Let the line $\overrightarrow{OP}$ make the angles $\alpha$, $\beta$ and $\gamma$ with the three mutually perpendicular straight lines $OX$, $OY$ and $OZ$ respectively. Then, $\cos\alpha$, $\cos\beta$ and $\cos\gamma$ are said to be the direction cosines of the line $OP$. $\cos\alpha$, $\cos\beta$ and $\cos\gamma$ are denoted by $l$, $m$ and $n$ respectively.
[Learn more: Direction Cosines]
Now, \[\cos\gamma=\frac{OC}{OP}=\frac{z}{\sqrt{x^2+y^2+z^2}}\] Similarly, \[\cos\alpha=\frac{x}{ \sqrt{x^2+y^2+z^2}}\] \[\text{and,}\;\;\cos\beta=\frac{y}{\sqrt{x^2+y^2+z^2}}\]
Also, the unit vector along $\overrightarrow{OP}$ denoted by $\hat{OP}$ is defined by, \[\hat{OP}=\frac{\overrightarrow{OP}}{|\overrightarrow{OP}|}=\frac{ x\:\overrightarrow{i}+y\:\overrightarrow{j}+z\:\overrightarrow{k}}{\sqrt{x^2+y^2+z^2}}\]
\[=\frac{x}{\sqrt{x^2+y^2+z^2}}\overrightarrow{i}+\frac{y}{\sqrt{x^2+y^2+z^2}}\overrightarrow{j} +\frac{z}{\sqrt{x^2+y^2+z^2}}\overrightarrow{k}\]
Hence, the direction cosines of the line $OP$ are the coefficients of $\overrightarrow{i}$, $\overrightarrow{j}$ and $\overrightarrow{k}$ of the unit vector $\hat{OP}$. \[\therefore l=\cos\alpha =\frac{x}{\sqrt{x^2+y^2+z^2}}\] \[\therefore m=\cos\beta=\frac{y}{\sqrt{x^2+y^2+z^2}}\] \[\therefore n=\cos\gamma=\frac{z}{\sqrt{x^2+y^2+z^2}}\]
From these values of $l$, $m$, $n$, we have, \[l^2+m^2+n^2\] \[=\frac{x^2}{x^2+y^2+z^2}+\frac{ y^2}{x^2+y^2+z^2}+\frac{z^2}{x^2+y^2+z^2}\] \[=\frac{x^2+y^2+z^2}{x^2+y^2+z^2}=1\] \[\therefore l^2+m^2+n^2=1\]
Previous: Coplanar Vectors