Types of Vectors

Unit Vector

A vector whose magnitude is unity is called a unit vector. Hence, if $|\overrightarrow{OP}|=1$, then $\overrightarrow{OP}$ is said to be a unit vector. The examples of unit vectors are $(1,0)$ and $(0,1)$.

Unit vector is dimensionless and represents only direction. The unit vector of a non zero vector $\overrightarrow{A}$ in the direction of $\overrightarrow{A}$ is represented by $\hat{A}$ (read A-cap or A-hat) and is given by \[\hat{A}=\frac{\overrightarrow{A}}{|\overrightarrow{A}|}\]

Hence, if $\overrightarrow{A}=(a_1,a_2)≠0$ then the unit vector $\hat{A}$ in the direction of $\overrightarrow{A}$ is defined by \[\left(\frac{a_1}{\sqrt{a_1^2+a_2^2}},\frac{a_2}{\sqrt{a_1^2+a_2^2}}\right)\]

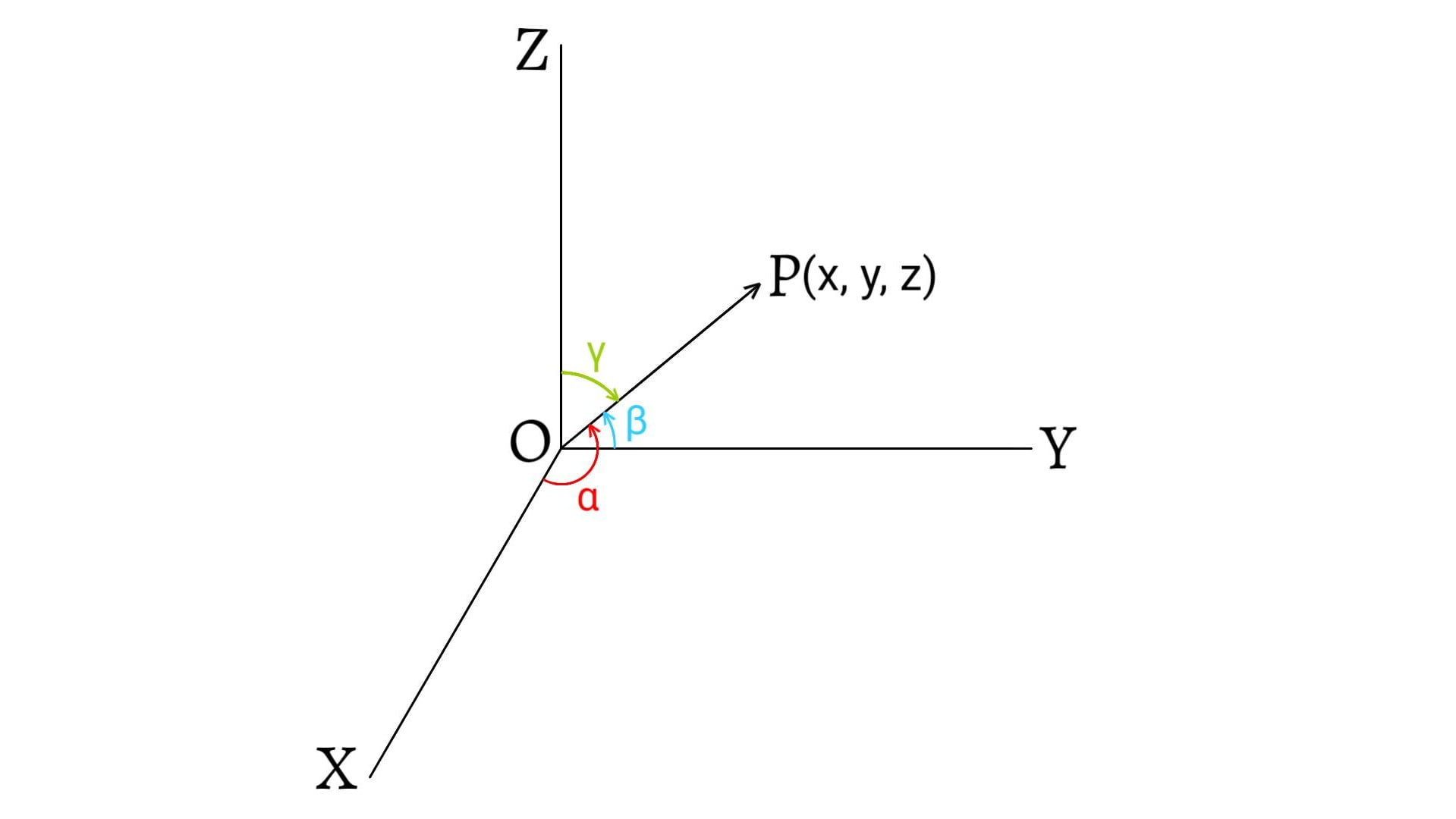
The unit vectors along X, Y and Z axes of Cartesian coordinates system are represented by $\hat{i}$, $\hat{j}$ and $\hat{k}$ respectively.

More: Unit Vector

Zero Vector (Null Vector)

A vector whose magnitude is zero is called a null vector or zero vector. So, $(0,0)$ is the zero vector and is denoted by $\overrightarrow{O}$. In a zero vector, the origin and the terminal point coincide. The direction of a zero vector is indeterminate.

More: Zero Vector (Null Vector)

Negative Vectors

Two vectors having equal magnitude but opposite directions are called negative vectors. A vector having the same magnitude as that of a given vector $\overrightarrow{OP}$ but direction opposite to it and denoted by $-\overrightarrow{OP}$ or $\overrightarrow{PO}$ is called the negative of $\overrightarrow{OP}$.

Co-initial Vectors

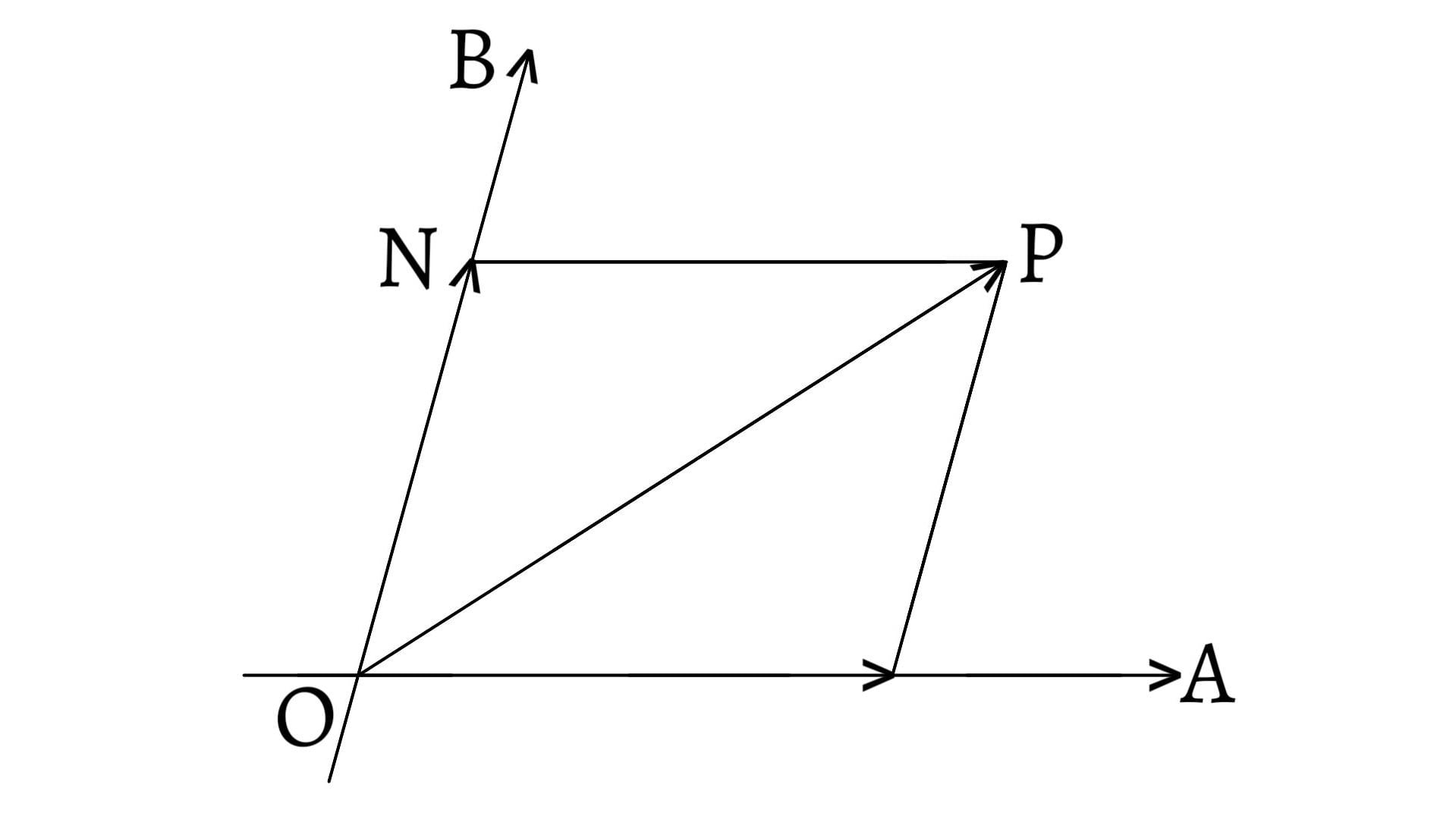
The vectors starting from a common initial point are said to be co-initial vectors. In the figure given below, $\overrightarrow{A}$ and $\overrightarrow{B}$ start from a same initial point $O$. Hence, $\overrightarrow{A}$ and $\overrightarrow{B}$ are co-initial vectors.

Collinear Vectors

If two vectors are parallel to each other whatever may be their magnitudes, then they are called collinear vectors. In other words, if angle between two vectors is $0°$ or $180°$, then the vectors are said to be collinear. Collinear vectors are further divided into like and unlike vectors.

Like Vectors

Two vectors are said to be like if they have the same direction whatever may be their magnitudes.

Unlike Vectors

Two vectors are said to be unlike if they have opposite directions whatever may be their magnitudes. So, if $\overrightarrow{AB}=-2\overrightarrow{CD}$, then $\overrightarrow{AB}$ and $\overrightarrow{CD}$ are unlike vectors.

More: Collinear Vectors

Orthogonal Vectors

Vectors perpendicular to each other are called orthogonal vectors. In particular case, unit vectors $\hat{i}$, $\hat{j}$ and $\hat{k}$ along X, Y and Z axes are mutually perpendicular.

Equal Vectors

Two vectors having equal magnitude and same direction are called equal vectors. If $\overrightarrow{A}$ and $\overrightarrow{B}$ have equal magnitude and same direction. Hence, they are equal vectors; $\overrightarrow{A}=\overrightarrow{B}$.

Position Vector

The vector representing the position of an object relative to an arbitrary origin is called the position vector. If $O$ is arbitrary origin and $P(x,y,z)$ is the position of a particle, then the position vector of particle $P$ relative to origin $O$ is given by \[\overrightarrow{OP}=(x,y,z)\]

Know more: Position Vectors

Localised Vector

A vector which passes through a given point and which is parallel to the given vector is said to be a localised vector.

Also, we may write a localised vector $\overrightarrow{AB}$ as an ordered pair $(x,y)$ by accepting the following principle of parallel displacement.

‘Any vector starting from a point may be displaced to any other point so long as its magnitude and direction remain unaltered.‘ Such an ordered pair $(x,y)$ represents a position vector equivalent to the given localised vector $\overrightarrow{AB}$.