Let $AB:x\cos\alpha+y\sin\alpha=p$ [Normal Form] be the given line and $P(x_1,y_1)$ be the given point. Also, let $PM\perp AB$ and $ON\perp AB$ such that the perpendicular distance from the origin on the line is $p$ i.e. $ON=p$. Then, we have to find $PM$. For this, through $P$, draw $A’B’//AB$ and produce $ON$ upto $ON’$ so that $ON’=p’$.
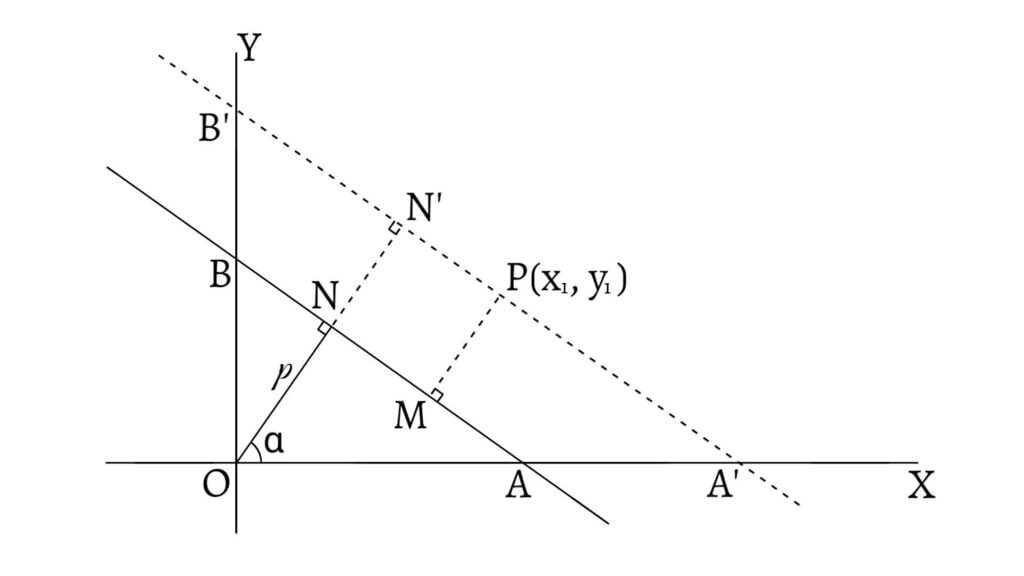
\[PM=N’N=ON’-ON=p’-p\] Equation of $A’B’$ is, \[x\cos\alpha+y\sin\alpha=p’\] Since this line passes through $P(x_1,y_1)$, so, \[x_1\cos\alpha+y_1\sin\alpha=p’\] \[\therefore PM=\pm(p’-p)\] \[PM=\pm(x_1\cos\alpha+y_1\sin\alpha-p)\]
Now, we find the perpendicular distance drawn from the point $P(x_1,y_1)$ on the line whose equation is $Ax+By+C=0$. For that, we reduce the equation $Ax+By+C=0$ into normal form.
If $C>0$, \[p=\frac{C}{\sqrt{A^2+B^2}},\text{ }\cos\alpha=\frac{-A}{\sqrt{A^2+B^2}}\]\[\text{ and, }\sin\alpha=\frac{-B}{\sqrt{A^2+B^2}}\] If $C<0$, \[p=\frac{-C}{\sqrt{A^2+B^2}},\text{ }\cos\alpha=\frac{A}{\sqrt{A^2-B^2}}\]\[\text{ and, }\sin\alpha=\frac{B}{\sqrt{A^2+B^2}}\] [From: Reduction of Linear Equation into Normal Form (Linear Equation $Ax+By+C=0$)]
For both the cases, the perpendicular distance from the point $(x_1,y_1)$ on the line $x\cos\alpha+y\sin\alpha=p$ is \[PM=\pm(x_1\cos\alpha+y_1\sin\alpha-p)\] \[=\pm\left(x_1\frac{A}{\sqrt{A^2+B^2}}+y_1\frac{B}{\sqrt{A^2+B^2}}+\frac{C}{\sqrt{A^2+B^2}}\right)\] \[=\pm\left(\frac{Ax_1+By_1+C}{\sqrt{A^2+B^2}}\right)\] \[=\left|\frac{Ax_1+By_1+C}{\sqrt{A^2+B^2}}\right|\]
Alternative Method
Reduce the given line $Ax+By+C=0$ into the double intercept form, \[\frac{x}{\left(-\frac{C}{A}\right)}+\frac{y}{\left(-\frac{C}{B}\right)}=1\] [From: Reduction of Linear Equation into the Double Intercept Form (Linear Equation $Ax+By+C=0$)]
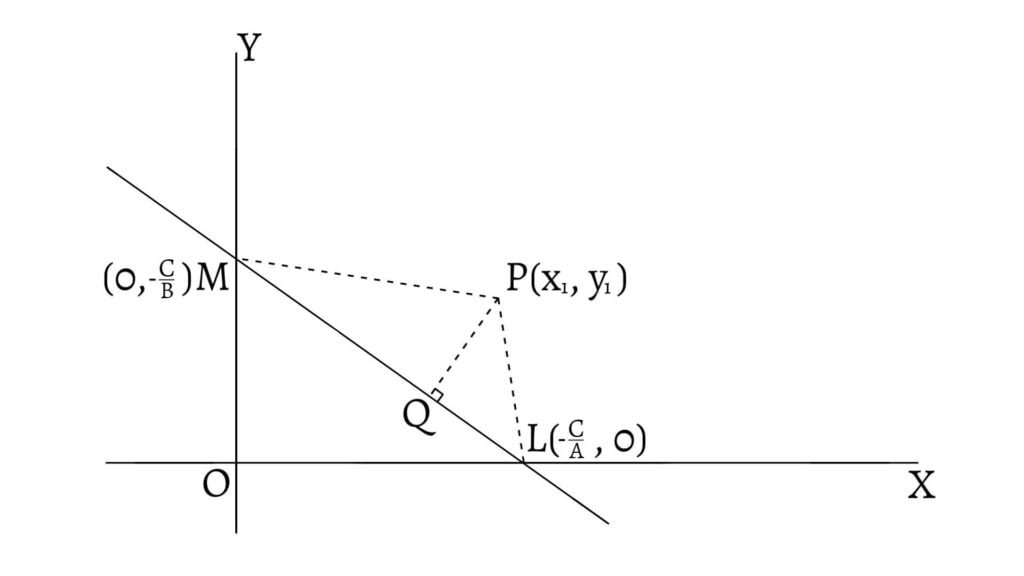
Let the given line meet the axes in $L$ and $M$ so that the coordinates of $L$ and $M$ are $\left(-\frac{C}{A},0\right)$ and $\left(0,-\frac{C}{B}\right)$. Let $PQ$ be the perpendicular distance from $P(x_1,y_1)$ on $LM$. Join $LP$ and $MP$. \[\therefore\text{Area of }\Delta LMP\] \[=\frac{1}{2}\left|x_1\left(0+\frac{C}{B}\right)+\frac{-C}{B}\left(-\frac{C}{B}-y_1\right)+0(y_1-0)\right|\] \[=\frac{1}{2}\left|\frac{Cx_1}{B}+\frac{C^2}{AB}+\frac{Cy_1}{A}\right|\] \[=\frac{1}{2}\left|\frac{C}{AB}(Ax_1+By_1+C)\right|\] \[=\frac{1}{2}\left|\frac{C}{AB}\right|\left|Ax_1+By_1+C\right|\]
Also, \[\text{Area of }\Delta LMP=\frac{1}{2}LM.PQ\] \[=\frac{1}{2}\sqrt{\left(0+\frac{C}{A}\right)^2+\left(-\frac{C}{B}-0\right)^2}.PQ\] \[=\frac{1}{2}\sqrt{\frac{C^2(A^2+B^2)}{A^2B^2}}.PQ\] \[=\frac{1}{2}\left|\frac{C}{AB}\right|\sqrt{A^2+B^2}.PQ\]
\[\therefore\Delta LMP=\frac{1}{2}\left|\frac{C}{AB}\right|\sqrt{A^2+B^2}.PQ\] \[=\frac{1}{2}\left|\frac{C}{AB}\right| \left|Ax_1+By_1+C\right|\] \[\text{or, }PQ=\frac{|Ax_1+By_1+C|}{\sqrt{A^2+B^2}}=\left|\frac{Ax_1+By_1+C}{\sqrt{A^2+B^2}}\right|\] Thus, the perpendicular distance from $(x_1,y_1)$ on the line $Ax+By+C=0$ is \[\left|\frac{Ax_1+By_1+C}{\sqrt{A^2+B^2}}\right|\]
Find the length of perpendicular drawn from $(2,3)$ to the line $8x+15y+24=0$.
Given line is, \[8x+15y+24=0\] Perpendicular distance of the given line from $(2,3)$ is, \[\pm\left(\frac{8×2+15×3+24}{\sqrt{8^2+15^2}}\right)=\pm\frac{85}{17}=5\text{ units}\]
If $p$ is the length of the perpendicular dropped from the origin on the line $\frac{x}{a}+\frac{y}{b}=1$, prove that $\frac{1}{a^2}+\frac{1}{b^2}=\frac{1}{p^2}$.
Given line is, \[\frac{x}{a}+\frac{y}{b}=1\] \[bx+ay-ab=0\] Perpendicular distance of the given line from origin is, \[p=\pm\left(\frac{b×0+a×0-ab}{\sqrt{b^2+a^2}}\right)=\pm\frac{ab}{\sqrt{a^2+b^2}}\] \[p^2=\frac{a^2b^2}{a^2+b^2}\] \[\frac{1}{p^2}=\frac{a^2+b^2}{a^2b^2}\] \[\therefore\frac{1}{a^2}+\frac{1}{b^2}=\frac{1}{p^2}\]
Find the distance between the parallel lines $2x-5y-6=0$ and $6x-15y+11=0$.
Given lines are, \[2x-5y-6=0\] \[6x-15y+11=0\] Put $x=3$ in $2x-5y-6=0$, then, \[2×3-5y-6=0\] \[\therefore y=0\] Hence, $(3,0)$ is a point on the line $2x-5y-6=0$. Thus, perpendicular distance from $(3,0)$ on the line $6x-15y+11=0$ is, \[\pm\left(\frac{6×3-15×0+11}{\sqrt{6^2+15^2}}\right)=\pm\frac{29}{\sqrt{261}}=\frac{29}{\sqrt{261}}\text{ units}\]
What are the points on the axis of x whose perpendicular distance from the straight line $\frac{x}{a}+\frac{y}{b}=1$ is a?
Let $P(h,0)$ be the point on x-axis. Given line is, \[\frac{x}{a}+\frac{y}{b}=1\] \[bx+ay-ab=0\] Perpendicular distance of the given line from $P$ is, \[a=\pm\left(\frac{bh+a×0-ab}{\sqrt{b^2+a^2}}\right)\] \[a=\pm\frac{bh-ab}{\sqrt{a^2+b^2}}\] \[\frac{a}{b}\sqrt{a^2+b^2}=\pm(h-a)\] \[\therefore\frac{a}{b}\sqrt{a^2+b^2}=h-a\text{ and }\frac{a}{b}\sqrt{a^2+b^2}=-h+a\] \[h=\frac{a}{b}\sqrt{a^2+b^2}+a\text{ or }h=a-\frac{a}{b}\sqrt{a^2+b^2}\] Thus, the points on the x-axis are, \[\left(\frac{a}{b}\sqrt{a^2+b^2}+a,0\right)\text{ and }\left(a-\frac{a}{b}\sqrt{a^2+b^2},0\right)\]
Find the equation of the line which is at right angles to $3x+4y=12$, such that its perpendicular distance from the origin is equal to the length of the perpendicular from $(3,2)$ on the given line.
Given line is, \[3x+4y-12=0\] Its perpendicular distance from $(3,2)$ is, \[\pm\left(\frac{3×3+4×2-12}{\sqrt{9+16}}\right)=\pm\frac{5}{5}=1\] and, \[\text{Slope of the given line}=-\frac{3}{4}\] Since the required line is perpendicular to the given line, so, \[\text{Slope of the required line }(m)=\frac{4}{3}\] Equation of the required line is given by, \[y=mx+c\] \[y=\frac{4}{3}x+c\] \[4x-3y+3c=0\] Its perpendicular distance from the origin is, \[1=\pm\left(\frac{4×0-3×0+3c}{\sqrt{16+9}}\right)\] \[1=\pm\frac{3c}{5}\] \[\therefore c=\pm\frac{5}{3}\] Thus, required equation of line is, \[4x-3y\pm 5=0\]
Previous: The Two Sides of a Line
