Induced Electric Fields

Whenever there is change in the magnetic flux, an emf is induced in a conductor. Hence, an emf can be induced in a conductor by changing the magnetic flux directly or by moving the conductor in a magnetic field.

Consider a long thin solenoid having $n$ number of turns per unit length and area of cross section $A$. Let the solenoid be encircled at its centre by a circular conducting loop. Current in the loop is measured by using a galvanometer.

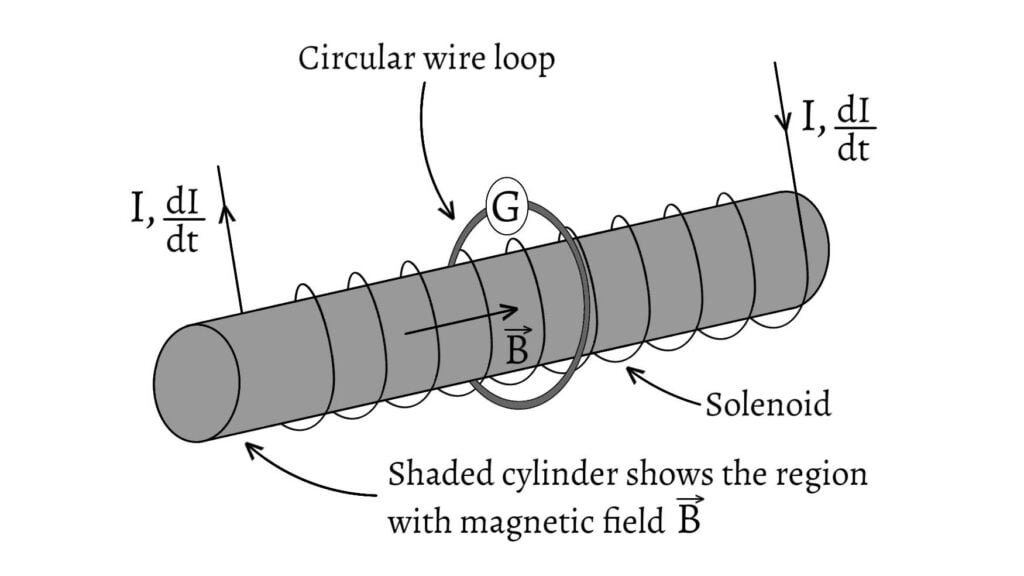
When current $I$ passes through the solenoid, the magnetic field $B$ inside the solenoid is given by \[B=\mu_0nI\] If we neglect the small field outside the solenoid and take area vector $\overrightarrow{A}$ in the same direction as $\overrightarrow{B}$, then magnetic flux through the loop is given by \[\phi=BA=\mu_0nIA\]

From Faraday’s laws of electromagnetic induction, the induced emf in the loop is given by \[\varepsilon=-\frac{d\phi}{dt}\text{ __(1)}\] \[\varepsilon=-\mu_0nA\frac{dI}{dt}\] Let the total resistance of the loop be $R$, then the induced current in the loop is given by \[\text{Induced current}=\frac{\varepsilon}{R}\]

A force makes the charges to move around the loop. Since emf is induced, it means that work is done on the charges in the loop. But the source of this work cannot be the batteries since there is not any battery connected in the loop. The source of this work also cannot be the magnetic field because Lorentz force does no work on moving charges. It makes us to conclude that there has to be an induced electric field in the loop caused by the change in magnetic flux. The change in magnetic flux acts as a source of electric field.

The total work done $(W)$ on a charge $q$ by the electric field when the charge goes once around the loop is given by \[W=q\varepsilon\]

Hence, the work done by the induced electric field $\overrightarrow{E}$ per unit charge is equal to the induced emf $\varepsilon$.

\[\therefore\oint\overrightarrow{E}.\overrightarrow{dl}=\varepsilon\text{ __(2)}\] where $\oint$ represents the line integral around the circuit.

The electric field in the loop is not conservative because line integral of $\overrightarrow{E}$ around a closed path is not zero. \[\oint\overrightarrow{E}.\overrightarrow{dl}≠0\]

This is a difference between induced electric fields and electrostatic fields. An electrostatic field is conservative and hence the line integral of electrostatic field around a closed path is zero. \[\oint\overrightarrow{E}.\overrightarrow{dl}=0\]

From equation $\text{(1)}$ and $\text{(2)}$, \[\oint\overrightarrow{E}.\overrightarrow{dl}=-\frac{d\phi}{dt}\]

This equation is true only when the path around which we integrate is stationary.

Magnitude of Induced Electric Fields

To find the magnitude of an induced electric field, let us consider the stationary circular loop of radius $r$. Because of the symmetrical shape of cylinder, the electric field $\overrightarrow{E}$ has the same magnitude at every point on the circle and is tangent to it at each point.

Hence, the line integral of induced electric field becomes,

\[\oint\overrightarrow{E}.\overrightarrow{dl}=2πrE\] \[-\frac{d\phi}{dt}=2πrE\] \[E=\frac{1}{2πr}\left|\frac{d\phi}{dt}\right|\]

Here, $E$ is the magnitude of the induced electric field.

---

---