The phenomenon of the production of induced emf in a secondary coil as a result of change of current or magnetic flux in primary coil is known as mutual induction.
Consider two coils $P$ (primary) and $S$ (secondary). The coil $P$ is connected with a battery, a rheostat and a key. The coil $S$ is connected with a galvanometer. These two coils are placed close to each other as shown in the figure given below.
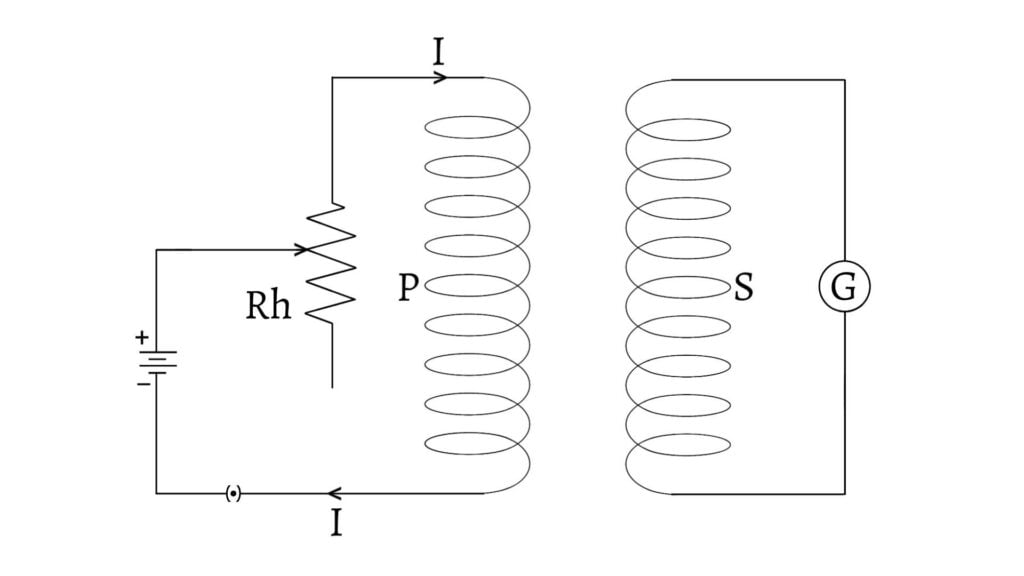
When the current is increased in the primary coil, the magnetic field around $P$ also increases. As a result, magnetic flux linking with secondary coil also changes. Hence, an emf is induced in the secondary coil and an induced current flows through the secondary coil which is detected by the galvanometer.
In this way, we see that whenever the current in the primary coil changes, an induced emf is set up in the secondary coil. This phenomenon of production of induced emf in the secondary coil due to the change of magnetic flux in the primary coil is called mutual induction.
Coefficient of Mutual Induction or Mutual Inductance
Let $I_p$ be the current flowing in the primary coil and $\phi_s$ be the magnetic flux linked with the secondary coil due to primary current. It is found that the magnetic flux $(\phi_s)$ linked with the secondary coil is directly proportional to the current flowing through the primary coil.
\[\text{i.e. }\phi_s∝I_p\]
\[\phi_s=MI_p\]
where, $M$ is a proportionality constant called coefficient of mutual induction or mutual inductance. Its value depends upon the number of turns in each coil, geometrical shape and size of each coil, separation between coils, permeability of the core material and orientation of two coils. \[M=\frac{\phi_s}{I_p}\]
Thus, mutual inductance of two coils is defined as the total magnetic flux linked with secondary coil when a unit current passes through primary coil.
From Faraday’s laws of electromagnetic induction,
\[\varepsilon=-\frac{d\phi_s}{dt}=-\frac{d}{dt}(MI_p)\]
\[\therefore\varepsilon=-M\frac{dI_p}{dt}\]
where, $\frac{dI_p}{dt}$ is the rate of change of current in the primary coil.
If $\frac{dI_p}{dt}=1$, then $\varepsilon=-M$. Hence, mutual inductance of two coils can also be defined as the induced emf produced in the secondary coil due to unit rate of change of current in the primary coil. The SI unit of mutual inductance is henry $\text{(H)}$.
If $\varepsilon=1\text{ V}$ and $\frac{dI_p}{dt}=1\text{ A s}^{-1}$, then $M=1\text{ H}$. So, mutual inductance of two coils is said to be of one henry if a rate of change of current of one ampere per second in primary coil induce an emf of one volt in secondary coil.
Mutual Inductance of Two Long Coaxial Solenoids
Consider two solenoids $S_1$ and $S_2$ having turns $N_1$ and $N_2$ and each having length $l$. The solenoid $S_2$ completely surrounds the solenoid $S_1$. The two solenoids are so closely wound that they both have nearly same area of cross section $A$.
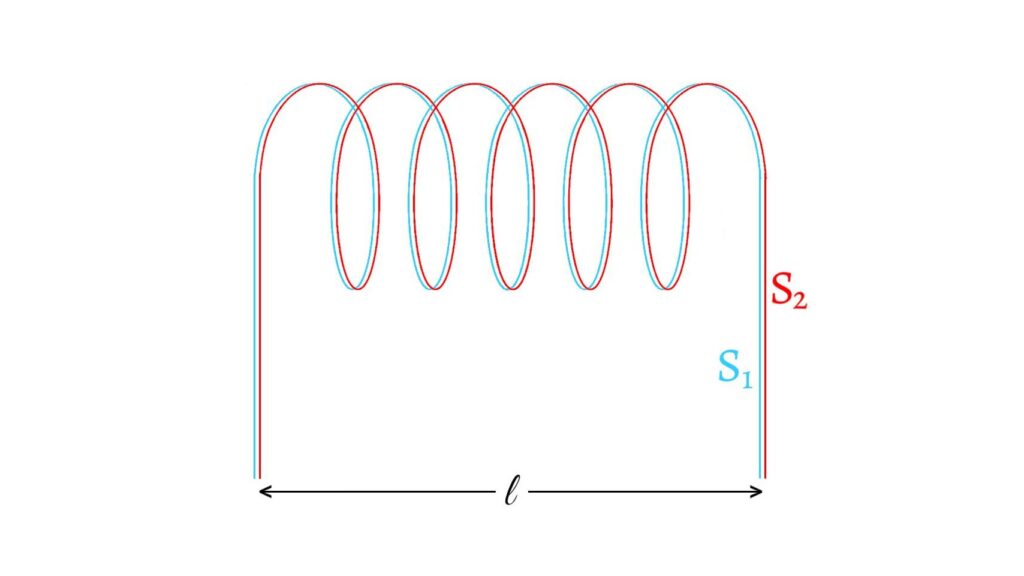
Let current $I_1$ flows through the solenoid $S_1$. Then the magnetic field inside the solenoid $S_1$ is given by
\[B_1=\mu_0n_1I_1=\mu_0\frac{N_1}{l}I_1\]
The total magnetic flux linked with solenoid $S_2$ is
\[\phi_2=N_2B_1A=\frac{\mu_0N_1N_2AI_1}{l}\]
Now, mutual inductance of the solenoids is given by
\[M=\frac{\phi_2}{I_1}=\frac{\mu_0N_1N_2A}{l}\]
This is the required expression for mutual inductance of two solenoids.
Previous: Self Induction
