OR: Prove that the range of a projectile is the same at angles θ and 90°-θ.
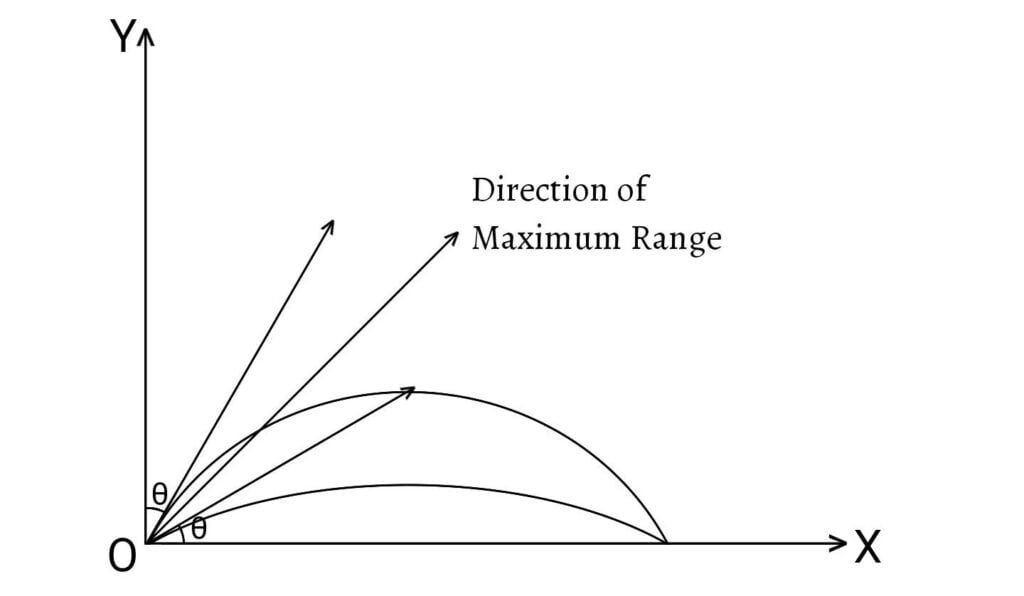
Let $u$ be the velocity of projection, $R$ be the horizontal range and $θ$ be the angle of projection. Then, \[R=\frac{u^2}{g}\sin 2θ\] \[R=\frac{u^2}{g}\sin(π-2θ)\] \[∴R=\frac{u^2}{g}\sin 2\left(\frac{π}{2}-θ\right)\] i.e. the value of the range remains same if $θ$ is replaced by $\frac{π}{2}-θ$.
Moreover, these two directions are equally inclined to the horizontal and vertical axes respectively. Hence, the direction of maximum range $(45°)$ bisects the angle between these two directions.
[Read: Projectile Motion]
A projectile fired at an angle of 18° has certain horizontal range. State another angle of projection for the same horizontal range.
The horizontal range is same for angle of projections $\theta$ and $90°-\theta$.
Here, \[\theta=18°\] and \[90°-\theta=90°-18°=72°\]
Therefore, the required another angle of projection is $72°.$
